زاوية مجسمة

زاوية مجسمة
معلومات عامة
التعريف الرياضي
[1] عدل القيمة على Wikidata
نظام الوحدات الدولي
التحليل البعدي
عدل القيمة على Wikidata

تعديل - تعديل مصدري - تعديل ويكي بياناتحول القالب

تمثيل رسومي لدرجة 1 ستراديان

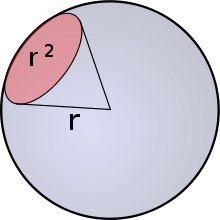
الزَاوِيَة المُجَسَّمَة[5] هي زاوية في الفضاء الثلاثي الأبعاد، تقيس الحجم الظاهري لجسم من قبل مراقب من نقطة معينة في الفضاء.[6][7][8] فجسم فراغي صغير قريب قد يبدو بحجم جسم كبير بعيد من الناظر. الزاوية الصلبة تتناسب مع مساحة السطح S، لمسقط الجسم على كرة متمركزة عند نقطة المراقبة، مقسومة على مربع شعاع تلك الكرة، R، بالعلاقة:

Ω = k S/R2

حيث:

  • Ω هي الزاوية الصلبة
  • S مساحة سطح مسقط الجسم على كرة متمركزة عن نقطة المراقبة (مساحة قاعدة المخروط)
  • R نصف قطر الكرة
  • k عامل تناسب.

علاقة الزاوية الصلبة بسطح الكرة، مشابهة لعلاقة الزاوية بمحيط الدائرة. كل الاختلاف ينحصر في كون الزاوية العادية مسطحة، أما الزاوية الصلبة فهي فراغية.

إذا اختير عامل التناسب مساويًا للواحد، تكون عندها وحدة الزاوية الصلبة وفق النظام الدولي للوحدات هي ستراديان وتختصر (sr). وهكذا تكون الزاوية الصلبة لكرة مقاسة من نقطة في داخلها هو 4π sr، والزاوية الصلبة الناتجة في مركز مكعب بالنسبة لأحد أضلاعه هي سدس هذه القيمة أي 2π/3 sr.

مراجع

  1. ^ مذكور في: ISO 80000-3:2006 Quantities and units — Part 3: Space and time. قسم أو آية أو فقرة أو بند: 3-6. الناشر: المنظمة الدولية للمعايير. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 1 مارس 2006.
  2. ^ ا ب مذكور في: ISO 80000-3:2019 Quantities and units — Part 3: Space and time. قسم أو آية أو فقرة أو بند: 3-8. الناشر: المنظمة الدولية للمعايير. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: أكتوبر 2019.
  3. ^ مذكور في: SI Brochure (9th edition): Concise summary. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 2019.
  4. ^ مذكور في: ISO 80000-3:2006 Quantities and units — Part 3: Space and time. قسم أو آية أو فقرة أو بند: 3-6.a. الناشر: المنظمة الدولية للمعايير. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 1 مارس 2006.
  5. ^ منير البعلبكي؛ رمزي البعلبكي (2008). المورد الحديث: قاموس إنكليزي عربي (بالعربية والإنجليزية) (ط. 1). بيروت: دار العلم للملايين. ص. 1110. ISBN:978-9953-63-541-5. OCLC:405515532. OL:50197876M. QID:Q112315598.
  6. ^ Beck، M.؛ Robins، S.؛ Sam، S. V. (2010). "Positivity theorems for solid-angle polynomials". Contributions to Algebra and Geometry. ج. 51 ع. 2: 493–507. arXiv:0906.4031. Bibcode:2009arXiv0906.4031B.
  7. ^ Jackson، FM (1993). "Polytopes in Euclidean n-space". Bulletin. Institute of Mathematics and its Applications. ج. 29 ع. 11/12: 172–174. مؤرشف من الأصل في 2019-02-28.
  8. ^ Eriksson، Folke (1990). "On the measure of solid angles". Math. Mag. ج. 63 ع. 3: 184–187. DOI:10.2307/2691141.

انظر أيضا

في كومنز صور وملفات عن Solid angle.