বৃত্ত

ৱিকিপিডিয়াৰ গুণগত মান বজাই ৰাখিবলৈ এই প্ৰবন্ধৰ অধিক উন্নয়নৰ থল থকা যেন অনুভৱ হয়  (বিশদ নিৰ্দেশনা চাওক)। সম্ভৱ হ'লে অনুগ্ৰহ কৰি এই প্ৰবন্ধৰ মান উন্নয়নত আপুনিও যথাসম্ভব সহায় কৰক। আলোচনা পৃষ্ঠাত অধিক তথ্য থাকিব পাৰে, চাই লয় যেন।

বৃত্ত
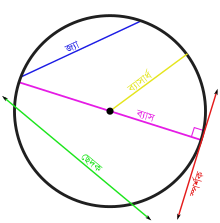জ্যা, ব্যাস, ব্যাসাৰ্ধ, স্পৰ্শক আৰু ছেদক
ক্ষেত্ৰফল	π r2 (য’ত r = ব্যাসাৰ্ধ)

ইউক্লিডীয় জ্যামিতিত, এটা স্থিৰ বিন্দুৰপৰা(কেন্দ্ৰ) এক নিৰ্দিষ্ট দূৰত্বত (ব্যাসাৰ্ধ) একেই সমতলত অৱস্থিত বিন্দুবোৰৰ গতিপথকে (ল'কাচ) বৃত্ত (ইংৰাজী: Circle) বোলা হয়।

বৃত্তৰ ওপৰত অৱস্থিত যিকোনো দুটি বিন্দুৰ সংযোগকাৰী সৰলৰেখাংশকে জ্যা বোলা হয়। বৃত্তৰ কেন্দ্ৰগামী যিকোনো জ্যাকে তাৰ ব্যাস বোলা হয়। বৃত্তৰ ব্যাস হ’ল তাৰ দীৰ্ঘতম জ্যা। ব্যাসৰ দৈৰ্ঘ্য ব্যাসাৰ্ধৰ দুগুন হয়।

বৃত্তৰ সীমাক পৰিধি বোলা হয় আৰু পৰিধিৰ অংশক বৃত্তচাপ বোলা হয়।

এটি পুৰনা জ্যোতিৰ্বিদ্যা অঙ্কন

The compass in this 13th century manuscript is a symbol of God's act of Creation. Notice also the circular shape of the halo

লিখিত ইতিহাস সংৰক্ষণ আৰম্ভ হোৱাৰ আগলৈকে বৃত্ত সম্পৰ্কে মানুহৰ ধাৰণা আছিল চকা, যি মানৱ সভ্যতাৰ অগ্ৰগতিত ব্যাপক অৱদান আগবঢ়াইছে, বৃত্তাকাৰ। গণিতত বৃত্তৰ অধ্যয়ন পৰবৰ্তী জ্যামিতি আৰু কেলকুলাছৰ দৰে উচ্চতৰ শাখাবোৰৰ উন্নয়নত অৱদান আগবঢ়াইছে। বৃত্তৰ ইতিহাসত কেইটিমান গুৰুত্বপূৰ্ণ ঘটনা হল :

• ১৭০০ খৃষ্টপূৰ্ব - ৰাইণ্ড প্যাপিৰাছে বৃত্তৰ ক্ষেত্ৰফল নিৰ্নয়ৰ এটি পদ্ধতি লিপিৱদ্ধ হয়। তাতেই ২৫৬/৮১ ক π ৰ মান ধৰা হয়।
• ৩০০ খৃষ্টপূৰ্ব - ইউক্লিডৰ এলিমেণ্টছৰ তৃতীয় গ্ৰন্থত বৃত্তৰ বৈশিষ্ট্য সমূহৰ বিষয়ে বিস্তাৰিত আলোচনা কৰা হয়।
• ১৮৮০ - লিণ্ডেমানে প্ৰমাণ কৰে যে π এটি transcendental সংখ্যা। ইয়াৰ ফলত হাজাৰ বছৰ ধৰি চলি অহা বৃত্তক বৰ্গ ৰূপান্তৰৰ সমস্যাটিৰ সমিধান ঘটে।

• বৃত্ত হল নিৰ্দিষ্ট পৰিসীমাৰ মধ্যত আৱদ্ধ বৃহত্তম ক্ষেত্ৰফল।
• বৃত্ত বিশেষ ধৰণৰ প্ৰতিসাম্যৰ অধিকাৰী এক আকৃতি। কেন্দ্ৰগামী যিকোনো ৰেখাই প্ৰতিফলন প্ৰতিসম অক্ষ হিচাপে কাম কৰে আৰু কেন্দ্ৰৰ সাপেক্ষে যিকোনো কোণত ঘূৰ্নণ প্ৰতিসাম্য তৈয়াৰ হয়।
• প্ৰতিটো বৃত্তৰ আকৃতি অভিন্ন।
• বৃত্তৰ পৰিধি আৰু ব্যাসৰ অনুপাত একটি ধ্ৰুৱ সংখ্যা, ইয়াক π দ্বাৰা প্ৰকাশ কৰা হয়।
• কাৰ্তেছীয় স্থানাঙ্ক ব্যাৱস্থাত মূলবিন্দুত কেন্দ্ৰ বিশিষ্ট একক ব্যাসাৰ্ধৰ বৃত্তক "একক বৃত্ত" বোলা হয়।

Arc, sector, and segment

বৃত্তৰ ক্ষেত্ৰফল = π × ছাঁ কৰা বৰ্গৰ ক্ষেত্ৰফল

x-y কাৰ্তেছীয় স্থানাঙ্ক ব্যাৱস্থাত, (a, b) কেন্দ্ৰ আৰু r ব্যাসাৰ্ধৰ বিশিষ্ট বৃত্তৰ সমীকৰণ হ’ল :

${\displaystyle \left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}.}$

বৃত্তস্থঃ যিকোনো বিন্দুৰ ওপৰত পাইথাগোৰাছৰ উপপাদ্য প্ৰয়োগ কৰি বৃত্তৰ এই সমীকৰণটো পোৱা যায়। মূলবিন্দুত কেন্দ্ৰ হ’লে সমীকৰণটো হ’ব :

${\displaystyle x^{2}+y^{2}=r^{2}.\!\ }$

পৰিমিতিত সমীকৰণ ৰূপান্তৰ কৰিলে :

${\displaystyle x=a+r\,\cos t,\,\!}$

${\displaystyle y=b+r\,\sin t\,\!}$

বৃত্তৰ স্পৰ্শক হৈছে এডাল ৰেখা, যি বৃত্তটোক মাত্ৰ এটা বিন্দুত স্পৰ্শ কৰে।^[1]স্পৰ্শক শব্দটো লেটিন ভাষাৰ শব্দ 'tangere' শব্দৰ পৰা আহিছে, যাৰ অৰ্থ হৈছে স্পৰ্শ কৰা আৰু ইয়াক প্ৰথমে ডেনিছ গণিতজ্ঞ থমাছ ফিনেকে ১৫৮৩ চনত ব্যৱহাৰ কৰিছিল। বৃত্ত আৰু স্পৰ্শকৰে উমৈহতীয়া বিন্দুটোক স্পৰ্শ বিন্দু বোলে।

বৃত্ত আৰু স্পৰ্শক সম্পৰ্কীয় কেতবোৰ উপপাদ্য হৈছে-

১) এটা বৃত্তৰ যিকোনো বিন্দুত টনা স্পৰ্শকডাল স্পৰ্শবিন্দুৰ মাজেৰে যোৱা ব্যাসাৰ্ধৰ লম্ব।

২) এটা বৰ্হিঃ বিন্দুৰ পৰা বৃত্তলৈ টনা স্পৰ্শকবোৰৰ দৈঘ্য সমান।

৩)দুটা ঐক্যকেন্দ্ৰিক বৃত্তত, ডাঙৰ বৃত্তটোৰ জ্যা ডালে সৰু বৃত্তটোক স্পৰ্শ কৰিলে জ্যাডাল স্পৰ্শবিন্দুত সমখণ্ডিত হয়।

জ্যামিতিত বৃত্তৰ ব্যাস হ’ল এডাল কেন্দ্ৰগামী সৰলৰেখা যাৰ প্ৰান্তবিন্দু দুটা পৰিধিৰ সৈতে সংযুক্ত হৈ থাকে। এই সৰলৰেখাৰ দৈৰ্ঘ্যকেই ব্যাস বোলা হয়। কোনো বৃত্তৰ সকলো ব্যাস সমান আৰু ব্যাসেই বৃত্তৰ বৃহত্তম জ্যা।

"পাই" (π) হল বৃত্তৰ পৰিধি আৰু ব্যাসৰ অনুপাত, যি এক ধ্ৰূবক। পাই অত্যন্ত বিখ্যাত এটি ধ্ৰূবক। গণিতবিদৰ মতে পাই হ’ল বিশ্বৰ সবাতোকৈ সুন্দৰ ধ্ৰুৱক।

বৃত্তৰ ভিতৰৰ চক্ৰ আকাৰৰ অঞ্চলটিৰ ক্ষেত্ৰফল ${\displaystyle \pi }$ আৰু তাৰ ব্যাসাৰ্ধৰ বৰ্গৰ গুণফলৰ সমান।

${\displaystyle Area=\pi \cdot r^{2}$

বৃত্তৰ কেন্দ্ৰৰ পৰা ইয়াৰ পৰিসীমালৈ বা পৰিধিলৈ টনা ৰেখাখণ্ডকে ব্যাসাৰ্ধ বোলে। ব্যাসৰ অৰ্ধ, অৰ্থাৎ এটা বৃত্তৰ ব্যাসৰ মানৰ আধায়েই ব্যাসাৰ্ধ।

ব্যাসাৰ্ধ(r)= ১/২ × ব্যাস(d)^[2]

কোনো বৃত্তৰ 'কালি'(A)ৰ পৰা ব্যাসাৰ্ধ(r) নিৰ্ণয়ৰ বাবে

${\displaystyle r={\sqrt {\frac {A}{\pi }.}$

সূত্ৰ ব্যৱহাৰ কৰিব পাৰোঁ।

1. Chronology for 30000 BC to 500 BC
2. Squaring the circle
3. Measurement of a Circle by Archimedes
4. Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007.
5. Harkness, James (1898). Introduction to the theory of analytic functions. London, New York: Macmillan and Co.. pp. 30.
6. Ogilvy, C. Stanley, Excursions in Geometry, Dover, 1969, 14–17.
7. Altshiller-Court, Nathan, College Geometry, Dover, 2007 (orig. 1952).