Düz xətt

Düz xətt — həndəsənin əsas elementlərindən biridir. Həndəsənin sistematik təsviri zamanı düz xətt yalnız birbaşa olmayan şəkildə aksiomalarla təsbit edilir.
Düz xəttin aşağıdakı xassələri vardır:
- İki üst-üstə düşməyən nöqtədən yalnız bir düz xətt keçirmək olar.
- Müstəvi üzərində üst-üstə düşməyən iki düz xətt ya bir nöqtədə kəsişir, ya da paraleldir.
Üçölçülü fəzada iki düz xəttin qarşılıqlı vəziyyətini təsvir etmək üçün 4 variant mövcuddur:
- düz xətlər paraleldirlər;
- düz xətlər kəsişirlər;
- düz xətlər perpendikulyardırlar;
- düz xətlər çarpazdır;
Dekart koordinat sistemində düz xətti birdərcəli tənliklə ifadə etmək olur.
Kəsişən düz xətlər
Müstəvi üzərində iki müxtəlif düz xəttin bir ortaq nöqtəsi olarsa, onda deyirlər ki, bu düz xətlər kəsişir.
Paralel düz xətlər
Bir müstəvi üzərində üst-üstə düşməyən və kəsişməyən düz xətlər paralel düz xətlər adlanır.
Çarpaz düz xətlər
Fəzada paralel olmayan və kəsişməyən iki düz xətt çarpaz düz xətlər adlanır.
Düz xətt tənlikləri
Düz xəttin bucaq əmsalı tənliyi

OX oxuna perpendikulyar olmayan hər hansı düz xəttin verilməsini fərz edək. Bu düz xəttin absis oxu ilə əmələ gətirdiyi bucaq φ, ordinat oxundan ayırdığı parça olsun. Düz xətt üzərində şəkildəki kimi ixtiyari M(x,y) nöqtəsi götürək. Bu zaman,
Burada olduğunu nəzərə alsaq olar. Sonuncu tənliyə düz xəttin bucaq əmsalı tənliyi deyilir. olduqda olur və beləliklə də olur. Bu halda düz xətt absis oxuna paralel olur və düz xətt tənliyi şəklində olur. Bu isə ordinat oxundan b uzunluqda parça ayırıb, absis oxuna paralel olan düz xəttin tənliyidir.
Əgər düz xətt absis oxuna perpendikulyar olarsa, onda olur, bu halda isə olacaq, yəni k-nın bu qiyməti təyin edilməmişdir. Bu halda düz xəttin bütün nöqtələrinin basisləri eynidir və düz xəttin tənliyi şəklində olur. Beləliklə, bütün hallarda düz xətt x və y-lərə nəzərən birdərəcəli tənliklə xarakterizə olunur.
Düz xəttin ümumi tənliyi
XOY sistemində bir düz xətti təyin edən ümumi tənlik aşağıdakı kimidir:
Burada müxtəlif hallar mümkündür. Aşağıdakı cədvəl bu halları əhatə edir.[1]
| Əmsalların qiymətləri | Düz xəttin tənliyi | Düz xəttin vəziyyəti | |
|---|---|---|---|
| 1 | , , | İxtiyari düz xətt | |
| 2 | Düz xətt koordinat başlanğıcından keçir | ||
| 3 | , | OX oxuna paralele düz xətt | |
| 4 | OY oxuna paralel düz xətt | ||
| 5 | OX oxu üzərinə düşən düz xətt | ||
| 6 | OY oxu üzərinə düşən düz xətt |
Düz xəttin parçalarla tənliyi
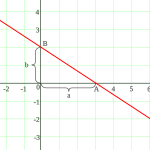
Şəkildə göstərildiyi kimi düz xətt koordinat oxlardan uyğun olaraq parçalarını kəsib keçir. Onda A, B olar. Bu nöqtələri nəzərə alaraq Düz xəttin parçalarla tənliyi aşağıdakı kimi verilir:
Belə halda xəttinə paralel olan düz xətt almaq mümkün olmur.
Həmçinin bax
İstinadlar
- ↑ Səlimov, Fazil; Zülfüqarov, Eldar. Ali Riyaziyyat I. Bakı: Çaşıoğlu. 2001. səh. 32-33. (#accessdate_missing_url)





























