Кайрско петоъгълно пано

Кайрското петоъгълно пано е пано от Евклидова плоскост. Името идва от факта, че няколко от улиците в Кайро са павирани по този начин.[1][2] Използваните петоъгълници са симетрични, но с една по-къса страна. То е едно от 15-те познати моноедрични петоъгълни пана. Неговото дуално е скосеното квадратно пано.
Нарича се също пано на МакМахон по името на Пърси Александър МакМахон след негова публикация New Mathematical Pastimes от 1921 г.[3][4] Конуей нарича паното четирикратен пентил.[5]

Петоъгълниците, с които се реализира покритието, не са правилни: една от страните е по-къса (sqrt(3)-1) и два от ъглите са прави (90°), докато останалите са тъпи (120°), но фигурата е симетрична. Четири петоъгълника образуват сплеснат шестоъгълник, фигура с която лесно се намира решението за плътно покритие.
Варианти
За кайроското пано са известни варианти, използващи плочки с по-ниска симетрия. Например, петоъгълникът може да има две различни двойки равни страни и два прави ъгъла.
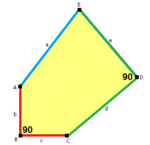
B=D=90°

Дуално пано
Каирското пано е дуално на покритие, получено от подреждане на два квадрата и три равностранни триъгълника около всеки връх:[6] правите ъгли на всяка от плочките задават центровете на квадратите, а тъпите ъгли - тези на триъгълниците.
Дуални четиричетириъгълни пана
- квадратно пано
- четириделно квадратно пано
- квадратно пано
- четириделно квадратно пано
- квадратно пано
- квадратно пано
- четириделно квадратно пано
- кайрско петоъгълно пано и призматично петоъгълно пано
Четириредови цветни петоъгълни пана
- квадратен трапецоедър
- петоъгълен икоситетраедър
- кайрско петоъгълно пано
- четирипеторедово цветно петоъгълно пано
- четиришесторедово цветно петоъгълно пано
- четириседморедово цветно петоъгълно пано
- четириосморедово цветно петоъгълно пано
- четиридеветоредово цветно петоъгълно пано
Източници
- ↑ Alsina, Claudi, Nelsen, Roger B. Charming proofs: a journey into elegant mathematics. Т. 42. Mathematical Association of America, 2010. ISBN 978-0-88385-348-1. p. 164. (на английски).
- ↑ Martin, George Edward. Transformation Geometry: An Introduction to Symmetry. Springer, 1982. ISBN 978-0-387-90636-2. с. 119.
- ↑ O'Keeffe, M., Hyde, B. G. Plane nets in crystal chemistry. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. Т. 295. 1980. с. 553–618.
- ↑ Macmahon, Major P. A. New Mathematical Pastimes. University Press, 1921.
- ↑ 4-fold pentille, използвайки неологизми със суфикс -tille, което да смесва „решетка“ (grille) и „плочка“ (tile), вж. Conway J., et al., The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1] Архив на оригинала от 2010-09-19 в Wayback Machine., p.288 (table)
- ↑ Шаблон:MathWorld
| Тази страница частично или изцяло представлява превод на страницата Cairo pentagonal tiling в Уикипедия на английски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |
