Квадратно уравнение
Квадратно уравнение в математиката се нарича уравнение от втора степен от вида
- ,
където е неизвестното, а коефициентите и са реални или комплексни числа и .
Ако и или и , уравнението е непълно квадратно,
а при и то става линейно.
Лявата страна на квадратното уравнение
е многочлен (полином) от втора степен и се нарича квадратен тричлен.
Корен на квадратното уравнение е всяка стойност на неизвестното , за която се изпълнява равенството. Тази стойност се нарича още корен на квадратния тричлен .
Елементите на квадратното уравнение имат свои имена:[1]
- се нарича първи или водещ коефициент,
- се нарича втори, среден коефициент или коефициент на ,
- се нарича свободен член.
Нормирано уравнение или приведено в нормиран вид е квадратно уравнение, в което водещият коефициент е равен на единица .[1] Привеждането се извършва чрез разделяне на цялото уравнение на водещия коефициент :
- .
Решаване на квадратни уравнения
Решаването на квадратното уравнение, както на всяко уравнение, се заключава в изчисляване на неговите корени. Това може да стане по различни методи и начини за различни случаи.
I метод. Обща формула за изчисляване на корени с дискриминанта
Пълното квадратно уравнение се решава по следния начин:
Умножава се всяка част на и се прибавя :
- .
Дискриминанта на квадратното уравнение се нарича величината .
- За случая
- (1)
- Формулата за случая е частен случай на формула (1):
- За случая квадратният корен от отрицателно число не е реално число. Уравнението няма реални корени и решението се получава от формула (1) във вид на два комплексни корена:
- . (2)
| Условие | |||
|---|---|---|---|
| Брой корени | Два различни реални корена |
Един двоен корен (два равни корена) |
Няма реални корени – 2 комплексни корена |
| Формула | (1) | (2) |
Следствия:
- тричленът е идеален квадрат на сума или разлика тогава и само тогава, когато ;
- Дискриминантата може да се намери с формулата: ;
- .
Този метод е универсален, но не единствен.
II метод. Съкратена формула при четен коефициент b
За уравнения от вида
- ,
където , тоест за четно , вместо формула (1) за намиране на корените е възможно да се използват по-прости изрази.[1]
Забележка: Формулите по-долу за ненормирано и нормирано квадратно уравнение могат да бъдат получени след заместване на израза в стандартните формули чрез прости преобразования. По-удобно е да се изчисли стойността на четвърт дискриминанта , при което всички необходими свойства са запазени.
| Дискриминанта | Корени | |||
|---|---|---|---|---|
| ненормирано | нормирано | D > 0 | ненормирано | нормирано |
| ; | . | . | ||
| D = 0 | ||||
III метод. Решаване на непълни квадратни уравнения
Използва се специален подход за решаване на „непълни“ квадратни уравнения. Разглеждат се три възможни ситуации.
| b = 0; c = 0 | b = 0; c ≠ 0 | b ≠ 0; c = 0 |
|---|---|---|
|
Ако , тогава уравнението има два реални корена (различни по знак) и ако , тогава уравнението няма реални корени. |
или Такова уравнение „непременно има два реални корена“, като единият от тях винаги е равен на нула. |
IV метод. Използване на частни съотношения на коефициенти
Има специални случаи на квадратни уравнения, в които коефициентите са във връзка един с друг, което ги прави много по-лесни за решаване.
Корени на квадратно уравнение, в което сборът от водещия коефициент и свободния член е равен на втория коефициент
Ако в квадратно уравнение сборът от първия коефициент и свободния член е равен на втория коефициент , тогава корените на уравнението са и числото, противоположно на отношението на свободния член към водещия коефициент .
От това следва, че преди решаването на всяко квадратно уравнение е препоръчително да се провери възможността за прилагане на тази теорема към него: сравнява се сумата от водещия коефициент и свободния член с втория коефициент.
Корени на квадратно уравнение, чиято сума от всички коефициенти е нула
Ако в едно квадратно уравнение сумата от всички коефициенти е равна на нула , тогава неговите корени са и съотношението на свободния член към водещия коефициент .
От това следва, че преди да се реши уравнение с помощта на стандартни методи, е препоръчително да се провери приложимостта на тази теорема към него, а именно дали сумата от всичките му коефициенти не е равна на нула.
| Съотношение на коефициентите | ||
V метод. Разлагане на квадратния тричлен на линейни множители
Ако квадратният тричлен : има неотрицателна дискриминанта, той се разлага на линейни множители по следния начин:
където са корените на уравнението .
Ако дискриминантата на квадратния тричлен е отрицателна, той не може да се разложи на линейни множители с реални коефициенти. В този случай казваме, че квадратният тричлен е неразложим.
Членът е множител на квадратния тричлен
тогава и само тогава, когато е корен на квадратното уравнение
Това следва от формулата за разлагане на квадратно уравнение на множители
или при
В специалния случай, когато квадратното уравнение има един двоен корен, т.е. дискриминантата е нула, квадратният тричлен може да се разложи на множителите:
Така чрез разлагане на квадратния тричлен на линейни множители решаването на квадратното уравнение се свежда до решаването на линейни уравнения.
VI метод. Допълване до точен квадрат на нормирано уравнение
Уравнението
се решава чрез допълване до точен квадрат. Това е често прилаган в практиката метод, както при пълното квадратно уравнение (I метод):
Ако в реалния случай тук се получи под корена отрицателно число, последните две стъпки естествено не са допустими. В този случай на третия ред се вижда, че не може да има реално решение, защото дясната страна е отрицателна, а лявата като квадрат не е отрицателна.
Методът може да се разглежда като частен случай на разлагане на квадратния тричлен на еднакви линейни множители.
VII метод. Формули на Виет
Полезни връзки между корените и коефициентите на квадратното уравнение са установени от френския математик Франсоа Виет през XVII в. и поради това носят неговото име.
Права теорема на Виет: Ако и са корените на квадратното уравнение
- , то
- ,
Обратна теорема на Виет: Ако числата и са такива, че и , то тези числа са корени на уравнението .
VIII метод. Преобразуване със заместване
По своята същност този метод е просто модификация на теоремата на Виет.
Методът „Преобразуване със заместване“ е привеждане на уравнение, което не може да се преобразува така, че всичките му коефициенти да останат цели, към нормирано квадратно уравнение с цели коефициенти чрез смяна на променливата:
1) Умножават се двете части на уравнението по водещия коефициент :
2) Замества се
Решава се полученото уравнение спрямо по описания метод за нормирано уравнение и после се намира .
Графично решение на квадратно уравнение
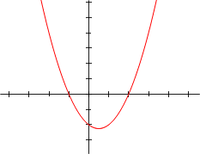
на реалната променлива , абсцисите на точките, в които графиката пресича оста , а именно и , са корени на квадратното уравнение .
Корените на квадратното уравнение
са и нули на квадратната функция
тъй като те са стойности на x, за които
Ако и са реални числа и дефиниционната област на е множеството на реалните числа, тогава нулите на са абсцисите на точките, в които графиката на функцията пресича оста . От горното следва, че ако дискриминантата е положителна, графиката пресича оста в две точки; ако тя е нула, графиката се допира до оста в една точка и ако е отрицателна, графиката не пресича оста .
Уравнения, които се свеждат към квадратни
Алгебрични
Уравнения от висока степен като
могат да се сведат до квадратни уравнения
- ,
където
- .
Забележително е, че най-високата степен е равна на удвоената степен на средния член. Полученото квадратно уравнение може да се реши директно или с проста субституция, като се използват методите за решаване на квадратни уравнения като разлагане на множители, допълване до точен квадрат и др.
Най-общо, ако полиномът е квадратен тричлен относно някоя променлива , където
- ,
тогава квадратното уравнение може да помогне, за да се реши уравнението от високата степен.
Методът е особено популярен при решаване на биквадратно уравнение (уравнение с едно неизвестно на четвърта и втора степен: и ).
Диференциални
Вижте също
- Квадратна функция
- Линейно уравнение
- Кубично уравнение
- Биквадратно уравнение










































































































