1 + 1 + 1 + 1 + ⋯
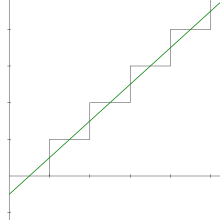
En matemàtiques, 1 + 1 + 1 + 1 + ⋯, també escrit , , o senzillament , és una sèrie divergent, és a dir: la seva seqüència de sumes parcials no convergeix a un límit en els nombres reals. Es pot entendre la seqüència 1n com a sèrie geomètrica amb la proporció comuna 1. A diferència d'altres sèries geomètriques amb ratio racional (excepte −1), convergeix dins ni els números reals ni en el pp-adic números per algun p. En el context de la recta real estesa
ja que la seva seqüència de sumes parcials creix monòtonament sense estar fitada per dalt.
Sempre que la suma de n0 aparegui en aplicacions físiques, es pot interpretar de vegades com la regularització de la funció zeta, com el valor per s = 0 de la funció zeta de Riemann:
Tanmateix, les dues fórmules que s'han donat no són vàlides per zero, però la continuació analítica és
Utilitzant aquesta s'obté (atès que Γ(1) = 1),
on la l'expansió en sèrie de potències de ζ(s) al voltant de s = 1 segueix ja que ζ(s) hi té un pol simple de residu. En aquest sentit 1 + 1 + 1 + 1 + ⋯ = ζ(0) = −12 .
Emilio Elizalde va comentar sobre aquesta sèrie:
| « | En un breu període de menys d'un any, dos físics distingits, A. Slavnov i F. Yndurain, van donar seminaris a Barcelona, sobre diferents temes. Va ser sorprenent que, en totes dues presentacions, en alguns moment el ponent s'adrecés al públic i digués les següents paraules: 'Com tothom sap, 1 + 1 + 1 + ⋯ = −12.' Potser volien dir: Si no saps això, no et servirà de res seguir escoltant.[2] | » |
Vegeu també
Referències
- ↑ Tao, Terence (April 10, 2010), The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation, <http://terrytao.wordpress.com/2010/04/10/the-euler-maclaurin-formula-bernoulli-numbers-the-zeta-function-and-real-variable-analytic-continuation/>. Consulta: 30 gener 2014
- ↑ Elizalde, Emilio. «Proceedings of the II International Conference on Fundamental Interactions». A: , 2004.
Enllaços externs
- Seqüència A000012 OEIS: La seqüència de nombres positius més simple: la seqüència de només 1s








