Lògica temporal
La lògica temporal és un tipus de lògica modal usada per a descriure un sistema de regles i simbolismes per a la representació i el raonament sobre proposicions en les quals té presència el factor temps. Hi ha una certa relació amb altres varietats de lògica, per exemple, la lògica modal. El seu estudi té una certa importància dins l'estudi de la informàtica, en particular els desenvolupaments introduïts per Amir Pnueli.
Per exemple, prenguem la sentència: "Tinc gana"; encara que el seu significat és independent del temps, el seu valor de veritat o falsedat pot variar amb el temps en un determinat sistema que inclogui accions de menjar; així, en funció del sistema, algunes vegades serà certa i d'altres falsa, encara que mai serà certa i falsa simultàniament.
Història
La lògica temporal va ser estudiada per primera vegada per Aristòtil; en alguns dels seus escrits, apareixen expressions que guarden una semblança amb una lògica temporal de primer ordre; així, apareixen expressions amb quantificadors existencials i quantificadors universals, al costat de seqüències d'estats d'un ordre temporal que, en la pràctica és una lògica temporal.
Sistemes basats en lògica temporal
En lògica temporal, apareixen els mateixos operadors que en una lògica de primer ordre, juntament amb d'altres de nous, entre els quals es poden trobar: sempre, algunes vegades i mai.
Alguns sistemes lògics basats en lògica temporal són: lògica computacional en arbre (computational tree logic, CTL), lògica temporal lineal (Linear temporal logic, LTL), lògica temporal d'intervals (interval temporal logic, ITL) i lògica d'accions temporal (temporal logic of actions, TLA).
Operadors temporals
La lògica temporal té dues classes d'operadors: operadors lògics i operadors modals (Stanford). Els operadors lògics són normalment operadors de funcions de veritat (truth-functional: ). Els operadors modals fan servir la lògica linear temporal (linear temporal logic) i la lògica computacional en arbre (computation tree logic) i són definits com segueix:
| Textual | Símbòlic | Definició | Explicació | Diagrama |
| Operadors binaris | ||||
| U | Fins: s'acompleix en l'estat actual o un de posterior, i s'ha d'acomplir fins a aquesta posició, a partir de la qual, no cal que continuï acomplint-se. |  | ||
| R | Alliberament: alliberaments si s'acompleix fins que la primera posició en què s'acompleix (o sempre si aquesta posició no existeix). |  | ||
| Operadors unaris | ||||
| X | Següent: s'acompleix en l'estat següent (X s'usa com a sinònim). |  | ||
| F | Finalment: eventualment s'acompleix (en algun lloc del camí). |  | ||
| G | Global: s'ha d'acomplir en tot el camí. |  | ||
| A | Tots: s'ha d'acomplir en tots els camins començant en l'estat actual. | |||
| E | Existeix: existeix com a mínim un camí que surt en l'estat actual en què s'acompleix. | |||
Símbols alternatius:
- L'operador R,de vegades denotat per V
- L'operador W és l'operador feble fins (weak until): és equivalent a
Operadors unaris són fórmules ben formades (well-formed formula) sempre que B () és ben format. Els operadors binaris són fórmules ben formades sempre que B () i C () són ben formades.
En algunes lògiques, alguns operadors no poden ser expressats. Per exemple, l'operador N no pot ser expressat en la lògica d'accions temporal (temporal logic of actions).
Equivalències
- en què V = vertader
Exemple
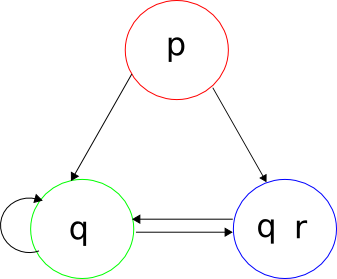 A la figura, es mostra una estructura de Kripke de tres estats. Es pot descriure de la manera següent:
A la figura, es mostra una estructura de Kripke de tres estats. Es pot descriure de la manera següent:
- A l'estat vermell (iR) es compleix p, i hi ha transicions cap a la resta dels estats.
- A l'estat verd (iV) qés veritable, i les transicions van cap a l'estat blau o el mateix estat.
- A l'estat blau (iA) són veritables q i r, i té una única transició, cap a l'estat verd.
Si es considera arbitràriament l'estat vermell com a estat inicial, es compleix el següent:
- EX r: puix prenent el camí iR iA i V i V ..., en el segon estat (iA) r és vertader, amb el qual es troba un camí que compleix X r.
- AF q: puix per qualsevol camí que s'esculli, inevitablement caldrà entrar en els estats que fan complir q, és a dir, iV ae A.
Referències
- Venema, Yde, 2001, "Temporal Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- E. A. Emerson and C. Lei, modalities for model checking: branching time logic strikes back, in Science of Computer Programming 8, p 275-306, 1987.
- E. A. Emerson, temporal and modal logic, Handbook of Theoretical Computer Science, Chapter 16, the MIT Press, 1990.





















