Marge d'error
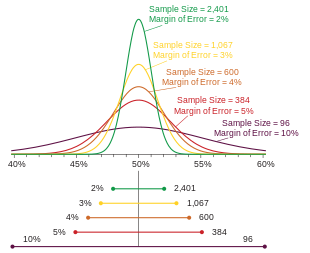
El marge d'error, en estadística, és una estimació de la mesura que poden tenir els resultats d'una enquesta si es repeteix l'enquesta. Com més gran sigui el marge d'error, menys fiables seran els resultats i major serà la probabilitat que es desvien de la realitat.[1]
El marge d’error es pot calcular directament a partir de la mida de la mostra (per exemple, el nombre d’enquestats) i sol ser informat per un dels tres nivells diferents de l'interval de confiança.[2][3] El nivell del 99 % és el més conservador, el nivell del 95% és el més comú i el nivell de 90% s'utilitza poques vegades. Per obtenir un nivell de confiança de 99 %, estem segurs al 99% que el valor real es troba dins del marge d'error del valor enquestat.
El marge d'error només té en compte l'error de la mostra. No té en compte altres fonts potencials d'error, en particular, el biaix en les preguntes o l'exclusió que un grup no sigui qüestionat, el fet que algunes persones no vulguin respondre, el fet que algunes persones menteixin, o els errors de càlcul.
Comprensió
Exemple
Per il·lustrar els conceptes explicats a l'article, farem servir l'exemple de la campanya presidencial dels EUA del 2004. Segons una enquesta a Newsweek, el 47 % dels votants votaria per John Kerry si les eleccions tinguessin lloc avui.[4] El 45% votaria per George W. Bush i el 2% per a Ralph Nader. La mida de la mostra és de 1.013 enquestats i el marge d’error és de ± 4 ppc. A la resta de l'article farem servir l'interval de confiança del 99 %.[5]
Concepte bàsic
Una enquesta requereix prendre una mostra de la població. En el cas del Newsweek, la població considerada és la gent que votarà. Davant la impossibilitat d’interrogar tots els votants, els instituts electorals construeixen mostres que normalment són representatives de la població. És possible que qüestionin 1.013 persones que votaran per Bush quan en realitat els votants estiguin dividits, però això és molt poc probable si la mostra és prou representativa de la població.
Termes i càlculs estadístics
Aquesta secció tracta breument l'error estàndard d'un resultat, l'interval de confiança, i relaciona aquests dos conceptes amb el marge d'error. Per simplificar, els càlculs suposen que l'enquesta es basa en una mostra aleatòria simple d'una gran població.
L'error estàndard d'una proporció o percentatge p és el seu nivell de precisió i representa la desviació estàndard d'aquest percentatge. Es pot estimar utilitzant p i la mida de la mostra n, sempre que n sigui inferior al 5% de la mida de la població N. En el cas de l'enquesta encarregada per Newsweek, el percentatge de vots de Kerry p = 0,47 i n = 1.013.[6]
Per obtenir el marge d'error, simplement multipliquem l'error estàndard per obtingut a partir del llindar de confiança. En funció del llindar de confiança que vulguem fer servir, buscarem una determinada porció de l'àrea sota la corba normal (0,90, 0,95 o 0,99) que, per tant, estarà delimitada per , que representa el nombre de desviacions estàndard de les quals ens allunyarem al voltant de zero.
- Per obtenir un nivell de confiança del 95%,
- Per obtenir un nivell de confiança del 99%,
- Tinguis en compte que per obtenir un marge d'error en %, s'ha de multiplicar per 100:
L'interval de confiança de la proporció es defineix restant i afegint el marge d'error a la proporció: . O de nou, amb el percentatge: Això representa els límits inferior i superior en què trobarem la proporció real a la població. Normalment presentem un interval de confiança juntament amb el llindar de confiança que hem decidit utilitzar. Per exemple, per a un nivell de confiança del 95%, direm: 19 vegades sobre 20 (per tant, el 19 mostres de 20 realitzades sobre la mateixa població), el percentatge serà entre i .
Marge màxim d'error
Per a un mostreig aleatori simple d'una població molt gran, el marge màxim d'error es converteix en una simple reformulació de la mida de la mostra n. Els numeradors de les equacions següents s’arrodoneixen al segon decimal.
- Marge d'error al 99 %
- Marge d'error al 95 %
- Marge d'error a 90 %
L'explicació matemàtica és que per obtenir un marge d’error màxim, fem servir el valor màxim de de 0,50. Així arribem a:
El marge d'error no està completament definit si no s'informa l'interval de confiança. Si un article sobre una enquesta no proporciona l'interval de confiança, es pot aproximar el marge d'error per al nivell de confiança desitjat mitjançant la mida de la mostra mitjançant les fórmules indicades anteriorment. A més, si el marge d’error és del 95%, és possible calcular el marge d'error al 99% augmentant-lo en un 30%.
Efecte de la mida de la població
La fórmula que s’acaba de presentar per al marge d’error suposa una població infinitament gran i, per tant, no depèn de la mida de la població d’interès. Segons la teoria del mostreig, aquesta suposició és raonable quan la fracció de mostreig és petita. El marge d’error d’una mostra concreta és essencialment el mateix, independentment de si la població d’interès té la mida d’una escola, ciutat, província o país, sempre que la fracció de mostreig sigui inferior al 5% (en altres paraules, quan la població és inferior a 20 vegades la mostra).
- Per tant, la fórmula completa esdevé :
Per ajustar el marge d'error per a una fracció de mostreig gran, el factor de correcció el redueix. La fórmula sosté que com més s'acosta la mida de la mostra n a la mida de la població N, més proper s'apropa a zero el factor de correcció, la qual cosa té l'efecte de reduir la mida del marge d'error. Això té sentit intuïtiu ja que una mostra de la mida de la població (n = N) es converteix en un cens, on el marge d'error sol perdre la seva utilitat.
Comparació de percentatges
Càlculs
Per determinar si dos percentatges són significativament diferents entre si, simplement es podria comprovar si hi ha una superposició entre ells. Per fer-ho, només cal afegir-hi el marge d'error del percentatge més petit i restar a aquest últim el del més gran. Només queda comprovar si els valors es superposen. Si hi ha una superposició, direm que els dos percentatges no són significativament diferents, i viceversa.
D'altra banda, també hi ha una manera de calcular la diferència mínima necessària entre els dos percentatges perquè siguin significativament diferents per obtenir un resultat una mica menys conservador.
Per a dues proporcions que provenen de la mateixa mostra, farem servir el càlcul següent :
- o representa la primera proporció, el segon, i grandària de la mostra.
Per a dues proporcions que provenen de dues mostres diferents, per exemple de dues sondes, es fa el càlcul :
- o bé és la primera proporció, el segon, la mida de la primera mostra i la mida de la segona mostra.
Aquesta fórmula, però, s’acosta matemàticament a aquesta versió simplificada. :
- o bé representa la mitjana entre i , i la mitjana entre i .
representa la diferència mínima que cal trobar entre i de manera que es pot considerar significatiu. Per aconseguir-ho %, només cal realitzar .
Taules
El marge d’error s’utilitza freqüentment per determinar si un percentatge és superior a un altre. L'estadística que s'hauria d'utilitzar en aquest cas és simplement la probabilitat que un percentatge sigui superior a un altre. A la taula següent es mostra el " probabilitat de liderar »De dos candidats, en absència d'altres candidats, i assolint un nivell de 95 % de confiança:
| Diferència en percentatges : | 0 % | 1 % | 2 % | 3 % | 4 % | 5 % | 6 % | 7 % | 8 % | 9 % | 10 % |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 % marge d'error | 50,0 | 83,6 | 97,5 | 99,8 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2 % marge d'error | 50,0 | 68,8 | 83,7 | 92,9 | 97,5 | 99,3 | 99,8 | 100 | 100 | 100 | 100 |
| 3 % marge d'error | 50,0 | 62,8 | 74.3 | 83,7 | 90,5 | 94,9 | 97,5 | 98,9 | 99,6 | 99,8 | 99,9 |
| 4 % marge d'error | 50,0 | 59,7 | 68,8 | 76,9 | 83,7 | 89,0 | 93,0 | 95,7 | 97,5 | 98,7 | 99,3 |
| 5 % marge d'error | 50,0 | 57,8 | 65.2 | 72.2 | 78,4 | 83,7 | 88.1 | 91,5 | 94,2 | 96.2 | 97,6 |
| 6 % marge d'error | 50,0 | 56,5 | 62,8 | 68,8 | 74.3 | 79,3 | 83,7 | 87,4 | 90,5 | 93,0 | 95,0 |
| 7 % marge d'error | 50,0 | 55,6 | 61,0 | 66.3 | 71.2 | 75,8 | 80,0 | 83,7 | 86,9 | 89,7 | 92,0 |
| 8 % marge d'error | 50,0 | 54,9 | 59,7 | 64.3 | 68,8 | 73,0 | 76,9 | 80,5 | 83,7 | 86,6 | 89.1 |
| 9 % marge d'error | 50,0 | 54.3 | 58,6 | 62,8 | 66,9 | 70,7 | 74.4 | 77,8 | 80,9 | 83,7 | 86,3 |
| 10 % marge d'error | 50,0 | 53,9 | 57,8 | 61,6 | 65.3 | 68,8 | 72.2 | 75,4 | 78,4 | 81.2 | 83,8 |
Per exemple, les probabilitats que John Kerry guanyi George Bush segons les dades de l'enquesta de Newsweek % i un marge d'error de 3 %) és aproximadament del 74,3 %, sempre que utilitzessin un nivell de 95 % de confiança. Aquí teniu la mateixa taula per a un nivell de 99 % de confiança:
| Diferència en percentatges : | 0 % | 1 % | 2 % | 3 % | 4 % | 5 % | 6 % | 7 % | 8 % | 9 % | 10 % |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 % marge d'error | 50,0 | 90,1 | 99,5 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2 % marge d'error | 50,0 | 74.1 | 90,2 | 97,4 | 99,5 | 99,9 | 100 | 100 | 100 | 100 | 100 |
| 3 % marge d'error | 50,0 | 66,6 | 80,5 | 90,2 | 95,7 | 98,4 | 99,5 | 99,9 | 100 | 100 | 100 |
| 4 % marge d'error | 50,0 | 62,6 | 74.1 | 83,3 | 90,2 | 94,7 | 97,4 | 98,8 | 99,5 | 99,8 | 99,9 |
| 5 % marge d'error | 50,0 | 60.2 | 69,7 | 78,1 | 84,9 | 90,2 | 94,0 | 96,5 | 98,1 | 99,0 | 99,5 |
| 6 % marge d'error | 50,0 | 58,5 | 66,6 | 74.1 | 80,5 | 85,9 | 90,2 | 93,4 | 95,8 | 97,4 | 98,5 |
| 7 % marge d'error | 50,0 | 57.3 | 64,4 | 71,0 | 77,0 | 82,2 | 86,6 | 90,2 | 93,0 | 95,2 | 96,8 |
| 8 % marge d'error | 50,0 | 56,4 | 62,6 | 68,6 | 74.1 | 79,0 | 83,4 | 87,1 | 90,2 | 92,7 | 94,7 |
| 9 % marge d'error | 50,0 | 55,7 | 61.3 | 66,6 | 71,7 | 76,3 | 80,6 | 84,3 | 87,5 | 90,2 | 92,5 |
| 10 % marge d'error | 50,0 | 55.1 | 60.2 | 65.1 | 69,7 | 74.1 | 78,1 | 81,7 | 85,0 | 87,8 | 90,3 |
Si l'enquesta de Newsweek utilitza un nivell de 99 % de confiança, llavors les probabilitats de guanyar Kerry a Bush serien de 74,1 %. (El marge d'error augmenta fins al 4%). Per tant, sembla obvi que el nivell de confiança té un impacte significatiu en la probabilitat de guanyar.
Càlculs avançats
Sigui N el nombre de votants de la mostra. Suposem que es van dibuixar de manera aleatòria i independent de la població total. La hipòtesi és potser massa forta, però si la constitució de la mostra es fa amb cura, la realitat almenys pot abordar aquesta situació. Sigui p la proporció d'electors de la població total que votarà " Sí ". A continuació, el nombre X de votants de la mostra que votaran " Sí »És una variable aleatòria distribuïda segons una distribució binomial dels paràmetres N i p. Si N és prou gran, llavors X segueix la distribució normal de la mitjana Np i la variància Np (1 - p).[2][7] Tan
segueix la llei normal centrada reduïda (la que té els paràmetres 0 i 1).
La taula de la distribució normal revela que P (-2,576 < Z <2,576) = 0,99, o, dit d’una altra manera, que hi ha 99 de cada cent possibilitats que es produeixi aquest esdeveniment. D'aquesta manera,
Això equival a
La substitució de p en el primer i el tercer membres d'aquesta desigualtat pel valor estimat X / N rarament resulta en grans errors si N és prou gran. Aquesta operació té com a resultat:
El primer i el tercer membres de la desigualtat depenen del valor observable X / N i del valor no observable p, i són els valors extrems de l’interval de confiança. En altres paraules, el marge d'error és
Cas de sistemes vius i complexos
En sistemes complexos, especialment en el camp de la biologia i encara més en l'ecologia o el clima, en el camp de les dosis baixes, etc., els marges d’error poden ser grans, sobretot a causa dels freqüents efectes ocults. No es tenen en compte a causa de la dificultat per separar els aspectes biòtics i abiòtics de certes circumstàncies reals (in situ) o experimentals al laboratori, in vitro, en un espai reduït.[8] o certs efectes estocàstics .
Referències
- ↑ Wonnacott, T.H. and R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.
- ↑ 2,0 2,1 Lohr, Sharon L. Sampling : design and analysis. Pacific Grove, CA: Duxbury Press, 1999. ISBN 0-534-35361-4.
- ↑ Weisstein, Eric W. «Margin of Error» (en anglès). [Consulta: 3 novembre 2021].
- ↑ Fogo, José Carlos. «Técnicas de Amostragem». UFSCAR. Arxivat de l'original el 2017-03-29. [Consulta: 6 juny 2017].
- ↑ Fineman, Howard. «Ninety Minutes Later, A New Race» (en anglès), 10-10-2004. [Consulta: 3 novembre 2021].
- ↑ «USA TODAY Education - Democracy TODAY». [Consulta: 3 novembre 2021].
- ↑ «What is a Margin of Error?». [Consulta: 3 novembre 2021].
- ↑ Michael A. Huston, Hidden treatments in ecological experiments: re-evaluating the ecosystem function of biodiversity Arxivat 2010-06-30 a Wayback Machine. ; Oecologia (1997) 110:449±460 Ó Springer-Verlag 1997
Bibliografia
- Sudman, Seymour; Bradburn, Norman. Asking Questions: A Practical Guide to Questionnaire Design (en anglès). 1st. San Francisco: Jossey-Bass. ISBN 0-87589-546-8.
- Wonnacott, Thomas H. Introductory statistics (en anglès). 5th. New York: Wiley, 1990. ISBN 0-471-61518-8.
































