Procés irreversible

En ciència, un procés que no és reversible s'anomena irreversible. Aquest concepte sorgeix freqüentment en termodinàmica. Tots els processos naturals complexos són irreversibles, ^[1][2][3] encara que una transició de fase a la temperatura de coexistència (per exemple, la fusió de glaçons a l'aigua) és ben aproximada com a reversible.

En termodinàmica, un canvi en l'estat termodinàmic d'un sistema i de tot el seu entorn no es pot restaurar amb precisió al seu estat inicial mitjançant canvis infinitesimals en alguna propietat del sistema sense despesa d'energia. Un sistema que pateix un procés irreversible encara pot ser capaç de tornar al seu estat inicial. Com que l'entropia és una funció d'estat, el canvi d'entropia del sistema és el mateix tant si el procés és reversible com irreversible. No obstant això, la impossibilitat es produeix en restaurar l' entorn a les seves pròpies condicions inicials. Un procés irreversible augmenta l'entropia total del sistema i el seu entorn. La segona llei de la termodinàmica es pot utilitzar per determinar si un procés hipotètic és reversible o no.

Intuïtivament, un procés és reversible si no hi ha dissipació. Per exemple, l'expansió Joule és irreversible perquè inicialment el sistema no és uniforme. Inicialment, hi ha una part del sistema amb gas, i una part del sistema sense gas. Perquè es produeixi la dissipació, cal que hi hagi una falta d'uniformitat. Això és el mateix que si en un sistema una secció del gas fos calenta i l'altra freda. Aleshores es produiria la dissipació; la distribució de la temperatura es faria uniforme sense treballar, i això seria irreversible perquè no es podria afegir ni eliminar calor ni canviar el volum per tornar el sistema al seu estat inicial. Així, si el sistema és sempre uniforme, aleshores el procés és reversible, és a dir, podeu tornar el sistema al seu estat original afegint o eliminant calor, treballant al sistema o deixant que el sistema funcioni. Com a altre exemple, per aproximar l'expansió en un motor de combustió interna com a reversible, suposaríem que la temperatura i la pressió canvien uniformement al llarg del volum després de l'espurna. Òbviament, això no és cert i hi ha una flama davantera i, de vegades, fins i tot el motor pica. Una de les raons per les quals els motors dièsel són capaços d'aconseguir una major eficiència és que la combustió és molt més uniforme, de manera que es perd menys energia per dissipació i el procés és més proper al reversible.

El fenomen de la irreversibilitat deriva del fet que si un sistema termodinàmic, que és qualsevol sistema de complexitat suficient, de molècules que interactuen es porta d'un estat termodinàmic a un altre, la configuració o disposició dels àtoms i molècules del sistema canviarà d'una manera manera que no és fàcilment previsible.^[4][5] S'utilitzarà certa "energia de transformació" ja que les molècules del "cos de treball" treballen entre si quan canvien d'un estat a un altre. Durant aquesta transformació, hi haurà una certa pèrdua o dissipació d'energia tèrmica a causa de la fricció intermolecular i els xocs. Aquesta energia no serà recuperable si el procés s'inverteix.

S'ha trobat que molts processos biològics que abans es pensaven que eren reversibles són en realitat una parella de dos processos irreversibles. Mentre que es va creure que un únic enzim catalitzava tant els canvis químics directes com els inversos, la investigació ha descobert que normalment es necessiten dos enzims separats d'estructura similar per dur a terme el que resulta en un parell de processos termodinàmicament irreversibles.

La termodinàmica defineix el comportament estadístic d'un gran nombre d'entitats, el comportament exacte de les quals ve donat per lleis més específiques. Tot i que les lleis teòriques fonamentals de la física són totes reversibles en el temps, experimentalment la probabilitat de reversibilitat real és baixa i l'estat anterior del sistema i l'entorn només es recupera fins a cert punt (vegeu: principi d'incertesa). La reversibilitat de la termodinàmica ha de ser de naturalesa estadística; és a dir, ha de ser simplement altament improbable, però no impossible, que un sistema baixi en entropia. És a dir, la reversibilitat del temps es compleix si el procés passa de la mateixa manera si el temps passa a la inversa o s'inverteix l'ordre dels estats del procés (l'últim estat es converteix en el primer i viceversa).

El físic alemany Rudolf Clausius, a la dècada de 1850, va ser el primer a quantificar matemàticament el descobriment de la irreversibilitat a la natura mitjançant la seva introducció del concepte d'entropia. A les seves memòries de 1854 "Sobre una forma modificada del segon teorema fonamental en la teoria mecànica de la calor", Clausius afirma:

«Pot, a més, succeir que en lloc d'una transmissió de calor descendent que acompanyi, en un mateix procés, la transmissió ascendent, es produeixi un altre canvi permanent que tingui la particularitat de no ser reversible sense ser substituït per un nou permanent. canvi d'un tipus similar, o produint una transmissió descendent de calor. »

Simplement, Clausius afirma que és impossible que un sistema transfereixi calor d'un cos més fred a un cos més calent. Per exemple, una tassa de cafè calent col·locada en una zona a temperatura ambient (~72 °F) transferirà calor al seu entorn i, per tant, es refredarà amb la temperatura de l'habitació augmentant lleugerament (fins a ~72.3 °F ). No obstant això, aquesta mateixa tassa de cafè inicial mai absorbirà la calor del seu entorn, la qual cosa farà que s'escalfi encara més, amb la disminució de la temperatura de l'habitació (fins a ~71.7 °F ). Per tant, el procés de refredament del cafè és irreversible tret que s'afegeixi energia addicional al sistema.

Tanmateix, va sorgir una paradoxa quan es va intentar conciliar la microanàlisi d'un sistema amb les observacions del seu macroestat. Molts processos són matemàticament reversibles en el seu microestat quan s'analitzen mitjançant la mecànica newtoniana clàssica. Aquesta paradoxa contamina clarament les explicacions microscòpiques de la tendència macroscòpica cap a l'equilibri, com l'argument de James Clerk Maxwell de 1860 que les col·lisions moleculars comporten una igualació de temperatures de gasos barrejats.^[6] De 1872 a 1875, Ludwig Boltzmann va reforçar l'explicació estadística d'aquesta paradoxa en forma de fórmula d'entropia de Boltzmann, afirmant que un augment del nombre de possibles microestats en què podria estar un sistema augmentarà l'entropia del sistema, fent-lo menys probable. que el sistema tornarà a un estat anterior. Les seves fórmules van quantificar l'anàlisi feta per William Thomson, primer baró Kelvin, que havia argumentat que: ^[7][8]

«Les equacions de moviment en dinàmica abstracta són perfectament reversibles; qualsevol solució d'aquestes equacions roman vàlida quan la variable temporal t se substitueix per –t. D'altra banda, els processos físics són irreversibles: per exemple, la fricció dels sòlids, la conducció de la calor i la difusió. No obstant això, el principi de dissipació d'energia és compatible amb una teoria molecular en què cada partícula està subjecta a les lleis de la dinàmica abstracta. »

Una altra explicació dels sistemes irreversibles va ser presentada pel matemàtic francès Henri Poincaré. El 1890, va publicar la seva primera explicació de la dinàmica no lineal, també anomenada teoria del caos. Aplicant la teoria del caos a la segona llei de la termodinàmica, la paradoxa de la irreversibilitat es pot explicar en els errors associats a l'escala de microestats a macroestats i els graus de llibertat utilitzats en fer observacions experimentals. Sensibilitat a les condicions inicials relacionades amb el sistema i el seu entorn en els compostos microestatals en una exposició de característiques irreversibles dins de l'àmbit físic observable.

En l'àmbit físic, hi ha molts processos irreversibles als quals es pot atribuir la incapacitat d'aconseguir el 100% d'eficiència en la transferència d'energia. A continuació es mostra una llista d'esdeveniments espontanis que contribueixen a la irreversibilitat dels processos.

• Envelliment (aquesta afirmació es discuteix, ja que s'ha demostrat que l'envelliment s'inverteix en els ratolins.^[9] També s'ha demostrat que NAD+ ^[10] i la telomerasa ^[11] inverteixen l'envelliment).
• La mort
• Temps
• Transferència de calor mitjançant una diferència finita de temperatura
• Fricció
• Deformació plàstica
• Flux de corrent elèctric a través d'una resistència
• Magnetització o polarització amb una histèresi
• Expansió sense restriccions dels fluids
• Reaccions químiques espontànies
• Mescla espontània de matèria de composició/estats diferents

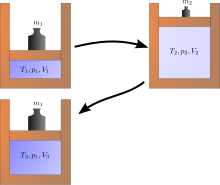
Una expansió de Joule és un exemple de termodinàmica clàssica, ja que és fàcil calcular l'augment resultant d'entropia. Es produeix quan un volum de gas es manté en un costat d'un recipient aïllat tèrmicament (a través d'una petita partició), amb l'altre costat del recipient s'evacua; llavors s'obre la partició entre les dues parts del recipient i el gas omple tot el recipient. L'energia interna del gas es manté igual, mentre que el volum augmenta. L'estat original no es pot recuperar simplement comprimint el gas fins al seu volum original, ja que l'energia interna augmentarà amb aquesta compressió. L'estat original només es pot recuperar refredant el sistema re-comprimit i, per tant, escalfant l'ambient de manera irreversible. El diagrama de la dreta només s'aplica si la primera expansió és "lliure" (expansió Joule), és a dir, no hi pot haver pressió atmosfèrica fora del cilindre i no hi ha pes aixecat.