Binární sčítačka
Binární sčítačka (nebo jen sčítačka) je kombinační logický obvod, který realizuje sčítání čísel reprezentovaných ve dvojkové soustavě. Je základní součástí aritmeticko-logických jednotek (ALU), ale také v dalších jednotkách, například pro práci s pamětí (MMU aj.), procesorů (CPU, GPU, DSP, ...) počítačů.
V případě použití dvojkového doplňku záporných čísel může být sčítačka velmi snadno rozšířena na sčítačku-odčítačku.
Jednobitové sčítačky
Poloviční sčítačka

Poloviční sčítačka nebo polosčítačka (anglicky Half adder) realizuje sčítání dvou jednobitových čísel. Vstup jsou dva jednobitové sčítance (A, B). Výstupem je jednobitový součet (S) a jednobitový příznak přenosu do vyššího řádu (C, nebo též anglicky jako Carry flag).
Poloviční sčítačka dále přenáší příznak přenosu do vyššího řádu, sama však nedokáže zpracovat přenos z nižšího řádu. Nestačí proto k realizaci vícebitového sčítání.
Pravdivostní tabulka poloviční sčítačky:
| vstup | výstup | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Úplná sčítačka



Úplná sčítačka (anglicky Full adder) realizuje sčítání dvou jednobitových čísel s přihlédnutím k přenosu z předchozího řádu. Vstupem jsou tři jednobitové sčítance: A, B, Ci (Ci z anglického Carry-in). Výstupem je jednobitový součet (S) a jednobitový příznak přenosu do vyššího řádu (Co z anglického Carry-out).
Úplnou sčítačku je možné složit ze dvou polovičních sčítaček a hradla OR (viz obrázek). Hradlo OR je navíc možné bez vlivu na funkčnost nahradit pomocí hradla XOR, protože kombinace vstupů (1, 1), v němž by se jejich výstupy lišily, nemůže v případě sčítání nastat (buď nastane přenos pouze v první poloviční sčítačce, nebo pouze v druhé). Takže k vytvoření úplné sčítačky stačí mít 2 typy hradel, což může být praktické pro realizaci.
Úplné sčítačky se spolu mohou vedle sebe řetězit (výstup Co jedné sčítačky propojit se vstupem Ci další) a provádět tak sčítání vícebitových čísel (viz níže).[1][2]
Booleovský zápis:
Pravdivostní tabulka úplné sčítačky:
| vstup | výstup | |||
|---|---|---|---|---|
| Ci | B | A | Co | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Vícebitové sčítačky
Čtyřbitová sčítačka s přenosem
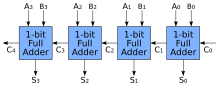
N-bitová sčítačka s přenosem jednoduše (odkazuje na Ripple carry adder, zkr. RCA) vzniká pouhým zřetězením n 1bitových sčítaček s přenosem, propojením výstupu Co sčítačky n-tý bit vstupu Ci sčítačky (n+1)-tého bitu (viz obrázek). Vstupem výsledné n-bitové sčítačky jsou pak dvě n-bitová čísla (+ případný přenos z předcházejícího bitu (nižšího řádu)), výstupem je jejich součet, široký n+1 bitů (n bitů + přenos). Název je odvozen z principu – příznak přenosu se propaguje (šíří) z jednoho bitu do druhého.
Sčítačka s podporou přenosu je jednoduchá na návrh a provedení a teoreticky je rozšiřitelná na libovolný počet bitů. Má však zásadní nevýhodu: s rostoucí šířkou (a tedy počtem zřetězených sčítaček s přenosem) přímo úměrně zvyšuje celkové zpoždění (doba ustálení) výsledného obvodu. Signál přenosu prochází v každé z sčítaček dvěma hradly, takže např. u 32bitové sčítačky se objeví správné hodnoty na výstupu se zpožděním až 64 pod-hradlových zpoždění, což může výrazně omezit propustnost (maximální možný počet sčítání za jednotku času) sekvenčního zařízení využívajícího tento typ sčítačky. Toto omezení vedlo ke snaze navrhnout n-bitovou sčítačku s menším zpožděním.
Sčítačka s předpovědí přenosu
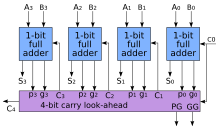
Sčítačka s predikcí přenosu jednoduše odkazuje na Carry Lookahead Adder, zkr. CLA) je n-bitová binární sčítačka schopná vypočítat součet za kratší dobu (v jednotkách hradlového zpoždění) než sčítačka s podporou přenosu (RCA). V RCA musí každá dílčí 1bitová sčítačka "čekat" na správný příznak přenosu bitu ze sčítačky nižšího řádu). Při CLA je (v podstatě) veškerý provoz mezi řády vypočítán ve stejné době – kombinačním obvodem jménem jednotka predikce přenosu (v Lookahead Carry Unit, zkr. LCU).
Výhody:
- výpočet součtu se zpožděním teoreticky nezávislým na šířce vstupních – O(), zatímco sčítačka s podporou přenosu má zpoždění přímo úměrná šířce vstupu – O()
Nevýhody:
- vyšší nároky na celkový počet hradel – O() a celkový počet tranzistorů O((vzhledem k potřebě hradel s počtem vstupů úměrných šířce sčítačky ve srovnání se sčítačkou s přenosem (O() hradel)
- od určitého počtu bitů přestává být prakticky realizovatelná (kvůli počtu hradel a výrobním omezením počtu vstupů na jedno hradlo). Široké sčítačky je proto třeba realizovat na více úrovních – kombinováním sčítaček na principu predikce přenosu (na nižší úrovni) a s podporou přenosu (na vyšší úrovni), nebo případně pomocí principu predikce přenosu na dvou (nebo více) úrovních.
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Binárna sčítačka na slovenské Wikipedii.
- ↑ Archivovaná kopie [online]. [cit. 2018-01-22]. Dostupné v archivu pořízeném dne 2012-01-05.
- ↑ [cit. 2018-01-22]. Dostupné online.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu binární sčítačka na Wikimedia Commons
Obrázky, zvuky či videa k tématu binární sčítačka na Wikimedia Commons



