Giniho koeficient

Giniho koeficient je číselná charakteristika diverzifikace. Využívá se zejména k vyjádření rozložení bohatství ve společnosti. Zároveň je často užívaným indexem příjmové nebo důchodové nerovnosti ve společnosti. Nejčastěji se uplatňuje v ekonomii, demografii či sociologii. Nabývá hodnot od nuly do jedné.
Giniho koeficient vynásobený stem nazýváme Giniho index.
Historie
Giniho koeficient byl poprvé představen italským statistikem, sociologem a demografem Corradem Ginim v roce 1912 v jeho článku "Variabilita a proměnlivost" (italsky Variabilità e mutabilità[1]), který publikoval v době, kdy působil jako ředitel statistického ústavu na Cagliarské univerzitě v Sardinii. Svoje výpočty založil na Lorenzově křivce, které byla představena v roce 1905 americkým ekonomem Maxem Lorenzem.
Definice
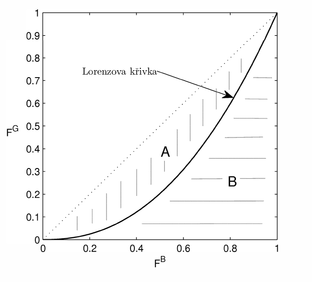
Zjednodušeně můžeme Giniho index graficky definovat na jednotkovém čtverci pomocí Lorenzovy křivky, která označuje poměr kumulativního bohatství spodních x procent populace k celkovému bohatství (obvykle zobrazovaném na ose y). Přímka se sklonem 45 stupňů (diagonála) tedy zobrazuje perfektní rozložení příjmů. Giniho koeficient je definován jako poměr obsahu plochy mezi přímkou znázorňující perfektní rozdělení příjmů a Lorenzovou křivkou (A) ku celkovému obsahu oblasti pod křivkou perfektního rozdělení (A + B). Tedy:
Protože obsah plochy pod diagonálou je polovina jednotkového čtverce, můžeme definici přepsat jako GC = 2A nebo také GC = 1 − 2B. Odtud použitím posledního jmenovaného výrazu dostáváme matematický vztah
kde a jsou distribuční funkce dobrých a špatných klientů (viz skóringový model). Jiné vyjádření získáme, vyjdeme-li ze vztahu GC=2A. Potom
Alternativním a také matematicky přesnějším způsobem definice Giniho koeficientu je metoda „poloviny relativního absolutního rozdílu“, který je matematickým ekvivalentem Lorenzovy křivky.
kde se předpokládá kladnost prvků xi (pouhý předpoklad xi0 není matematicky dostačující). Po provedení série úprav můžeme předchozí rovnici upravit do tvaru:
který značně zjednodušuje výpočet Giniho koeficientu zejména při použití výpočetní techniky.[2]
Vlastnosti
Giniho koeficient má mnoho vlastností, které z něj dělají vhodný nástroj k měření rozptylu a nerovností ve společnosti. Jedná se o statistiku vyjádřenou poměrem, což značně zjednodušuje jeho interpretaci. Rovněž se neodkazuje na průměr a jiné statistické výstupy (například příjem na člověka nebo hrubý domácí produkt). Dají se s ním tedy srovnávat různorodé skupiny, od zemí, přes regiony až po menší oblasti, ale i například pohlaví nebo etnické skupiny. Pomocí Giniho indexu jde tyto skupiny porovnávat i v čase, což umožňuje sledovat historický vývoj nerovností a predikovat vývoj budoucí.
Kromě toho je Giniho koeficient anonymní. Není tedy nutné přesně identifikovat každého jedince[3]. Další důležitou vlastností je jeho nezávislost na měřítku. Nebere se zde v úvahu velikost ekonomiky, ani měřítko výše mzdy. Nezáleží ani na velikosti populace.[4] Přesto by ovšem tyto informace měly být vzaty do úvahy při interpretaci koeficientu.
Z matematického hlediska nabývá koeficient hodnoty mezi 0 a 1, kde 1 značí absolutní nerovnost ve společnosti. Naopak hodnota 0 značí perfektní rozložení příjmů ve společnosti.[5] Obě tyto hodnoty jsou ovšem v realitě nedosažitelné. Hodnoty koeficientu se tedy zpravidla vyskytují někde mezi nimi. Pokud nabývá záporných hodnot značí to opačnou klasifikaci skóringové funkce. Pokud je řeč o Giniho indexu, ten nabývá hodnot od 0 do 100, kde 0 opět značí perfektní rovnost a 100 značí absolutní nerovnost.
Využití
Nejčastěji se Giniho koeficient využívá v ekonomii, kde se pomocí něho měří příjmová nerovnost nebo nerovnost rozložení bohatství ve společnosti. Můžeme počítat jak Giniho index z tržních příjmů (příjmů před zdaněním) a tedy bez účinku státních sociálních a daňových politik, tak z disponibilního důchodu (po zdanění a započítání transferů). Tyto hodnoty pak můžeme využít k evaluaci státní sociální politiky a daňových dopadů.
V sociologii se pak používá nejčastěji k odhadu nerovnosti přístupu ke vzdělání a příležitostem. Často se také využívá k měření míry diskriminace.
Přestože je Giniho koeficient nejvíc používaný v ekonomii a sociologii, může být užitečný i v ostatních vědních disciplínách zkoumajících distribuci. Ve zdravotnictví ho lze využít k měření nerovnosti zdraví a kvality života v populaci. V chemii byl použit například k vyjádření selektivity inhibitorů proteinů kinázy proti panelu kináz.[6] Ve školství může být použito ke změření rozdílů mezi univerzitami.[7] V ekologii se využívá k měření biologické rozmanitosti. Někdy se užívá k měření diskriminačních sil ratingových systémů při řízení úvěrového rizika.
Země dle Giniho koeficientu příjmové nerovnosti
Česká republika
Giniho koeficient příjmové nerovnosti v České republice patří mezi velmi nízké. Dlouhodobě se pohybuje těsně nad 0,2 podobně jako v sousedním Slovensku a Polsku, přesto v posledních letech díky ekonomickému rozvoji zaznamenává lehký nárůst v souladu s celosvětovým trendem[8]. V roce 2017 jeho hodnota podle Světové banky dosahovala 0,247.[9]
Evropa
V Evropě se koeficient příjmové nerovnosti v letech 2015–2019 pohyboval mezi 0,2 a 0,4. Mezi země s nejrovnoměrněji rozloženými příjmy patřily Slovensko, Slovinsko, Česko či Island. Naopak vysoká nerovnost příjmů byla například v Bulharsku, Litvě, Spojeném království či Lotyšsku.[10]
Svět

Vysokých hodnot dosahují zejména státy jižní Afriky a Jižní Ameriky. Vůbec nejvyšší koeficient z měřených zemí je zaznamenáván u Jihoafrické republiky, kde dokonce přesahuje hodnotu 0,6. Na opačném konci spektra pak najdeme zejména státy Evropy.[10] Podrobnější rozložení koeficientu lze odhadnout ze snímků z kosmu.[11] S růstem velikosti měst roste i nerovnost jejich obyvatel.[12]
Odhad Giniho koeficientu
Somersovo d
Pro odhad Giniho koeficientu lze v praxi použít více postupů. Jedním z často používaných je odhad pomocí tzv. Somersovy d statistiky.
Označíme-li skóre j-tého klienta, můžeme definovat charakteristiky a, b a c následovně:
- a je počet všech dvojic klientů (i, j), i > j takových, že rozdíly a jsou nenulové a mají stejné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen větším skóre než špatný klient);
- b je počet všech dvojic klientů (i,i, j), i > j takových, že rozdíly a jsou nenulové a mají opačné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen menším skóre než špatný klient);
- c je počet všech dvojic klientů (i, j), i > j takových, že a (tedy takových dvojic, kde dobrý klient byl ohodnocen stejným skóre jako špatný klient).
Potom Somersovu d statistiku spočítáme jako
Výpočet Giniho koeficientu v jeho prosté (nevážené) i vážené formě je možno provést např. pomocí volně dostupné aplikace EasyStat.[13]
Reference
- ↑ CERIANI, Lidia; VERME, Paolo. The origins of the Gini index: extracts from Variabilità e Mutabilità (1912) by Corrado Gini. The Journal of Economic Inequality. 2011-06-10, roč. 10, čís. 3, s. 421–443. Dostupné online [cit. 2020-04-24]. ISSN 1569-1721. DOI 10.1007/s10888-011-9188-x.
- ↑ GENČEV, Marian; MUSILOVÁ, Denisa; ŠIROKÝ, Jan. A Mathematical Model of the Gini Coefficient and Evaluation of the Redistribution Function of the Tax System in the Czech Republic. Politická ekonomie. 2018-12-01, roč. 66, čís. 6, s. 732–750. Dostupné online [cit. 2020-04-28]. DOI 10.18267/j.polek.1232.
- ↑ FERREIRA, F. H. G.; LITCHFIELD, J. A. Calm After the Storms: Income Distribution and Welfare in Chile, 1987-94. The World Bank Economic Review. 1999-09-01, roč. 13, čís. 3, s. 509–538. Dostupné online [cit. 2020-04-24]. ISSN 0258-6770. DOI 10.1093/wber/13.3.509.
- ↑ Agricultural production index by region. dx.doi.org [online]. 2009-07-28 [cit. 2020-04-24]. Dostupné online.
- ↑ is.mendelu.cz [online]. [cit. 2020-04-28]. Dostupné online.
- ↑ Graczyk, Piotr (2007). "Gini Coefficient: A New Way To Express Selectivity of Kinase Inhibitors against a Family of Kinases". Journal of Medicinal Chemistry. 50 (23): 5773–5779. doi:10.1021/jm070562u. PMID 17948979.
- ↑ HALFFMAN, Willem; LEYDESDORFF, Loet. Is Inequality Among Universities Increasing? Gini Coefficients and the Elusive Rise of Elite Universities. Minerva. 2010-03, roč. 48, čís. 1, s. 55–72. Dostupné online [cit. 2020-04-28]. ISSN 0026-4695. DOI 10.1007/s11024-010-9141-3. (anglicky)
- ↑ ODSTRAŇOVÁNÍ NEROVNOSTÍ [online]. Evropská komise [cit. 2020-04-28]. Dostupné online.
- ↑ GINI index (World Bank estimate) | Data. data.worldbank.org [online]. [cit. 2020-04-28]. Dostupné online.
- ↑ a b Income inequality. [s.l.]: [s.n.] Dostupné online. DOI 10.1787/459aa7f1-en (accessed on 28 april 2020). (anglicky) Type: dataset DOI: 10.1787/459aa7f1-en.
- ↑ MIRZA, M. Usman; XU, Chi; BAVEL, Bas van; VAN NES, Egbert H.; SCHEFFER, Marten. Global inequality remotely sensed. S. e1919913118. Proceedings of the National Academy of Sciences [online]. 2021-05-04. Roč. 118, čís. 18, s. e1919913118. Dostupné online. DOI 10.1073/pnas.1919913118. (anglicky)
- ↑ Study: As cities grow in size, the poor 'get nothing at all'. phys.org [online]. 2021-08-17 [cit. 2022-01-24]. Dostupné online. (anglicky)
- ↑ NOVOTNÝ, Josef; NOSEK, Vojtěch; JELÍNEK, Karel. EasyStat 1.0 – Uživatelský manuál [online]. Praha: Přírodovědecká fakulta UK, 2014. Dostupné online.
Související články
- Diverzifikace
- Kreditní riziko
- Lorenzova křivka
- Paretův princip
- Skóringový model
- Ekonomie
- Ekonomická nerovnost
- Corrado Gini
- Gatsbyho křivka
Externí odkazy
 Obrázky, zvuky či videa k tématu Giniho koeficient na Wikimedia Commons
Obrázky, zvuky či videa k tématu Giniho koeficient na Wikimedia Commons - Giniho koeficient na www.finance-management.cz
- http://finmag.penize.cz/ekonomika/266516-fetis-cisel-jak-nemerit-nerovnost













