Hasseův diagram

V matematické disciplíně teorie uspořádání se používá Hasseův diagram (pojmenovaný po Helmutu Hasseovi) k zobrazení konečné částečně uspořádané množiny. Konkrétně pro uspořádanou množinu (S,≤) reprezentujeme v Hasseově diagramu každý prvek množiny S jako vrchol grafu. Dva vrcholy se spojí čarou (hranou) vedenou zdola nahoru od x k y, jestliže x < y a neexistuje takové z, že x < z < y (zde je < binární relace získaná z ≤ odejmutím prvků (x,x) pro každé x). Říkáme také, že y pokrývá x nebo že y je bezprostřední předchůdce prvku x. Vrcholy grafu musí být umístěny tak, aby každá hrana spojovala právě dva vrcholy.

Příklady

  • Množina A = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 } všech dělitelů čísla 60 částečně uspořádaná podle dělitelnosti může být zobrazena následujícím Hasseovým diagramem:
Svaz dělitelů čísla 60
Svaz dělitelů čísla 60

S = {a,b,c,d}

       

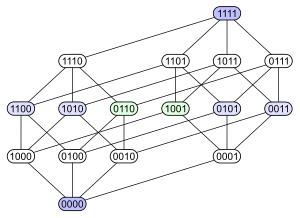Externí odkazy