Universelle Eigenschaft
Eine universelle Eigenschaft ist eine Methode der Mathematik, und dort insbesondere der abstrakten Algebra, sich eine gewünschte Struktur ohne Angabe einer konkreten Konstruktion zu verschaffen. Dabei wird für Objekte einer bestimmten Kategorie , z. B. der Kategorie der abstrakten Algebren, eine Eigenschaft festgelegt, z. B., dass es von einem Vektorraum eine injektive Abbildung in die Algebra gebe.
Die Universalkonstruktion besteht nun darin, die Existenz eines „kleinsten“ Elements der Kategorie zu behaupten, das die Eigenschaft erfüllt. Im Beispiel wäre das die Tensoralgebra von . „Kleinstes“ zu sein bedeutet, dass es zu jedem Objekt der Kategorie , das die geforderte Eigenschaft erfüllt, einen eindeutig bestimmten Morphismus gibt, der mit der Eigenschaft verträglich ist, im Beispiel mit der Einbettung von vertauscht.
Das „kleinste“ Element muss nicht eindeutig bestimmt sein, jedoch sind alle „kleinsten“ Elemente, sofern existent, isomorph. Als Existenzbeweis kann eine konkrete Konstruktion angegeben werden, jedoch sind die Details so einer Konstruktion für die Theorie der Struktur meistens unwesentlich.
Beispiele
- Der kanonische Homomorphismus einer Gruppe auf die Faktorgruppe nach einem Normalteiler
- Die Tensoralgebra, siehe oben
- Der Kern einer linearen Abbildung
- Die lineare Hülle einer Teilmenge eines Vektorraums als kleinster Unterraum, der diese Menge enthält
- Die affine Hülle einer Teilmenge eines affinen Raums
- Die konvexe Hülle einer Teilmenge eines affinen Raums
- Der algebraische Abschluss eines Körpers
- Die freie Termalgebra
- Die abgeschlossene Hülle einer Teilmenge eines topologischen Raums
- Das Innere einer Teilmenge eines topologischen Raums als größte offene Menge, die in der Teilmenge enthalten ist
Motivation
Wofür sind universelle Eigenschaften gut? Wenn eine gewisse Konstruktion eine universelle Eigenschaft erfüllt, so ergeben sich daraus weitere Erkenntnisse:
- Universelle Eigenschaften definieren Objekte bis auf Isomorphismen. Zu zeigen, dass zwei Objekte dieselbe universelle Eigenschaft erfüllen, ist somit eine mögliche Strategie, um deren Isomorphie zu zeigen.
- Die genauen Details der gegebenen Konstruktion sind möglicherweise komplex und äußerst technischer Natur, aber dank der universellen Eigenschaft kann man all diese Details vergessen: Alles, was man über das Konstrukt wissen muss, ist bereits in der universellen Eigenschaft enthalten. Wenn man die universelle Eigenschaft anstelle der konkreten Details verwendet, macht dies einen Beweis meist kurz und elegant.
- Sofern die universelle Konstruktion für jedes Objekt einer Kategorie durchgeführt werden kann, so erhalten wir einen Funktor in die Zielkategorie.
- Dieser Funktor ist obendrein rechts- oder linksadjungiert zu einem gegebenen Funktor. Aber solche Funktoren vertauschen grundsätzlich mit Kolimites bzw. Limites. Auf diese Weise folgt beispielsweise sofort, dass der Kern des direkten Produktes zweier linearer Abbildungen dem Produkt der Kerne gleicht (kanonisch isomorph ist).
Formale Definition
Sei ein Funktor von der Kategorie in die Kategorie und sei ein Objekt von . Ein universeller Morphismus von nach besteht aus einem Paar , wobei ein -Objekt und ein Morphismus in ist, sodass die folgende universelle Eigenschaft erfüllt ist:
- Für jedes -Objekt und jeden -Morphismus gibt es genau einen Morphismus , sodass gilt, d. h., sodass das folgende Diagramm kommutiert:
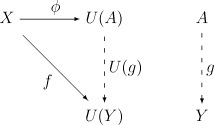
Intuitiv bedeutet die Existenz von , dass „allgemein genug“ ist, während die Eindeutigkeit sicherstellt, dass nicht „zu allgemein“ ist. Man kann in dieser Definition auch sämtliche Pfeile umkehren, d. h. das kategorientheoretische Dual betrachten. Ein universeller Morphismus von nach ist ein Paar , wobei ein -Objekt und ein Morphismus in ist, sodass die folgende universelle Eigenschaft erfüllt ist:
- Für jedes -Objekt und jeden -Morphismus gibt es genau einen Morphismus , sodass gilt, d. h., sodass das folgende Diagramm kommutiert:
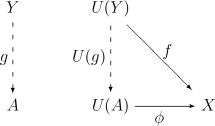
Eigenschaften
Existenz und Eindeutigkeit
Die bloße Definition garantiert noch keine Existenz. Zu einem Funktor und einem Objekt wie oben kann ein universeller Morphismus von nach existieren oder auch nicht. Falls jedoch ein universeller Morphismus existiert, so ist er bis auf Isomorphie eindeutig bestimmt. Ist also ein weiteres solches Paar, so gibt es einen Isomorphismus mit . Dies erkennt man leicht, indem man die Definition der universellen Eigenschaft auf anwendet.
Äquivalente Formulierungen
Die Definition eines universellen Morphismus kann man auf verschiedene Weise formulieren. Mit einem Funktor und einem -Objekt sind die folgenden Aussagen äquivalent:
- ist ein universeller Morphismus von nach .
- ist ein Anfangsobjekt der Kommakategorie .
- ist eine Darstellung des Funktors .
Entsprechend sind die dualen Aussagen äquivalent:
- ist ein universeller Morphismus von nach .
- ist ein Endobjekt der Kommakategorie .
- ist eine Darstellung des Funktors .
Beziehung zu adjungierten Funktoren
Sei ein universeller Morphismus von nach und einer von nach . Aufgrund der universellen Eigenschaft existiert zu jedem Morphismus genau ein Morphismus mit .
Gibt es sogar zu jedem Objekt der Kategorie einen universellen Morphismus nach , so definiert die Zuordnung , einen Funktor . Die Morphismen bilden eine natürliche Transformation von (dem Identitätsfunktor auf ) nach . Dann ist ein Paar adjungierter Funktoren, und zwar ist links-adjungiert zu und rechts-adjungiert zu .
Entsprechendes gilt mutatis mutandis im dualen Fall.
Geschichte
Universelle Eigenschaften wurden im Zusammenhang mit verschiedenen topologischen Konstruktionen 1948 von Pierre Samuel eingeführt. Später nutzte Nicolas Bourbaki sie in großem Umfang. Das eng verbundene Konzept der Adjungiertheit von Funktoren hat Daniel Kan unabhängig hiervon 1958 eingeführt.











































