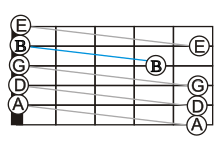
E-flat tuning

Guitar tunings are the assignment of pitches to the open strings of guitars, including classical guitars, acoustic guitars, and electric guitars. Tunings are described by the particular pitches that are made by notes in Western music. By convention, the notes are ordered and arranged from the lowest-pitched string (i.e., the deepest bass-sounding note) to the highest-pitched string (i.e., the highest sounding note), or the thickest string to thinnest, or the lowest frequency to the highest.[1] This sometimes confuses beginner guitarists, since the highest-pitched string is referred to as the 1st string, and the lowest-pitched is the 6th string.
Standard tuning defines the string pitches as E (82.41 Hz), A (110 Hz), D (146.83 Hz), G (196 Hz), B (246.94 Hz), and E (329.63 Hz), from the lowest pitch (low E2) to the highest pitch (high E4). Standard tuning is used by most guitarists, and frequently used tunings can be understood as variations on standard tuning. To aid in memorising these notes, mnemonics are used, for example, Eddie Ate Dynamite Good Bye Eddie.[2]
The term guitar tunings may refer to pitch sets other than standard tuning, also called nonstandard, alternative, or alternate.[3] There are hundreds of these tunings, often with small variants of established tunings. Communities of guitarists who share a common musical tradition often use the same or similar tuning styles.
Standard and alternatives
Standard
Standard tuning is the tuning most frequently used on a six-string guitar and musicians assume this tuning by default if a specific alternate (or scordatura) is not mentioned. In scientific pitch notation,[4] the guitar's standard tuning consists of the following notes: E2–A2–D3–G3–B3–E4 .
String frequencies
of standard tuningString Frequency Scientific
pitch
notation1 (E) 329.63 Hz E4 2 (B) 246.94 Hz B3 3 (G) 196.00 Hz G3 4 (D) 146.83 Hz D3 5 (A) 110.00 Hz A2 6 (E) 82.41 Hz E2
The guitar is a transposing instrument; that is, music for guitars is notated one octave higher than the true pitch. This is to reduce the need for ledger lines in music written for the instrument, and thus simplify the reading of notes when playing the guitar.[5]
Standard tuning provides reasonably simple fingering (fret-hand movement) for playing standard scales and basic chords in all major and minor keys. Separation of the second (B) through fifth (A) strings being tuned in minor 3rds and second (e) following the low (E) string as the separation being tuned in 5ths, and creating as by a five-semitone interval (a perfect fourth) allows the guitarist to play a chromatic scale with each of the four fingers of the fretting hand controlling one of the first four frets (index finger on fret 1, little finger on fret 4, etc.) only when the hand is in the first position.
The open notes of the second (B) and third (G) strings are separated by four semitones (a major third). This tuning pattern of (low) fourths, one major third, and one fourth was inherited by the guitar from its predecessor instrument, the viol. The irregular major third breaks the fingering patterns of scales and chords, so that guitarists have to memorize multiple chord shapes for each chord. Scales and chords are simplified by major thirds tuning and all-fourths tuning, which are regular tunings maintaining the same musical interval between consecutive open string notes.[3]
When barring each fret in standard tuning, only and all of the notes of pentatonic scales are produced. For example, the open strings E, A, D, G, B, E yield the notes of the E minor pentatonic scale (G major pentatonic), and barring the third fret produces the notes of the G minor pentatonic scale (B♭ major pentatonic).
Chromatic note progression 0 I II III IV String open 1st fret
(index)2nd fret
(middle)3rd fret
(ring)4th fret
(little)6th E2 F2 F♯
2 / G♭
2G2 G♯
2 / A♭
25th A2 A♯
2 / B♭
2B2 C3 C♯
3 / D♭
34th D3 D♯
3 / E♭
3E3 F3 F♯
3 / G♭
33rd G3 G♯
3 / A♭
3A3 A♯
3 / B♭
3B3 2nd B3 C4 C♯
4 / D♭
4D4 D♯
4 / E♭
41st E4 F4 F♯
4 / G♭
4G4 G♯
4 / A♭
4
Alternative
Alternative ("alternate") tuning refers to any open string note arrangement other than standard tuning. These offer different kinds of deep or ringing sounds, chord voicings, and fingerings on the guitar. Alternative tunings are common in folk music. Alternative tunings change the fingering of common chords when playing the guitar, and this can ease the playing of certain chords while simultaneously increase the difficulty of playing other chords.
Some tunings are used for particular songs and may be named after the song's title. There are hundreds of these tunings, although many are slight variations of other alternate tunings.[6] Several alternative tunings are used regularly by communities of guitarists who share a common musical tradition, such as American folk or Celtic folk music.[7]
The various alternative tunings have been grouped into the following categories:[8]
- dropped[9][10]
- open[11]
- both major and minor (cross note)[12][10][13]
- modal[10][14]
- instrumental (based on other stringed instruments)
- miscellaneous ("special").[10][13][15]
Joni Mitchell developed a shorthand to specify guitar tunings: one letter naming the note of the open lowest string, followed by the relative fret (half-step) offsets between adjacent strings; in this format, the standard tuning is E55545.[16] This scheme highlights pitch relationships and simplifies comparisons among different tuning schemes.
String gauges
String gauge refers to the thickness and diameter of a guitar string, which influences the overall sound and pitch of the guitar depending on the guitar string used.[17] Some alternative tunings are difficult or even impossible to achieve with conventional guitars due to the sets of guitar strings, which have gauges optimized for standard tuning. With conventional sets of guitar strings, some higher tunings increase the string-tension until playing the guitar requires significantly more finger-strength and stamina, or even until a string snaps or the guitar is warped. However, with lower tunings, the sets of guitar strings may be loose and buzz. The tone of the guitar strings is also negatively affected by using unsuitable string gauges on the guitar.
Generally, alternative tunings benefit from re-stringing of the guitar with string gauges purposefully chosen to optimize particular tunings[18] by using lighter strings for higher-pitched notes (to lower the tension of the strings) and heavier strings for lower-pitched notes (to prevent string buzz and vibration).
Dropped tunings
A dropped tuning is one of the categories of alternative tunings and the process starts with standard tuning and typically lowers the pitch of ("drops") one or more strings, almost always the lowest-pitched (E) string on the guitar.
The drop D tuning is common in electric guitar and heavy metal music.[19] The low E string is tuned down one whole step (to D) and the rest of the strings remain in standard tuning. This creates an "open power chord" (three-note fifth) with the low three strings (DAD).
Although the drop D tuning was introduced and developed by blues and classical guitarists, it is well known from its usage in contemporary heavy metal and hard rock bands. Early hard rock songs tuned in drop D include the Beatles' "Dear Prudence" (1968) and Led Zeppelin's "Moby Dick" (1969).[20] Tuning the lowest string one tone down, from E to D, allowed these musicians to acquire a heavier and darker sound than in standard tuning. Without needing to tune all strings (Standard D tuning), they could tune just one, in order to lower the key. Drop D is also a convenient tuning, because it expands the scale of an instrument by two semitones: D and D♯.
In the mid-1980s, three alternative rock bands, King's X, Soundgarden and Melvins, influenced by Led Zeppelin and Black Sabbath, made extensive use of drop D tuning. While playing power chords (a chord that includes the prime, fifth and octave) in standard tuning requires a player to use two or three fingers, drop D tuning needs just one, similar in technique to playing barre chords. This allowed them to use different methods of articulating power chords (legato for example) and more importantly, it allowed guitarists to change chords faster. This new technique of playing power chords introduced by these early grunge bands was a great influence on many artists, such as Rage Against the Machine and Tool. The same drop D tuning then became common practice among alternative metal acts such as the band Helmet, who used the tuning a great deal throughout their career and would later influence much alternative metal and nu metal bands.[21]
There also exists double drop D tuning, in which both E strings are down-tuned a whole step (to D). The rest of the strings keep their original pitch.
Open tunings

An open tuning allows the guitarist to play a chord by strumming the open strings (no strings fretted).
Open tunings may be chordal or modal. In chordal open tunings, the open chord consists of at least three different pitch classes. In a given key, these are the root note, its 3rd and its 5th, and may include all the strings or a subset. The tuning is named for the base chord when played open, typically a major chord, and all similar chords in the chromatic scale are played by barring all strings across a single fret.[22] Open tunings are common in blues and folk music.[23] These tunings are frequently used in the playing of slide and lap-slide ("Hawaiian") guitars, and Hawaiian slack key music.[22][24] A musician who is well known for using open tuning in his music is Ry Cooder, who uses open tunings when playing the slide guitar.[23]
Most modern music uses equal temperament because it facilitates the ability to play the guitar in any key—as compared to just intonation, which favors certain keys, and makes the other keys sound less in tune.[25]
Repetitive open tunings are used for two classical non-Spanish guitars. For the English guitar, the open chord is C major (C–E–G–C–E–G);[26] for the Russian guitar, which has seven strings, it is G major (D–G–B–D–G–B–D).[27][28]
When the open strings constitute a minor chord, the open tuning may sometimes be called a cross-note tuning.
Major key tunings


Major open tunings give a major chord with the open strings.
Open tunings Major triad Repetitive Overtones Other
(often most popular)
Open A (A,C♯,E) A–C♯–E–A–C♯–E A–A–E–A–C♯–E E–A–C♯–E–A–E Open B (B,D♯,F♯) B–D♯–F♯–B–D♯–F♯ B–B–F♯–B–D♯–F♯ B–F♯–B–F♯–B–D♯ Open C (C,E,G) C–E–G–C–E–G C–C–G–C–E–G C–G–C–G–C–E Open D (D,F♯,A) D–F♯–A–D–F♯–A D–D–A–D–F♯–A D–A–D–F♯–A–D Open E (E,G♯,B) E–G♯–B–E–G♯–B E–E–B–E–G♯–B E–B–E–G♯–B–E Open F (F,A,C) F–A–C–F–A–C F–F–C–F–A–C C–F–C–F–A–F Open G (G,B,D) G–B–D–G–B–D G–G–D–G–B–D D–G–D–G–B-D
Open tunings often tune the lowest open note to C, D, or E and they often tune the highest open note to D or E; tuning down the open string from E to D or C avoids the risk of breaking strings, which is associated with tuning up strings.
Open D
The open D tuning (D–A–D–F♯–A–D), also called "Vestapol" tuning,[29] is a common open tuning used by European and American/Western guitarists working with alternative tunings. The Allman Brothers Band instrumental "Little Martha" used an open D tuning raised one half step, giving an open E♭ tuning with the same intervallic relationships as open D.[30]
Open C
The English guitar used a repetitive open C tuning (with distinct open notes C–E–G–C–E–G) that approximated a major-thirds tuning.[26] This tuning is evident in William Ackerman's song "Townsend Shuffle", as well as by John Fahey for his tribute to Mississippi John Hurt.[31][32]
The C–C–G–C–E–G tuning uses some of the harmonic sequence (overtones) of the note C.[33][34] This overtone-series tuning was modified by Mick Ralphs, who used a high C note rather than the high G note for "Can't Get Enough" on Bad Company. Ralphs said, "It needs the open C to have that ring," and "it never really sounds right in standard tuning".[35]
Open G
Mick Ralphs' open C tuning was originally an open G tuning, which listed the initial six overtones of the G note, namely G–G–D–G–B–D; Ralphs used this open G tuning for "Hey Hey" and while writing the demo of "Can't Get Enough".[35]
Open-G tuning usually refers to D–G–D–G–B–D. The open G tuning variant G–G–D–G–B–D was used by Joni Mitchell for "Electricity", "For the Roses" and "Hunter (The Good Samaritan)".[36] Truncating this tuning to G–D–G–B–D for his five-string guitar, Keith Richards uses this overtones-tuning on the Rolling Stones's "Honky Tonk Women", "Brown Sugar" and "Start Me Up".[37]
The seven-string Russian guitar uses the open G tuning D–G–B–D–G–B–D, which contains mostly major and minor thirds.[38][28]
Creating any kind of open tuning
Any kind of chordal tuning can be achieved, simply by using the notes in the chord and tuning the strings to those notes. For example, Asus4 has the notes A, D, E. By tuning the strings to only those notes, it creates a chordal Asus4 tuning.
Power chord (fifths) open tunings:[39] A5 E–A–E–A–A–E B5 F♯–B–F♯–B–B–F♯ C5 C–G–C–G–G–G D5 D–A–D–A–D–D E5 E–B–E–E–B–E F5 F–C–C–C–C–F G5 D–G–D–G–D–G
Bass players may omit the last two strings.
Minor or "cross-note" tunings
Cross-note tunings include a minor third, so giving a minor chord with open strings. Fretting the minor-third string at the first fret produces a major-third, so allowing a one-finger fretting of a major chord.[40] By contrast, it is more difficult to fret a minor chord using an open major-chord tuning.
Bukka White and Skip James[41] are well known for using cross-note E-minor (E B E G B E) in their music, as in 'Hard Time Killin Floor Blues'.
Other open chordal tunings
Some guitarists choose open tunings that use more complex chords, which gives them more available intervals on the open strings. C6, E6, E7, E6/9 and other such tunings are common among lap-steel players such as Hawaiian slack-key guitarists and country guitarists, and are also sometimes applied to the regular guitar by bottleneck (a slide repurposed from a glass bottle) players striving to emulate these styles. A common C6 tuning, for example, is C–E–G–A–C–E, which provides open major and minor thirds, open major and minor sixths, fifths, and octaves. By contrast, most open major or open minor tunings provide only octaves, fifths, and either a major third/sixth or a minor third/sixth—but not both. Don Helms of Hank Williams band favored C6 tuning; slack-key artist Henry Kaleialoha Allen uses a modified C6/7 (C6 tuning with a B♭ on the bottom); Harmon Davis favored E7 tuning; David Gilmour has used an open G6 tuning.
Modal tunings
Modal tunings are open tunings in which the open strings of the guitar do not produce a tertian (i.e., major or minor, or variants thereof) chord. The strings may be tuned to exclusively present a single interval (all fourths; all fifths; etc.) or they may be tuned to a non-tertian chord (unresolved suspensions such as E–A–B–E–A–E, for example). Modal open tunings may use only one or two pitch classes across all strings (as, for example, some metal guitarists who tune each string to either E or B, forming "power chords" of ambiguous major/minor tonality).
Popular modal tunings include D Modal (D-G-D-G-B-E) and C Modal (C-G-D-G-B-D).
Lowered (standard)
Derived from standard EADGBE, all the strings are tuned lower by the same interval, thus providing the same chord positions transposed to a lower key. Lower tunings are popular among rock and heavy metal bands. The reason for tuning down below the standard pitch is usually either to accommodate a singer's vocal range or to get a deeper/heavier sound or pitch.[42] Common examples include:
E♭ tuning
Rock guitarists (such as Jimi Hendrix on the songs "Voodoo Child (Slight Return)" and "Little Wing") occasionally tune all their strings down by one semitone to obtain E♭ tuning. This makes the strings easier to bend when playing and with standard fingering results in a lower key. It also facilitates E shape fingerings when playing with horn instruments.[43] Grunge band Nirvana also used this tuning extensively throughout their career, most significantly in their albums Bleach and In Utero.
D tuning

D Tuning, also called One Step Lower, Whole Step Down, Full Step or D Standard, is another alternative. Each string is lowered by a whole tone (two semitones) resulting in D-G-C-F-A-D. It is used mostly by heavy metal bands to achieve a heavier, deeper sound, and by blues guitarists, who use it to accommodate string bending and by 12-string guitar players to reduce the mechanical load on their instrument. Among musicians, Elliott Smith was known to use D tuning as his main tuning for his music. It was also used for several songs on the Velvet Underground's album The Velvet Underground & Nico. Metal band Megadeth has also been using this tuning since their album Dystopia to facilitate frontman Dave Mustaine's age and voice after his battle with throat cancer.
Regular tunings
| Regular tunings | |
|---|---|
 For regular guitar-tunings, the distance between consecutive open strings is a constant musical-interval, measured by semitones on the chromatic circle. The chromatic circle lists the twelve notes of the octave. | |
| Basic information | |
| Aliases | Uniform tunings |
| Advanced information | |
| Advantages | Simplifies learning by beginners and improvisation by advanced guitarists |
| Disadvantages | Replicating the open chords ("cowboy chords") of standard tuning is difficult; intermediate guitarists must relearn the fretboard and chords. |
| Regular tunings (semitones) | |
| Trivial (0) | |
| Minor thirds (3) | |
| Major thirds (4) | |
| All fourths (5) | |
| Augmented fourths (6) | |
| New standard (7, 3) | |
| All fifths (7) | |
| Minor sixths (8) | |
| Guitar tunings | |
In standard tuning, there is an interval of a major third between the second and third strings, and all the other intervals are fourths. The irregularity has a price. Chords cannot be shifted around the fretboard in the standard tuning E–A–D–G–B–E, which requires four chord-shapes for the major chords. There are separate chord-forms for chords having their root note on the third, fourth, fifth, and sixth strings.[44] These are called inversions.
In contrast, regular tunings have equal intervals between the strings,[45] and so they have symmetrical scales all along the fretboard. This makes it simpler to translate chords. For the regular tunings, chords may be moved diagonally around the fretboard. The diagonal movement of chords is especially simple for the regular tunings that are repetitive, in which case chords can be moved vertically: Chords can be moved three strings up (or down) in major-thirds tuning, and chords can be moved two strings up (or down) in augmented-fourths tuning. Regular tunings thus appeal to new guitarists and also to jazz-guitarists, whose improvisation is simplified by regular intervals.
On the other hand, five- and six-string open chords ("cowboy chords") are more difficult to play in a regular tuning than in standard tuning. Instructional literature uses standard tuning.[46] Traditionally a course begins with the hand in first position,[47] that is, with the left-hand covering frets 1–4.[48] Beginning players first learn open chords belonging to the major keys C, G, and D. Guitarists who play mainly open chords in these three major-keys and their relative minor-keys (Am, Em, Bm) may prefer standard tuning over many regular tunings,[49][50] On the other hand, minor-thirds tuning features many barre chords with repeated notes,[51] properties that appeal to acoustic-guitarists and beginners.
Major thirds and perfect fourths
Standard tuning mixes a major third (M3) with its perfect fourths. Regular tunings that are based on either major thirds or perfect fourths are used, for example, in jazz.
All fourths tuning E2–A2–D3–G3–C4–F4 keeps the lowest four strings of standard tuning, changing the major third to a perfect fourth.[52][53] Jazz musician Stanley Jordan stated that all-fourths tuning "simplifies the fingerboard, making it logical".[54]
Major-thirds tuning (M3 tuning) is a regular tuning in which the musical intervals between successive strings are each major thirds, for example E2–G♯2–C3–E3–G♯3–C4.[55][56][57][58] Unlike all-fourths and all-fifths tuning, M3 tuning repeats its octave after three strings, which simplifies the learning of chords and improvisation.[46] This repetition provides the guitarist with many possibilities for fingering chords.[55][58] With six strings, major-thirds tuning has a smaller range than standard tuning; with seven strings, the major-thirds tuning covers the range of standard tuning on six strings.[56][57][58]
Major-thirds tunings require less hand-stretching than other tunings, because each M3 tuning packs the octave's twelve notes into four consecutive frets.[56][59] The major-third intervals let the guitarist play major chords and minor chords with two three consecutive fingers on two consecutive frets.[60]
Chord inversion is especially simple in major-thirds tuning. The guitarist can invert chords by raising one or two notes on three strings—playing the raised notes with the same finger as the original notes. In contrast, inverting triads in standard and all-fourths tuning requires three fingers on a span of four frets.[61] In standard tuning, the shape of an inversion depends on the involvement of the major-third between the 2nd and 3rd strings.[62]
All fifths and "new standard tuning"

- C2–G2–D3–A3–E4–B4
All-fifths tuning is a tuning in intervals of perfect fifths like that of a mandolin or a violin; other names include "perfect fifths" and "fifths".[63] It has a wide range. Its implementation has been impossible with nylon strings and has been difficult with conventional steel strings. The high B makes the first string very taut, and consequently, a conventionally gauged string easily breaks.
Jazz guitarist Carl Kress used a variation of all-fifths tuning—with the bottom four strings in fifths, and the top two strings in thirds, resulting in B♭1–F2–C3–G3–B3–D4. This facilitated tenor banjo chord shapes on the bottom four strings and plectrum banjo chord shapes on the top four strings. Contemporary New York jazz-guitarist Marty Grosz uses this tuning.
All-fifths tuning has been approximated by the so-called "New Standard Tuning" (NST) of King Crimson's Robert Fripp, in which NST replaces all-fifths' high B4 with a high G4. To build chords, Fripp uses "perfect intervals in fourths, fifths and octaves", so avoiding minor thirds and especially major thirds,[64] which are slightly sharp in equal temperament tuning (in comparison to thirds in just intonation). It is a challenge to adapt conventional guitar-chords to new standard tuning, which is based on all-fifths tuning.[a] Some closely voiced jazz chords become impractical in NST and all-fifths tuning.[66]
Instrumental tunings
These are tunings in which some or all strings are retuned to emulate the standard tuning of some other instrument, such as a lute, banjo, cittern, mandolin, etc. Many of these tunings overlap other categories, especially open and modal tunings.
Miscellaneous or "special" tunings
This category includes everything that does not fit into any of the other categories, for example (but not limited to): tunings designated only for a particular piece; non-western intervals and modes; micro- or macro-tones (half sharps/flats, etc.); and "hybrid tunings" combining features of major alternate tuning categories – most commonly an open tuning with the lowest string dropped.[67]
See also
- Bass guitar tuning
- List of guitar tunings
- Music and mathematics
- Open G tuning
- Stringed instrument tunings
- DADGAD
Notes
- ^ Musicologist Eric Tamm wrote that despite "considerable effort and search I just could not find a good set of chords whose sound I liked" for rhythm guitar.[65]
Citation references
- ^ Denyer (1992, pp. 68–69)
- ^ Phillips, Mark; Chappell, Jon (2 October 2012). Guitar For Dummies, with DVD. John Wiley & Sons. p. 17. ISBN 978-1-118-11554-1. Retrieved 29 January 2024.
- ^ a b Brown, J. (2020). "11 alternate tunings every guitarist should know".
- ^ "Online guitar tuner". TheGuitarLesson.com. Archived from the original on 24 August 2013. Retrieved 27 August 2013.
- ^ "Transposing Instruments – Music Theory Academy". 18 January 2013. Retrieved 24 September 2019.
- ^ Weissman (2006, 'Off-the-wall tunings: A brief inventory' (Appendix A), pp. 95–96)
- ^ Caluda, Glenn (5 May 2014). "Open Tunings for Folk Guitar". The American Music Teacher. 63 (5): 54. Retrieved 1 November 2020.
- ^ Roche (2004, 'Categories of tunings', p. 153)
- ^ Roche (2004, pp. 153–156)
- ^ a b c d Denyer (1992, pp. 158–159)
- ^ Roche (2004, 'Open tunings', pp. 156–159)
- ^ Roche (2004, 'Cross-note tunings', p. 166)
- ^ a b Sethares (2011)
- ^ Roche (2004, 'Modal tunings', pp. 160–165)
- ^ Roche (2004, 'More radical tunings', p. 166)
- ^ "Notation". Joni Mitchell. Archived from the original on 15 March 2016. Retrieved 20 March 2016.
- ^ Faherty, Michael; Aaronson, Neil L. (1 October 2010). "Acoustical differences between treble guitar strings of different tension (i.e., gauge)". The Journal of the Acoustical Society of America. 128 (4): 2449. Bibcode:2010ASAJ..128.2449F. doi:10.1121/1.3508761. ISSN 0001-4966.
- ^ Roche (2004, 'String gauges and altered tunings', p. 169–170)
- ^ Bowcott, Nick (10 September 2008). "The Doom Generation: The Art of Playing Heavy". Guitar World. Retrieved 28 March 2019.
- ^ Long, Ben. "Drop D Tuning". Archived from the original on 10 November 2017.
- ^ Tolinski, Brad (September 1994). "Heavy Mental – Interview". Blue Cricket Media.
- ^ a b Sethares (2009, p. 16)
- ^ a b Denyer (1992, p. 158)
- ^ Denyer (1992, p. 160)
- ^ Gold, Jude (December 2005). "Just desserts: Steve Kimock shares the sweet sounds of justly tuned thirds and sevenths". Master class. Guitar Player.[dead link]
- ^ a b Annala & Mätlik (2007, p. 30)
- ^ Ophee, Matanya (ed.). 19th Century etudes for the Russian 7-string guitar in G Op. The Russian Collection. Vol. 9. Editions Orphee. PR.494028230. Archived from the original on 4 July 2013.
– Ophee, Matanya (ed.). Selected Concert Works for the Russian 7-String Guitar in G open tuning. The Russian Collection. Vol. 10. Editions Orphee. PR.494028240. Archived from the original on 4 July 2013. - ^ a b Timofeyev, Oleg V. (1999). The golden age of the Russian guitar: Repertoire, performance practice, and social function of the Russian seven-string guitar music, 1800–1850. Duke University, Department of Music. pp. 1–584. University Microfilms (UMI), Ann Arbor, Michigan, number 9928880.
- ^ Grossman (1972, p. 29)
- ^ Sethares (2009, pp. 20–21)
- ^ Sethares (2009, pp. 18–19)
- ^ Baughman, Steve (2004). "Open C". Mel Bay Beginning Open Tunings. Pacific, Missouri: Mel Bay Publications. pp. 8–14. ISBN 978-0-7866-7093-2.
- ^ Guitar Tunings Database (2013). "CCGCEG Guitar Tuner". CCGCEG: Open C via harmonic overtones. Archived from the original on 10 March 2013. Retrieved 20 February 2013.
- ^ Persichetti (1961, pp. 23–24)
- ^ a b Sharken, Lisa (15 May 2001). "Mick Ralphs: The rock 'N' roll fantasy continues". Vintage Guitar. Archived from the original on 8 February 2013. Retrieved 21 February 2013.
- ^ "List of all Guitar and Piano Transcriptions". GGDGBD. JoniMitchell.com. Archived from the original on 18 May 2015. Retrieved 22 February 2013.
- ^ Ellis, Andy (2005). "How to play like ... Keith Richards". Guitar Player. Retrieved 24 March 2013.[dead link]
- ^ Bellow (1970, p. 164)
- ^ "Piano Chord Chart". 8notes.com. Archived from the original on 14 June 2017. Retrieved 6 May 2018.
- ^ Sethares (2001, p. 16)
- ^ Cohen, Andy (22 March 2005). "Stefan Grossman- Country Blues Guitar in Open Tunings". Sing Out!. 49 (1): 152.
- ^ Starlin, Mark (5 May 2007). "Better Guitar - Article on Tuning Down A Half Step". Archived from the original on 5 May 2007. Retrieved 9 September 2023.
- ^ Serna, Desi (2015). Guitar Rhythm and Technique For Dummies. For Dummies. p. 80. ISBN 978-1-119-02287-9. Retrieved 25 January 2019.
it's fairly common in rock music for guitarists to tune all of their strings down by a half-step
- ^ Denyer (1992, p. 119)
- ^ Sethares (2001, p. 52)
- ^ a b Kirkeby, Ole (1 March 2012). "Major thirds tuning". m3guitar.com. cited by Sethares (2011). Archived from the original on 11 April 2015. Retrieved 10 June 2012.
- ^ White, Mark (Fall 2005). "Reading skills: The guitarist's nemesis?". Berklee Today. Vol. 17, no. 2. Boston, MA: Berklee College of Music. ISSN 1052-3839.
- ^ Denyer (1992, p. 72)
- ^ Peterson (2002, p. 37)
- ^ Griewank (2010, p. 5)
- ^ Sethares (2001, pp. 54–55)
- ^ Sethares (2001, pp. 58–59)
- ^ Bianco, Bob (1987). Guitar in Fourths. New York City: Calliope Music. ISBN 0-9605912-2-2. OCLC 16526869.
- ^ Ferguson (1986, p. 76)
- ^ a b Sethares (2001, pp. 56)
- ^ a b c Peterson (2002, pp. 36–37)
- ^ a b Griewank (2010)
- ^ a b c Patt, Ralph (14 April 2008). "The major 3rd tuning". Ralph Patt's jazz web page. ralphpatt.com. cited by Sethares (2011). Retrieved 10 June 2012.
- ^ Griewank (2010, p. 9)
- ^ Griewank (2010, p. 2)
- ^ Griewank (2010, p. 10)
- ^ Denyer (1992, p. 121)
- ^ Sethares (2001, 'The mandoguitar tuning' 62–63)
- ^ Mulhern, Tom (January 1986). "On the discipline of craft and art: An interview with Robert Fripp". Guitar Player. 20: 88–103. Archived from the original on 16 February 2015. Retrieved 8 January 2013.
- ^ Tamm (2003)
- ^ Sethares (2001, 'The mandoguitar tuning', pp. 62–63)
- ^ Whitehill, Dave; Alternate Tunings for Guitar; p. 5 ISBN 0793582199
References
- Allen, Warren (22 September 2011) [30 December 1997]. "WA's encyclopedia of guitar tunings". Archived from the original on 13 July 2012. Retrieved 27 June 2012. (Recommended by Marcus, Gary (2012). Guitar zero: The science of learning to be musical. Oneworld. p. 234. ISBN 978-1-85168-932-3.)
- Annala, Hannu; Mätlik, Heiki (2007). "Composers for other plucked instruments: Rudolf Straube (1717–1785)". Handbook of Guitar and Lute Composers. Translated by Katarina Backman. Mel Bay. ISBN 978-0-7866-5844-2.
- Bellow, Alexander (1970). The illustrated history of the guitar. Colombo Publications.
- Denyer, Ralph (1992). "Playing the guitar ('How the guitar is tuned', pp. 68–69, and 'Alternative tunings', pp. 158–159)". The guitar handbook. Special contributors Isaac Guillory and Alastair M. Crawford (Fully revised and updated ed.). London and Sydney: Pan Books. pp. 65–160. ISBN 0-330-32750-X.
- Ferguson, Jim (1986). "Stanley Jordan". In Casabona, Helen; Belew, Adrian (eds.). New directions in modern guitar. Guitar Player basic library. Hal Leonard Publishing. pp. 68–76. ISBN 978-0-88188-423-4.
- Griewank, Andreas (1 January 2010), Tuning guitars and reading music in major thirds, Matheon preprints, vol. 695, Berlin, Germany: DFG research center "MATHEON, Mathematics for key technologies" Berlin, urn:nbn:de:0296-matheon-6755. Postscript file and Pdf file, archived from the original on 8 November 2012
- Grossman, Stefan (1972). The book of guitar tunings. New York: Amsco Publishing Company. ISBN 0-8256-2806-7. LCCN 74-170019.
- Persichetti, Vincent (1961). Twentieth-century harmony: Creative aspects and practice. New York: W. W. Norton. ISBN 0-393-09539-8. OCLC 398434.
- Peterson, Jonathon (2002). "Tuning in thirds: A new approach to playing leads to a new kind of guitar". American Lutherie: The Quarterly Journal of the Guild of American Luthiers. 72 (Winter). Tacoma, WA: The Guild of American Luthiers: 36–43. ISSN 1041-7176. Archived from the original on 21 October 2011. Retrieved 9 October 2012.
- Roche, Eric (2004). "5 Thinking outside the box". The acoustic guitar Bible. London: Bobcat Books Limited, SMT. pp. 151–178. ISBN 1-84492-063-1.
- Sethares, Bill (2001). "Regular tunings" (PDF). Alternate tuning guide. Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 52–67. Retrieved 19 May 2012.
- Sethares, Bill (2009) [2001]. Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012.
- Sethares, William A. (2011). "Alternate tuning guide". Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012.
- Tamm, Eric (2003) [1990]. "Chapter Ten: Guitar Craft". Robert Fripp: From crimson king to crafty master. Faber and Faber. ISBN 0-571-16289-4. Archived from the original on 26 October 2011. Retrieved 25 March 2012 – via Progressive Ears. Zipped Microsoft Word Document
- Weissman, Dick (2006). Guitar tunings: A comprehensive guide. Routledge. ISBN 978-0-415-97441-7. LCCN 0415974410.[permanent dead link]
Further reading
- Anonymous (2000). Alternate tunings guitar essentials. Acoustic Guitar Magazine's private lessons. String Letter Publishing. Hal Leonard Publishing Corporation. ISBN 978-1-890490-24-9. LCCN 2001547503.
- Hanson, Mark (1995). The complete book of alternate tunings. Accent on Music. ISBN 978-0-936799-13-1.
- Hanson, Mark (1997). Alternate tunings picture chords. Accent on Music. ISBN 978-0-936799-14-8.
- Heines, Danny (2007). Mastering alternate tunings: A revolutionary system of fretboard navigation for fingerstyle guitarists. Hal Leonard. ISBN 978-0-634-06569-9.
- Johnson, Chad (2002). Alternate tuning chord dictionary. Hal Leonard. ISBN 978-0-634-03857-0. LCCN 2005561612.
- Maloof, Richard (2007). Alternate tunings for guitar. Cherry Lane Music Company. ISBN 978-1-57560-578-4. LCCN 2008560110.
- Shark, Mark (2008). The tao of tunings: A map to the world of alternate tunings. Hal Leonard Corporation. ISBN 978-1-4234-3087-2.
External links
- Allen, Warren (22 September 2011) [30 December 1997]. "WA's Encyclopedia of Guitar Tunings". Retrieved 27 June 2012. (Recommended by Marcus, Gary (2012). Guitar zero: The science of learning to be musical. Oneworld. p. 234. ISBN 978-1-85168-932-3.)
- Sethares, William A. (12 May 2012). "Alternate tuning guide: Interactive". Uses Wolfram Cdf player. Retrieved 27 June 2012.