Grötzsch graph
| Grötzsch graph | |
|---|---|
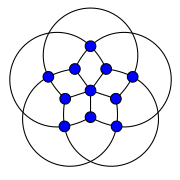 | |
| Named after | Herbert Grötzsch |
| Vertices | 11 |
| Edges | 20 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 10 (D5) |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.[1]
The Grötzsch graph is a member of an infinite sequence of triangle-free graphs, each the Mycielskian of the previous graph in the sequence, starting from the one-edge graph; this sequence of graphs was constructed by Mycielski (1955) to show that there exist triangle-free graphs with arbitrarily large chromatic number. Therefore, the Grötzsch graph is sometimes also called the Mycielski graph or the Mycielski–Grötzsch graph. Unlike later graphs in this sequence, the Grötzsch graph is the smallest triangle-free graph with its chromatic number.[2]
Properties
The full automorphism group of the Grötzsch graph is isomorphic to the dihedral group D5 of order 10, the group of symmetries of a regular pentagon, including both rotations and reflections.[3] These symmetries have three orbits of vertices: the degree-5 vertex (by itself), its five neighbors, and its five non-neighbors. Similarly, there are three orbits of edges, distinguished by their distance from the degree-5 vertex.
The characteristic polynomial of the Grötzsch graph is[3]
Although it is not a planar graph, it can be embedded in the projective plane without crossings. This embedding has ten faces, all of which are quadrilaterals.[4]
Applications
The existence of the Grötzsch graph demonstrates that the assumption of planarity is necessary in Grötzsch's theorem that every triangle-free planar graph is 3-colorable.[1] It has odd girth five but girth four, and does not have any graph homomorphism to a graph whose girth is five or more, so it forms an example that distinguishes odd girth from the maximum girth that can be obtained from a homomorphism.[5]
Häggkvist (1981) used a modified version of the Grötzsch graph to disprove a conjecture of Paul Erdős and Miklos Simonovits (1973) on the chromatic number of triangle-free graphs with high degree. Häggkvist's modification consists of replacing each of the five degree-four vertices of the Grötzsch graph by a set of three vertices, replacing each of the five degree-three vertices of the Grötzsch graph by a set of two vertices, and replacing the remaining degree-five vertex of the Grötzsch graph by a set of four vertices. Two vertices in this expanded graph are connected by an edge if they correspond to vertices connected by an edge in the Grötzsch graph. The result of Häggkvist's construction is a 10-regular triangle-free graph with 29 vertices and chromatic number 4, disproving the conjecture that there is no 4-chromatic triangle-free -vertex graph in which each vertex has more than neighbours.[6] Every such graph contains the Grötzsch graph as an induced subgraph.[7]
Related graphs
The Grötzsch graph shares several properties with the Clebsch graph, a distance-transitive graph with 16 vertices and 40 edges: both the Grötzsch graph and the Clebsch graph are triangle-free and four-chromatic, and neither of them has any six-vertex induced paths. These properties are close to being enough to characterize these graphs: the Grötzsch graph is an induced subgraph of the Clebsch graph, and every triangle-free four-chromatic -free graph is likewise an induced subgraph of the Clebsch graph that in turn contains the Grötzsch graph as an induced subgraph.[8] The Chvátal graph is another small triangle-free 4-chromatic graph. However, unlike the Grötzsch graph and the Clebsch graph, the Chvátal graph has a six-vertex induced path.
Notes
References
- Brandt, Stephan (1999), "On the structure of dense triangle-free graphs", Combinatorics, Probability and Computing, 8 (3): 237–245, doi:10.1017/S0963548399003831, MR 1702550, S2CID 120967754
- Chvátal, Vašek (1974), "The minimality of the Mycielski graph", Graphs and combinatorics (Proc. Capital Conf., George Washington Univ., Washington, D.C., 1973), Berlin: Lecture Notes in Mathematics, Vol. 406, Springer-Verlag, pp. 243–246, MR 0360330
- Erdős, P.; Simonovits, M. (1973), "On a valence problem in extremal graph theory", Discrete Mathematics, 5 (4): 323–334, doi:10.1016/0012-365X(73)90126-X, MR 0342429
- Galluccio, Anna; Goddyn, Luis A.; Hell, Pavol (2001), "High-girth graphs avoiding a minor are nearly bipartite", Journal of Combinatorial Theory, Series B, 83 (1): 1–14, doi:10.1006/jctb.2000.2009, MR 1855793
- Grötzsch, Herbert (1959), "Zur Theorie der diskreten Gebilde, VII: Ein Dreifarbensatz für dreikreisfreie Netze auf der Kugel", Wiss. Z. Martin-Luther-U., Halle-Wittenberg, Math.-Nat. Reihe, 8: 109–120, MR 0116320
- Häggkvist, R. (1981), "Odd cycles of specified length in nonbipartite graphs", Graph Theory (Cambridge, 1981), pp. 89–99, MR 0671908
- Joyner, W. David; Melles, Caroline Grant (2017), "5.12 Grötzsch graph", Adventures in Graph Theory, Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, Cham, pp. 229–231, doi:10.1007/978-3-319-68383-6, ISBN 978-3-319-68381-2, MR 3753658
- Mycielski, Jan (1955), "Sur le coloriage des graphs", Colloq. Math., 3 (2): 161–162, doi:10.4064/cm-3-2-161-162, MR 0069494
- Randerath, Bert; Schiermeyer, Ingo; Tewes, Meike (2002), "Three-colourability and forbidden subgraphs. II. Polynomial algorithms", Discrete Mathematics, 251 (1–3): 137–153, doi:10.1016/S0012-365X(01)00335-1, MR 1904597
- Youngs, D. A. (1996), "4-chromatic projective graphs", Journal of Graph Theory, 21 (2): 219–227, doi:10.1002/(SICI)1097-0118(199602)21:2<219::AID-JGT12>3.0.CO;2-E, MR 1368748



