Newton line
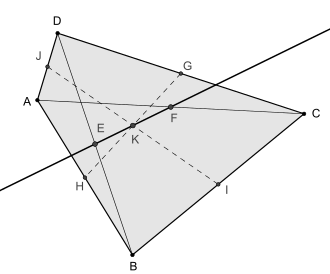
In Euclidean geometry the Newton line is the line that connects the midpoints of the two diagonals in a convex quadrilateral with at most two parallel sides.[1]
Properties
The line segments GH and IJ that connect the midpoints of opposite sides (the bimedians) of a convex quadrilateral intersect in a point that lies on the Newton line. This point K bisects the line segment EF that connects the diagonal midpoints.[1]
By Anne's theorem and its converse, any interior point P on the Newton line of a quadrilateral ABCD has the property that
where [△ABP] denotes the area of triangle △ABP.[2]
If the quadrilateral is a tangential quadrilateral, then its incenter also lies on this line.[3]
See also
References
- ^ a b Alsina, Claudi; Nelsen, Roger B. (2010). Charming Proofs: A Journey Into Elegant Mathematics. Mathematics Association of America. pp. 108–109. ISBN 9780883853481.
- ^ Alsina & Nelsen (2010), pp. 116–117.
- ^ Djukić, Dušan; Janković, Vladimir; Matić, Ivan; Petrović, Nikola (2006). The IMO Compendium: A Collection of Problems Suggested for The International Mathematical Olympiads: 1959-2004. Problem Books in Mathematics. Springer. p. 15. doi:10.1007/0-387-33430-0. ISBN 0-387-24299-6.
External links
- Weisstein, Eric W. "Léon Anne's Theorem". MathWorld.
- Alexander Bogomolny: Bimedians in a Quadrilateral at cut-the-knot.org
![{\displaystyle [\triangle ABP]+[\triangle CDP]=[\triangle ADP]+[\triangle BCP],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab69931aa3134a0fab625b8bb56e61978926d8b)