Ĵongla notacio

Ĵongla skribsistemo (angle siteswap = lokŝanĝado) estas skribsistemo (aŭ notacio) kiu priskribas la ritmon de la ĵetoj kaj do la objektaj vojoj por la ĵonglado, simile al muzika skribsistemo por la muzikistoj. Ĝi iĝis modelo por priskribi kaj komuniki la ĵongladaj movaroj sole kaj inter pluraj ĵonglistoj. La skribsistemo estas sekvo de ciferoj signifanta por ĉiu ĵeto la nombro de tempoj ĝis la sekva samobjekta ĵeto. Tio permesas modeligi kaj inventi senfinajn sekvaĵojn, por iom ajn objektoj kaj ĵetlokoj (ekzemple la nombro de manoj). Samtempe simpla kaj potencega, la ĵonglskribsistemo multe partoprenis en plivastigo de la ĵonglaj movaĵaj eblecoj.
La ĵonglskribo ĉefe taŭgas por la aera ĵonglado (pilkoj, klaboj, ringoj...). Tamen, eblas ankaŭ uzi ĝin por resalta ĵonglado kaj eĉ por la diabolo.
Historio
La plej simpla sistemo (kelkfoje nomata angle vanilla siteswap) priskribas alitempan ĵongladon per du manoj. Ĝi estis farata de tri sendependaj aroj dum la jaro 1980: Paul Klimek en Santa Cruz kaj Bruce Tiemann ĉe la Kalifornia Instituto de Teknologio en Kalifornio; Mike Day, Colin Wright kaj Adam Chalcraft en Kembriĝo.
La dissendolisto rec.juggling funkciante ekde aŭgusto 1990 ĉe Uzreto[1] kaj la komenco de interreto permesis rapidan diskonigon de tiuj ideoj inter la ĵonglantaj sciencistoj. Rec.juggling ankoraŭ estas nun la plej plena informfonto pri la siteswap.
Kelkaj ĵonglrenkontiĝoj poste permesis adaptiĝon por la interdonado, la ĵongla tipo (alitempa aŭ samtempa) kaj la ĵetspecoj.
En 1991 la plurmana sistemo de Ed Cartsen (multihand notation) resumas plejparton el konataj nocioj. Ĝi permesas priskribi ankaŭ la alitempecon per samaj skriboj kiel samtempecon, por kiom ajn ĵetlokoj. Ĝi utilis ekzemple ekde la dekjarfino 1990 al la aro Gandini Juggling por realigi ĵonglskribajn sekvojn interdonadaj per nepara nombro de manoj, aŭ ĉirkaŭ 2002 al diabolistoj kies ŝnureto povas esti rigardata kiel ĵetloko. En 2005, la plurmana sistemo estas plue sufiĉa por priskribi la tipo plurritma.
Bazoj: ĵonglskriboj alitempaj

La plej baza speco de ĵonglskribsistemo priskribas la sekvojn kie la ĵetoj estas alitempaj (alternas inter la dekstra kaj maldekstra mano) kaj kie nur unu pilko estas ĵetata samtempe. Se oni filmus dealte ĵongliston ĵetantan ĉiun pilkon alterne inter la du manoj, kaj antaŭirantan, oni vidus io kio similus al dekstra bildo, kelkfoje nomata spacatempa diagramo, komparebla kun ĝia samaĵo en fiziko.
Por priskribi la sekvon, oni sciigas kiom da tempo poste la objekto estos reĵetata. Ekzemple, se oni rigardas la dekstran diagramon, je la unua ĵeto, la violkolora pilko estas ĵetata per la dekstra mano, poste la blua, poste la verda, ree la verda, ree la blua kaj finfine la viola estas kaptata kaj reĵetata per la maldekstra mano dum la kvina tempo: Tio donas al la unua ĵeto la valoron 5. Refarante tiel por ĉiuj tempoj, oni ekhavas sekvon de ciferoj kiuj signifas, por ĉiu ĵeto, la tempon ĝis la venonta reĵeto. Pro tio ke la ĵetoj alternas de unu mano al la alia, la neparaj ciferoj signifas ke oni ĵetas la pilkon el iu mano al la alia (kruca ĵeto), dum la paraj ciferoj signifas ke la pilko estas kaptata per la sama mano kiu ĵetis ĝin (nekruca ĵeto).
Ciferoj
Pro tio ke la cifero priskribanta ĵeton regas le tempon ĝis la sekva ĵeto, ĝi ankaŭ povas esti rigardata kiel la alteco de la ĵeto. Tial, plejofte oni rigardas la ciferojn kiel la alteco de la ĵetoj:
- 3 signifas ĵeton tiel altan, kiel oni ĵetas kiam oni ĵonglas per 3 pilkoj (kruca);
- 4 signifas ĵeton tiel altan, kiel oni ĵetas kiam oni ĵonglas per 4 pilkoj (nekruca);
- 5 signifas ĵeton tiel altan, kiel oni ĵetas kiam oni ĵonglas per 5 pilkoj (kruca);
- ...
- A signifas ĵeton tiel altan, kiel oni ĵetas kiam oni ĵonglas per 10 pilkoj (nekruca);
- B signifas ĵeton tiel altan, kiel oni ĵetas kiam oni ĵonglas per 11 pilkoj (kruca);
- kaj tiel plu.
Kvankam neĝusta, tio tre utilas dum praktiko ĉar tio permesas fari rekte la sekvon sen bezoni pensi pri ĉiuj interŝanĝoj. Tio priskribas nur relativan altecon, ĉar tiu ĉi dependas de la ritmo, kaj aliaj.
Estas tri apartaj ciferoj:
- 0 signifas ke dum unu tempo la mano estas malplena;
- 1 priskribas rekta ĵeto aŭ dono manalmane;
- 2 signifas ke, dum unu tempo, la objekto restas en la mano. Tamen eblas anstataŭi tion per nekruca ĵeto.
Akordiĝe, oni skribas la siteswap komence per la plej grandaj ciferoj. Tiel la samaj siteswap 315, 153 kaj 531 estas ĉiuj skribataj 531.
Simetrieco
Ĉiu sekvo ripetiĝas post iom da ĵetoj: tio estas la periodo. La sekvo estas do skribata per la plej eta ero: la dekstra sekvo estas tiel skribata 53 145 305 520, kaj ties periodo estas 11. Kiam la periodo estas nepara (kiel tiu ekzemplo), la sekvo estas simetria ĉar la ripeto komencos per la alia mano. Ĉiuj ĵetoj estas farataj alterne per ĉiu mano. La sekvoj kun para periodo estas nesimetriaj: ĉiu mano ripetas ĉiam la samajn ĵetojn.
Nombro de ĵongliloj
La nombro de ĵongliloj bezonataj por ĵongli la sekvon estas la aritmetika meznombro. Tiel, 441 estas ĵonglata per 3 objektoj, ĉar (4+4+1)/3 = 3, 86 per 7 objektoj, 7531 per 4, ktp. Ĉiu valida sekvo havas do aritmetikan meznombron plenan, sed tio ne estas sufiĉa kondiĉo. Ekzemple, la sekvo 543 ne validas, ĉar ĉiuj pilkoj devas esti reĵetitaj samtempe. Ĉiu valida sekvo kies aritmetika meznombro estas plena povas esti enordigi al valida sekvo laŭ la enordiga teoremo[2].
Ĵonglskriboj samtempaj
La baza ĵonglskribsistemo (vanilla) priskribas nur la movojn alitempajn: la du manoj ĵetas alterne objektojn. Ĉiu mano ĵetas ĉiun duan tempon. Sed la ĵonglado ankaŭ eblas per malpli multaj movaĵoj samtempaj, la du manoj ĵetas samtempe. Tiel, ĉar estas du ĵetoj dum la sama tempo, oni skribas la du ĵetoj inter rondaj krampoj, kun komo inter ili: ekzemple (4,4). En samtempaj ĵonglskriboj, kiel en alitempa, ĉiu mano ĵetas duontempe.
La regulo pri la aritmetika meznombro estas ĉiam valida: ekzemple por (4,4) bezonas (4 + 4) / 2 = 4 objektojn).
Kiam la ĵeto estas kruca, oni aldoas ikson post la cifero. Ekzemple, (4,2x)(2x, 4) estas la skatolo per tiuj objektoj, figurata per la dekstra diagramo.
Samtempa ĵonglskribo povas havi steleton fine. Tiu signifas ke la sekvo devas esti reĵonglata dekomence alterne per la du manoj: la sekvo estas simetria. Tiel, (4,2x)(2x,4) mallongeblas per (4,2x)*, kaj (6x, 4)(4,2x)* signifas (6x,4)(4,2x)(4,6x)(2x,4).
Ecoj
Ĵonglskriba sekvo povas esti:
- fundamenta kiam ĝi rekte fareblas ekde la baza stato (do, kiam oni povas fari ĝin tuj kaj sen transiro ekde akvofalo aŭ akvofonto laŭ la pareco). 441 estas fundamenta sekvo: oni rekte povas ĵongli 441 post akvofalo 3, kaj poste ankoraŭ rekte ree 3. Ĉiuj fundamentaj sekvoj por iu nombro de objekto sekveblas sentransire: 531, 441 kaj 423 ĵongleblas per iu ajn ordo, ekzemple 531 531 441 423 423.
- ekscitata kiam ĝi estas ne fundamenta, tio estas kiam ĝi ne rekte fareblas ekde la baza stato. Ĝi bezonas transiron por eniri kaj foriri. Triobjekta duŝo 51 estas ekscitata sekvo, ĉar ne eblas sekvigi 3 kaj 51, bezonas transiron, ekzemple: 3 (4) 51 (2) 3. Tansiroj ofte estas skribataj inter rondkrampoj.
- unua kiam ĝi ne eriĝeblas en pluraj sekvoj sendependaj. Alie, oni povas diri ke ĝi neniam iras per la sama stato. Tiel 3, 441 kaj 633 estas sekvoj unuaj dum 423 ne estas unua ĉar ĝi eriĝeblas en 42 kaj 3. Unua sekvo povas esti aŭ ekscitata (ekzemple 51, 741) aŭ fundamenta (ekzemple 642, 97 531).
Plurobjektaj ĵetoj
Plurobjektaj ĵetoj (angle multiplex) estas ĵeto samtempa de pluraj objektoj per la sama mano. La vastiĝa skribsistemo siteswap uzas rekntaj krampojn por priskribi tiujn ĵetojn. Ekzemple [54] signifas ke la mano ĵetas samtempe du objektojn : unu kiel 5 kaj la alia kiel 4.
La nombro de ciferoj ĉeestantaj inter la rektkrampoj estas la nombro de objektoj bezonataj por ĵongli la plurobjekta ĵeto:
- [54] estas duobjekta ĵeto,
- [432] estas triobjekta ĵeto,
- [6543] estas kvarobjekta ĵeto,
- [97 531] estas kvinobjekta ĵeto...
Laŭ kutimoj kaj programoj, la ĵetoj inter rektkrampoj estas enordigi aŭ kreske aŭ malkreske. Por distingi apartigi tiujn ĵetojn elparole, oni ĝenerale elparolas ilin kiel nombroj kaj ne ciferoj. Ekzemple [43]23 estas alparolata: kvardek tri - du - tri.
Brakaj movaĵoj
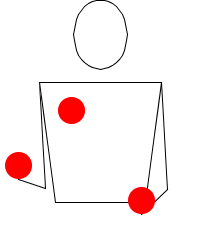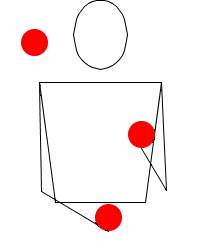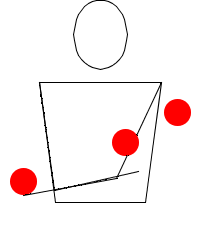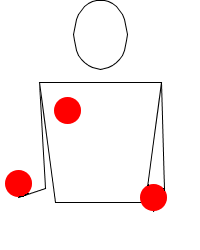
Ankaŭ eblas priskribi per ĵonglskribsistemo la brakmovojn, por movoj kiel Mills senordo kaj aliaj.
Referencoj
- ↑ angle statistikoj pri rec.juggling Arkivigite je 2007-04-30 per la retarkivo Wayback Machine
- ↑ Benoît Guerville, Théorème de réorganisation, januaro 2009.
Eksteraj ligiloj
- Artikoloj pri ĵonglskribsistemo Arkivigite je 2011-01-07 per la retarkivo Wayback Machine (siteswap) (katalune, dane, germane, greke, angle, hispane, france, hebree, itale, japane, nederlande, ruse)
- Juggling Lab animator Programo por ĵonglskribsistemo