Grupo espacial
En matemáticas y física, un grupo espacial es el grupo simétrico de una configuración en el espacio, generalmente en tres dimensiones. En tres dimensiones, existen 219 tipos distintos, o bien 230 si se consideran distintas las copias quirales. Los grupos espaciales estudiados en más de 3 dimensiones se denominan Grupos de Bieberbach, (por Ludwig Bieberbach) y son grupos discretos compactos de isometrías de un espacio euclídeo orientado. En cristalografía, los grupos espaciales también se suelen denominar grupos de Fedorov o cristalográficos, y representan la descripción de la simetría del cristal. Una fuente bibliográfica representativa de los grupos espaciales tridimensionales es el International Tables for Crystallography (Hann (2002)).
Historia
Los grupos espaciales en 2 dimensiones son 17 grupos de simetría plana los cuales se conocen desde hace siglos aunque la prueba de que la lista estaba completa no se dio hasta 1891, después de que se hubieran considerado casos más complejos de grupos espaciales.
En 1879 Leonhard Sohncke enumeró los 65 grupos espaciales (en ocasiones llamados Grupos espaciales de Sohncke o Grupos espaciales quirales) cuyos elementos preservaban la orientación. Más detalladamente, listó 66 grupos, pero Yevgraf Stepánovich Fiódorov y Arthur Moritz Schönflies advirtieron que en realidad dos de ellos eran el mismo. Los grupos espaciales en 3 dimensiones fueron enumerados por primera vez por Fiódorov (1891) (cuya lista tenía dos omisiones (I43d y Fdd2) y una duplicación (Fmm2)), y poco después fueron enumerados de forma independiente por Schönflies (1891) (cuya lista tenía cuatro omisiones (I43d, Pc, Cc, ?) y una duplicación (P421m)). La lista correcta de los 230 grupos espaciales fue descubierta en 1892 durante la correspondencia entre Fiódorov y Schönflies. Más tarde William Barlow (1894) enumeró los grupos con un método diferente, pero omitió cuatro grupos (Fdd2, I42d, P421d, yP421c) incluso cuando ya tenía la lista correcta de los 230 grupos creada por Fiódorov y Schönflies.
Burckhardt (1967) describe en detalle la historia del descubrimiento de los grupos espaciales.
Elementos de un grupo espacial
Los grupos espaciales en tres dimensiones están formados por combinaciones de los 32 grupos de puntos cristalográficos con las 14 redes de Bravais, y cada una de estas pertenece a uno de los 7 sistemas de redes. Este resultado exprime que cada grupo espacial es una combinación de la simetría de traslación de una celda unitaria incluyendo el centro de redes, las operaciones de simetría del grupo de puntos de reflexión, rotación y/o rotación impropia (también llamada rotoreflexión), y el eje helicoidal y el plano de deslizamiento de operaciones simétricas. La combinación de todas estas operaciones de simetría dan lugar a un total de 230 grupos espaciales diferentes que describen todas las posibles simetrías cristalinas.
Elementos de fijación de un punto
Los elementos de los grupos espaciales que permiten fijar un punto del espacio son rotaciones, reflexiones, el elemento de identidad y la rotación impropia
Traslaciones
Las traslaciones forman un subgrupo abeliano normal de rango 3, llamado red de Bravais. Hay 14 posibles tipos de redes de Bravais. El cociente entre grupos espaciales y la red de Bravais da como resultado un grupo finito que será uno de los 32 posibles grupos puntuales. La traslación se define como el movimiento de un punto de un lado a otro de la cara.
Planos de deslizamiento
Un plano de deslizamiento es una reflexión en un plano, seguida por una traslación paralela con ese mismo plano. Se denota a, b,c, dependiendo del eje de deslizamiento sobre el que se produce. Existe también el deslizamiento n, que es un deslizamiento a lo largo de la mitad de la diagonal de una cara; y el deslizamiento d, que es un deslizamiento a lo largo de un cuarto del camino de cualquier cara o espacio diagonal de una celda unitaria. Se conoce también como plano de deslizamiento del diamante al aparecer en la estructura del diamante.
Ejes helicoidales
Un eje helicoidal es una rotación sobre un eje, seguida de una traslación a lo largo de la dirección del eje. Se denotan con un número, n, que describe el grado de rotación ya que es el número de operaciones que se necesita aplicar para obtener una rotación total. El grado de traslación se añade como subíndice mostrando cuán lejos en el eje se produce la traslación, como una porción del vector de red paralelo. Por ejemplo, 21 es una rotación doble seguida de una traslación de ½ del vector de red.
Fórmula general
La fórmula general para la acción de un elemento de un grupo espacial es y = M • x + D donde M es la matriz, D es el vector, y las transformaciones elementales transforman el punto x en el punto y. En general, D = D(red) + D(M), donde D(M) es una función única de M que se hace cero cuando M es la identidad. Las matrices M forman un grupo puntual que es la base del grupo espacial; la red debe ser simétrica bajo ese grupo puntual.
La dimensión de la red puede ser menor que la dimensión total, dando lugar a un grupo espacial “subperiódico”. Para (dimensión total, dimensión de la red):
- (1,1): grupo lineal unidimensional
- (2,1): grupo lineal bidimensional: frisos
- (2,2): grupo de simetría plana
- (3,1): grupo lineal tridimensional; con los grupos puntuales cristalográficos en 3D
- (3,2): grupo capa
- (3,3): grupos espaciales (los discutidos en este artículo)
Tabla de grupos espaciales en 2 dimensiones (simetría plana)
Tabla de la simetría plana utilizando la clasificación de grupos espaciales tridimensionales:
| Sistema cristalino (Red de Bravais) |
Clasificación geométrica Grupo puntual |
Clasificación aritmética |
Grupos de simetría plana (diagrama de celda) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Schön. | Notación Orbifold | Cox. | Ord. | ||||||
| Oblicuo |
C1 | (1) | [ ]+ | 1 | Ninguna | p1 (1) |
|||
| C2 | (22) | [2]+ | 2 | Ninguna | p2 (2222) |
||||
Rectangular
|
D1 | (*) | [ ] | 2 | Lineal | pm (**) |
pg (××) |
||
| D2 | (*22) | [2] | 4 | Lineal | pmm (*2222) |
pmg (22*) |
|||
| Rectangular (Rombo) 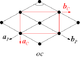
|
D1 | (*) | [ ] | 2 | Intervalo | cm (*×) |
|||
| D2 | (*22) | [2] | 4 | Intervalo | cmm (2*22) |
pgg (22×) |
|||
Cuadrado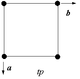
|
C4 | (44) | [4]+ | 4 | Ninguna | p4 (442) |

|
||
| D4 | (*44) | [4] | 8 | Ambas | p4m (*442) |

|
p4g (4*2) |

| |
Hexagonal
|
C3 | (33) | [3]+ | 3 | Ninguna | p3 (333) |
|||
| D3 | (*33) | [3] | 6 | Intervalo | p3m1 (*333) |
p31m (3*3) |
|||
| C6 | (66) | [6]+ | 6 | Ninguna | p6 (632) |
||||
| D6 | (*66) | [6] | 12 | Ambos | p6m (*632) |
||||
Para cada clasificación geométrica, las posibles clases aritméticas son:
- Ninguna: no hay líneas de reflexión
- Linear: las líneas de reflexión van a lo largo de las direcciones de la red
- Intervalo: la mitad de las líneas de reflexión están comprendidas en las direcciones de red
- Ambas: se dan las dos anteriores
Tabla de grupos espaciales en 3 dimensiones
| # | Sistema cristalino red de Bravais |
Grupo puntual | Grupos espaciales (Abreviatura internacional) | ||||
|---|---|---|---|---|---|---|---|
| Intl | Schön. | Notación Orbifold | Cox. | Ord. | |||
| 1 | Triclínico (2) 
|
1 | C1 | 11 | [ ]+ | 1 | P1 |
| 2 | 1 | Ci | 1× | [2+,2+] | 2 | P1 | |
| 3–5 | Monoclínico (13) |
2 | C2 | 22 | [2]+ | 2 | P2, P21 C2 |
| 6–9 | m | Cs | *11 | [ ] | 2 | Pm, Pc Cm, Cc | |
| 10–15 | 2/m | C2h | 2* | [2,2+] | 4 | P2/m, P21/m C2/m, P2/c, P21/c C2/c | |
| 16–24 | Ortorrómbico (59) |
222 | D2 | 222 | [2,2]+ | 4 | P222, P2221, P21212, P212121, C2221, C222, F222, I222, I212121 |
| 25–46 | mm² | C2v | *22 | [2] | 4 | Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2 Cmm2, Cmc21, Ccc2, Amm2, Aem2, Ama2, Aea2 Fmm2, Fdd2 Imm2, Iba2, Ima2 | |
| 47–74 | mmm | D2h | *222 | [2,2] | 8 | Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce Fmmm, Fddd Immm, Ibam, Ibca, Imma | |
| 75–80 | Tetragonal (68) |
4 | C4 | 44 | [4]+ | 4 | P4, P41, P42, P43, I4, I41 |
| 81–82 | 4 | S4 | 2× | [2+,4+] | 4 | P4, I4 | |
| 83–88 | 4/m | C4h | 4* | [2,4+] | 8 | P4/m, P42/m, P4/n, P42/n I4/m, I41/a | |
| 89–98 | 422 | D4 | 224 | [2,4]+ | 8 | P422, P4212, P4122, P41212, P4222, P42212, P4322, P43212 I422, I4122 | |
| 99–110 | 4mm | C4v | *44 | [4] | 8 | P4mm, P4bm, P42cm, P42nm, P4cc, P4nc, P42mc, P42bc I4mm, I4cm, I41md, I41cd | |
| 111–122 | 42m | D2d | 2*2 | [2+,4] | 8 | P42m, P42c, P421m, P421c, P4m², P4c2, P4b2, P4n2 I4m², I4c2, I42m, I42d | |
| 123–142 | 4/mmm | D4h | *224 | [2,4] | 16 | P4/mmm, P4/mcc, P4/nbm, P4/nnc, P4/mbm, P4/mnc, P4/nmm, P4/ncc, P42/mmc, P42/mcm, P42/nbc, P42/nnm, P42/mbc, P42/mnm, P42/nmc, P42/ncm I4/mmm, I4/mcm, I41/amd, I41/acd | |
| 143–146 | Trigonal (25)  
|
3 | C3 | 33 | [3]+ | 3 | P3, P31, P32 R3 |
| 147–148 | 3 | S6 | 3× | [2+,6+] | 6 | P3, R3 | |
| 149–155 | 32 | D3 | 223 | [2,3]+ | 6 | P312, P321, P3112, P3121, P3212, P3221 R32 | |
| 156–161 | 3m | C3v | *33 | [3] | 6 | P3m1, P31m, P3c1, P31c R3m, R3c | |
| 162–167 | 3m | D3h | 2*3 | [2+,6] | 12 | P31m, P31c, P3m1, P3c1 R3m, R3c | |
| 168–173 | Hexagonal (27) 
|
6 | C6 | 66 | [6]+ | 6 | P6, P61, P65, P62, P64, P63 |
| 174 | 6 | C3h | 3* | [2,3+] | 6 | P6 | |
| 175–176 | 6/m | C6h | 6* | [2,6+] | 12 | P6/m, P63/m | |
| 177–182 | 622 | D6 | 226 | [2,6]+ | 12 | P622, P6122, P6522, P6222, P6422, P6322 | |
| 183–186 | 6mm | C6v | *66 | [6] | 12 | P6mm, P6cc, P63cm, P63mc | |
| 187–190 | 6m² | D3h | *223 | [2,3] | 12 | P6m², P6c2, P62m, P62c | |
| 191–194 | 6/mmm | D6h | *226 | [2,6] | 24 | P6/mmm, P6/mcc, P63/mcm, P63/mmc | |
| 195–199 | Cúbico (36)   
|
23 | T | 332 | [3,3]+ | 12 | P23, F23, I23 P213, I213 |
| 200–206 | m3 | Th | 3*2 | [3+,4] | 24 | Pm3, Pn3, Fm3, Fd3, Im3, Pa3, Ia3 | |
| 207–214 | 432 | O | 432 | [3,4]+ | 24 | P432, P4232 F432, F4132 I432 P4332, P4132, I4132 | |
| 215–220 | 43m | Td | *332 | [3,3] | 24 | P43m, F43m, I43m P43n, F43c, I43d | |
| 221–230 | m3m | Oh | *432 | [3,4] | 48 | Pm3m, Pn3n, Pm3n, Pn3m Fm3m, Fm3c, Fd3m, Fd3c Im3m, Ia3d | |
Nota. Un plano e es un doble plano de deslizamiento, al tener deslizamientos en dos direcciones diferentes. Se encuentran en siete grupos espaciales ortorrómbicos, grupos espaciales cinco tetragonales y grupos espaciales cinco cúbicos, todos con su centro de red. El uso del símbolo e se hizo oficial con Hahn (2202).
Si el sistema cristalino no es trigonal entonces el sistema de red es del mismo tipo. Si es sistema cristalino sí es trigonal entonces el sistema de red es hexagonal a no ser que el grupo espacial sea uno de los 7 sistemas de red romboédricos consistentes en 7 grupos espaciales trigonales en la tabla superior cuyo nombre comienza con R. El sistema de red hexagonal es mayor que el sistema cristalino hexagonal, y consiste en sistemas cristalinos hexagonales con 18 grupos de sistemas cristalinos trigonales además de los siete cuyo nombre empieza por R.
La red de Bravais de un grupo espacial viene determinada por el sistema de red junto con la letra inicial de su nombre, la cual para los grupos no romboédricos es P, I, F o C que corresponden a principal, centrado en el cuerpo, centrado en la cara, o centrado en la cara C.
Enlaces externos
- Los 17 grupos de simetría, página muy interesante sobre simetrías y teselados