Lemniscata


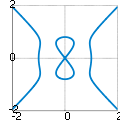
En geometría algebraica, una lemniscata es una cualquiera de varias curvas con figura en forma de ocho (8) o de símbolo de infinito (∞).[1][2]
La palabra proviene del latín "lēmniscātus", que significa "decorado con cintas", a su vez procedente del griego "λημνίσκος" que significa "cintas",[2] que también puede referirse a la forma de la madeja de lana de la que se fabricaban las citadas cintas.[1]
Las curvas generalmente denominadas lemniscata incluyen tres curvas cuárticas: la hipopoda, la lemniscata de Bernoulli, y la lemniscata de Gerono. El estudio de las lemniscatas (y en particular de la hipopoda) se remonta a la matemática helénica, pero el término "lemniscata" para curvas de este tipo proviene del trabajo de Jakob Bernoulli a finales del siglo XVII.
Historia y ejemplos
Lemniscata de Booth
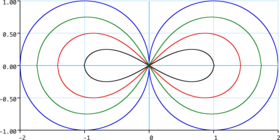
La consideración de las curvas con una figura en forma de ocho se remonta a Proclo, un filósofo y matemático griego del neoplatonismo que vivió en el siglo V d. C. Proclo consideró las secciones de un toro por planos paralelos al eje del toro. Como observó, para la mayoría de las secciones, la sección transversal consiste en uno o dos óvalos; sin embargo, cuando el plano es tangente a la superficie interna del toro, la sección transversal toma una figura con forma de ocho, a la que denominó con la palabra griega hipopoda (por su similitud con la atadura utilizada para inmovilizar dos de las patas de un caballo manteniéndolas juntas). El nombre "lemniscata de Booth" para esta curva se remonta a su estudio por parte del matemático del siglo XIX James Booth.[1]
La lemniscata se puede definir como un curva algebraica, el conjunto de ceros del polinomio cuártico cuando el parámetro d es negativo. Para valores positivos de d se obtiene una hipopoda.
Lemniscata de Bernoulli

En 1680, Cassini estudió una familia de curvas, ahora llamadas óvalos de Cassini, definida de la siguiente manera: el lugar geométrico de todos los puntos tales que el producto de sus distancias respecto a dos puntos fijos, los focos, es una constante. En circunstancias muy particulares (cuando la mitad de la distancia entre los focos es igual a la raíz cuadrada de la constante), esto da lugar a una lemniscata de Bernouilli.
En 1694, Johann Bernoulli estudió el caso de la lemniscata dentro de la familia de los óvalos de Cassini (que pasaría a ser conocida como la lemniscata de Bernoulli mostrado arriba), en relación con un problema de isócronas que había sido planteado anteriormente por Gottfried Leibniz. Al igual que la hipopoda, es una curva algebraica, el conjunto de ceros del polinomio . El hermano de Bernoulli, Jakob Bernoulli, también estudió la misma curva ese mismo año, y le dio su nombre.[3] También se puede definir geométricamente como el lugar de los puntos cuyo producto de distancias desde dos focos es igual al cuadrado de la mitad de la distancia interfocal.[4] Es un caso especial de la hipopoda (lemniscata de Booth), con , y puede formarse como una sección transversal de un toro tal que su orificio interno y sus secciones circulares tienen el mismo diámetro.[1] Las funciones lemniscáticas elípticas son las análogas a las funciones trigonométricas para la lemniscata de Bernoulli, y las constantes de la lemniscata surgen al calcular la longitud de arco de este curva.
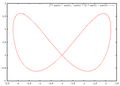
Lemniscata de Gerono

Otra lemniscata, la lemniscata de Gerono o lemniscata de Huygens, es el conjunto de ceros del polinomio cuártico .[6][7] La curva de Viviani, una curva tridimensional formada por la intersección de una esfera con un cilindro, también tiene una figura de ocho, y toma la forma de la lemniscata de Gerono cuando se proyecta sobre un plano.[8]
Otras
Otras curvas algebraicas en forma de figura ocho incluyen:
- La curva del diablo, una curva definida por la ecuación cuártica , una de cuyas componentes conexas tiene forma de ocho,[9]
- Curva de Watt, una curva con forma de ocho generada por un enlace mecánico. La curva de Watt es el conjunto de ceros de la ecuación polinomial de grado seis e incluye a la lemniscata de Bernoulli como un caso especial.
- Besace, curva estudiada por Gabriel Cramer, con la ecuación o , con .
Generalización
En geometría analítica, considérese n puntos del plano F1, F2, ...,Fn y k un número real estrictamente positivo. El conjunto de los puntos del plano cuyo producto de las distancias a cada uno de los puntos F1, F2,...,Fn es constante e igual a k es una curva (lugar geométrico) llamada lemniscata de n focos.[10] La lemniscata de Bernoulli tiene solo dos focos.[11]
Una lemniscata de un solo foco es una circunferencia.
Lemniscata en el plano complejo
La ecuación de la lemniscata en el plano complejo es
Propiedades
Una secuencia arbitraria puede aproximarse a una curva arbitraria. En particular, al tomar un número diferente de focos, organizarlos de manera diferente y asignar uno u otro valor para producir distancias, se pueden obtener los elementos más extraños, por ejemplo, el contorno de una cabeza humana o un ave.
Ejemplos
- Diversos ejemplos de lemniscatas
-
Lemniscata de Bernoulli
-
Lemniscata de Gerono
-
Lemniscata de Booth
-
Curva del diablo
-
Besace
Véase también
- Analema, la curva en forma de figura de ocho trazada por las posiciones al mediodía del sol en el cielo durante un año
- Atractor de Lorenz, un sistema dinámico tridimensional que exhibe la forma de una lemniscata
- Lemniscatas como cónicas generalizadas
Referencias
- ↑ a b c d Schappacher, Norbert (1997), «Some milestones of lemniscatomy», Algebraic Geometry (Ankara, 1995), Lecture Notes in Pure and Applied Mathematics 193, New York: Dekker, pp. 257-290, MR 1483331..
- ↑ a b Erickson, Martin J. (2011), «1.1 Lemniscate», Beautiful Mathematics, MAA Spectrum, Mathematical Association of America, pp. 1-3, ISBN 9780883855768..
- ↑ Bos, H. J. M. (1974), «The lemniscate of Bernoulli», For Dirk Struik, Boston Stud. Philos. Sci., XV, Dordrecht: Reidel, pp. 3-14, ISBN 9789027703934, MR 774250..
- ↑ Langer, Joel C.; Singer, David A. (2010), «Reflections on the lemniscate of Bernoulli: the forty-eight faces of a mathematical gem», Milan Journal of Mathematics 78 (2): 643-682, MR 2781856, doi:10.1007/s00032-010-0124-5..
- ↑ Köller, Jürgen. «Acht-Kurve». www.mathematische-basteleien.de. Consultado el 26 de noviembre de 2017.
- ↑ Basset, Alfred Barnard (1901), «The Lemniscate of Gerono», An elementary treatise on cubic and quartic curves, Deighton, Bell, pp. 171-172..
- ↑ Chandrasekhar, S (2003), Newton's Principia for the common reader, Oxford University Press, p. 133, ISBN 9780198526759..
- ↑ Costa, Luisa Rossi; Marchetti, Elena (2005), «Mathematical and Historical Investigation on Domes and Vaults», en Weber, Ralf; Amann, Matthias Albrecht, eds., Aesthetics and architectural composition : proceedings of the Dresden International Symposium of Architecture 2004, Mammendorf: Pro Literatur, pp. 73-80..
- ↑ Darling, David (2004), «devil's curve», The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, pp. 91-92, ISBN 9780471667001..
- ↑ "Diccionario de matemáticas" (2001) Espinosa de los Monteros, Julián, Coordinador general. ISBN 84-8055-355-3, pg.168
- ↑ " Geometría Analítica" (1968) Rey Pastor, Julio; Santaló, Luis; Balanzat, Manuel. Sin ISBN. pág. 195
Enlaces externos
- Hazewinkel, Michiel, ed. (2001), «Lemniscata», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.