Michelson-Morley esperimentua

Michelson-Morley esperimentua fisikaren historiako garrantzitsu eta ospetsuenetako bat izan zen. 1887an, Albert Abraham Michelsonek (Fisikako Nobel Saria, 1907[1]) eta Edward Morleyk egin zuten, haien esperimentuak eterraren ez-existentzia frogatu zuen.
Lurraren higidura erlatiboa detektatzeko helburua zuen hutsunea bete behar zuen argi-eterren bidez, eta uhin elektromagnetikoen hedapenaren euskarria zen[2]. Erabilitako metodoa argiaren Lurraren translazio-mugimenduaren norabidean abiadura neurtzea izan zen, eta, aldi berean, noranzko perpendikularrean. Neurketa egileek diseinatutako interferometro batekin interferentzia-eredu bat behatuz egin zen.
Esperimentu horren emaitza negatiboak orduan indarrean zegoen eterraren teoriaren aurkako lehen froga sendotzat hartzen dira, eta Albert Einsteinen Erlatibitate Bereziaren Teoria 1905ean formulatu zuen ikerketa-lerro bat hasi zen, non eter geldikorraren kontzeptuak ez du inolako paperik jokatzen.
Motibazioa
XIX. mendearen amaierako teoriak postulatzen zuen uhinak eta soinuak hedatzeko euskarri bat behar duten bezala (ura edo airea, esaterako), argiak ere medio bat beharko lukeela, eter izenekoa. Argiaren abiadura oso handia denez, eteraren presentzia detektatzeko esperimentu bat diseinatzea oso zaila zen.

Michelson eta Morleyren helburua Lurra eterarekiko mugitzen den abiadura erlatiboa neurtzea zen.
Urtero, Lurrak distantzia izugarria egiten du Eguzkiaren orbitan inguruan, 30 km/s-ko abiaduran (100.000 km/h baino gehiago). Gure izarren posizioarekiko (eguzkiarekiko) eter-haizearen norabidea, Lurretik neurtzean, aldatu egingo zela uste zen eta horrela detektatua izan zitekeela. Hori dela eta, eta espazioan Eguzkiak haizean izan zitzakeen ondorioak saihesteko, esperimentua urteko hainbat sasoitan egin beharko litzateke.
Eter-haizeak uhin argiengan duen eragina ibai-korronteak berarekin edo aurka mugitzen den igerilari batengan bezalakoa izango litzateke. Momentu batzuetan, igerilaria moteldu egingo zen, eta, beste batzuetan, bultzatua. Eterarekiko posizio ezberdinetan Lurrera iristean, argiarekin hau gertatuko zela uste zen: abiadura ezberdinetan iritsi beharko litzateke. Gakoa da, bidaia zirkularretan abiadura-aldea oso txikia dela, segundo baten milioirenaren ingurukoa. Hala ere, Michelsonek, argiaren abiadura neurtzeko esperientzia handikoa, minutuko diferentzia hori neurtzeko modu bat asmatu zuen.
Esperimentuaren deskribapena

A - Argi iturri monokromatikoa B - Ispilu erdi islatzailea C - Ispiluak D - Bide-aldea.
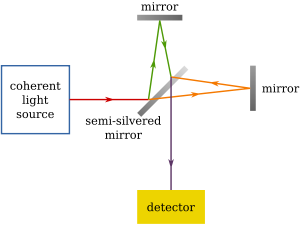
Itsas mailatik gertu dagoen eraikin baten oinarrian, Michelsonek eta Morleyk Michelson interferometroa deritzona eraiki zuten. Erdi zilarrezko edo erdi ispiluko lente batez osatuta dago, argi monokromatikoa elkarren artean angelu jakin batean bidaiatzen duten bi argi izpitan banatzen duena.
Horren bidez, posible zen aldi berean bi argi izpi (iturri beretik sortuak) norabide perpendikularrean bidaltzea, distantzia berdinak (edo bide optiko berdinak) ibiltzea eta puntu komun batean biltzea, non interferentzia-eredu bat sortzen den argiaren abiaduraren araberakoa interferometroaren bi besoetan. Abiadura horren edozein diferentzia (argiak eterraren mugimenduarekiko duen mugimenduaren noranzko ezberdinek eragindakoa) detektatuko litzateke.
Ispiluen eta ispilu erdiaren arteko distantziak "L" luzera du, hau da, "1 bidaia" "2 bidaia"ren berdina da.
1. eta 2. ibilaldien arteko desberdintasuna dago Lurretik eta Lurretik kanpo (kanpoko behatzailea) behatutakoan. Atsedenaldian dagoen kanpoko behatzailearen (planetatik kanpo) bideak hauek izango dira:
Zein:
Ondoren, hau dauka:
Azkenik, 1 bidaia sinplifikatu ondoren lortzen dugu:
2 bidaia lortzeko, honako hauek ditugu (Ikus 3. irudia):
t1 eta t2 aurkitzeko onar daiteke irteeran (t1) argia c-v abiaduran doala eta distantzia oraindik L dela, eta antzera itzulerako (t2) abiadura c+v eta distantzia L dela suposa daiteke. Orduan hau dugu: t1=l/(c-v) eta t2=l/(c+v):
- Itsasontziak korrontearen alde eta korrontearen kontra emandako denbora, Michelson eta Morleyren interpretazioaren arabera, honako hauek emango luke:
- Itsasontziak angelu zuzen batean mugitzen duen denbora, Michelsonentzat eta Morleyrentzat hau da:
- Denboraren aldea honako hau izango litzateke:
- =
- Lorentz uzkurdura goian adierazitako formula matematikoen ondorioa da. Adierazpen honek adierazten duen uzkurdura:
- ,
non L1 "v" abiadurarekin higitzen den behatzaileak neurtzen duen distantzia den non "c" argiaren abiadura den eta L2 geldian dagoen behatzaile batek neurtzen duen distantzia den, eta, aztertzen ari den interferometroaren kasuan, uzkurdura bere besoetako baten luzera murriztearekin bat etorriko litzateke, eta horrek azalduko luke argi-izpi biak aldi berean helmugara iristeko arrazoia (fasean iristen ziren).
Michelsonek eta Morleyk erabilitako analogiak bi itsasontzi, ibai bat eta behatzaile bat aipatzen ditu.
| Ikertzailea | Esperimentuaren urtea | L 1 eta L 2 interferometroaren beso bakoitzeko metroak | ertz-aldaketa aurreikusia | Behatutako txandakako goiko muga | Lekua | Goiko muga V eterrarena | Iragarri v/s Behatua % | Oharrak |
|---|---|---|---|---|---|---|---|---|
| Michelson | 1881 | 1.2 | 0.4 | 0,02 | Potsdam | % 5 | (A) | |
| Michelson eta Morley | 1887 | 11.0 | 0.4 | <0,01 | Cleveland | 8 km/s | % 2,5 | (B) |
| Morley eta Miller | 1902-1904 _ | 32.2 | 1.13 | 0,015 | Cleveland | % 1,33 | ||
| Miller | 1921 | 32.0 | 1.12 | 0,08 | mt wilson | % 7,14 | ||
| Miller | 1923-1924 _ | 32.0 | 1.12 | 0,03 | Cleveland | % 2,68 | ||
| Miller (eguzki argia) | 1924 | 32.0 | 1.12 | 0,014 | Cleveland | % 1,25 | ||
| Tomascheck (izar argia) | 1924 | 8.6 | 0.3 | 0,02 | Heidelberg | % 6 | ||
| Miller | 1925-1926 _ | 32.0 | 1.12 | 0,088 | mt wilson | % 7,86 | ||
| Kennedy ( Wilson mendia ) | 1926 | 2.0 | 0,07 | 0,002 | Pasadena eta Mt. Wilson | % 2,85 | ||
| illingworth | 1927 | 2.0 | 0,07 | 0,0002 | pasadena | 1 km/s | % 0,285 | |
| Piccard eta Stahel ( Rigi ) | 1927 | 2.8 | 0,13 | 0,006 | Rigi mendia | % 4,62 | ||
| Michelson et al. | 1929 | 25.9 | 0,9 | 0,01 | mt wilson | % 1,12 | ||
| Joos | 1930 | 21.0 | 0,75 | 0,002 | jena | % 0,267 |
Erreferentziak
- ↑ «Albert A. Michelson - Facts» www.nobelprize.org.
- ↑ Morley, Albert Abraham Michelson and Edward. On the Relative Motion of the Earth and the Luminiferous Ether. (Noiz kontsultatua: 2022-12-19).












