Tangente (trigonometria)

Tangentea (laburtuta tan edo tg) aurkako katetoaren eta ondoko katetoaren arteko arrazoia da.

${\displaystyle \operatorname {tg} \,\alpha ={\frac {\overline {CB}{\overline {AC}={\frac {a}{b}$

Arrazoi honen tamainak ez du zerikusirik aukeratuta triangeluaren tamainarekin, baizik eta angeluaren balioarekin.

Historia

Regiomontano izan zen, ziurrenik, Europan trigonometria matematikako adar ezberdindu gisa landu zuen lehenengoa. De triangulis omnimodis lanean, 1464koa, eta Tabluae directionumen, beranduago, funtzio tangentea aipatzen zuen, nahiz eta izenik ez zion eman^[1].

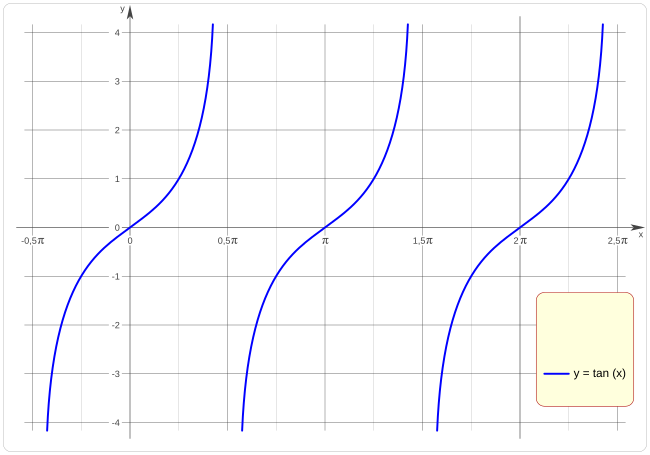
Irudikapen grafikoa

Identitateak

Bi angeluen baturaren tangentea

Identitate trigonometriko hau bi angeluren batuketaren identitatetik abiatzen da, dagoeneko sinu eta kosinuarentzat ezagutzen dena.

• ${\displaystyle \phi ,\theta \ }$ angeluak izanda:

${\displaystyle \operatorname {tg} \left(\phi +\theta \right)={\cfrac {\operatorname {sen}(\phi +\theta )}{\cos(\phi +\theta )}$

• Lehengo identitateengatik ordezkatuta:

${\displaystyle \operatorname {tg} \left(\phi +\theta \right)={\cfrac {\operatorname {sen} \phi \cos \theta +\cos \phi \operatorname {sen} \theta }{\cos \phi \cos \theta -\operatorname {sen} \phi \operatorname {sen} \theta }$

• Zatikiaren aldeak ebatziz ${\displaystyle \cos \phi \cos \theta \,}$:

${\displaystyle \operatorname {tg} \left(\phi +\theta \right)={\cfrac {\cfrac {\operatorname {sen} \phi \cos \theta +\cos \phi \operatorname {sen} \theta }{\cos \phi \cos \theta }{\cfrac {\cos \phi \cos \theta -\operatorname {sen} \phi \operatorname {sen} \theta }{\cos \phi \cos \theta }$

Bi angeluaren kenketaren tangentea

• ${\displaystyle \operatorname {tg} \left(\phi +(-\theta )\right)={\frac {\operatorname {tg} \phi +\operatorname {tg} (-\theta )}{1-\operatorname {tg} \phi \operatorname {tg} (-\theta )}$

• Funtzi bakoitia denez, hau lortzen da:

${\displaystyle \operatorname {tg} \left(\phi -\theta \right)={\frac {\operatorname {tg} \phi -\operatorname {tg} \theta }{1+\operatorname {tg} \phi \operatorname {tg} \theta }$

Formula laburtua

${\displaystyle \operatorname {tg} \left(\phi \pm \theta \right)={\frac {\operatorname {tg} \phi \pm \operatorname {tg} \theta }{1\mp \operatorname {tg} \phi \operatorname {tg} \theta }$

Angelu bikoitzaren tangentea

Hemendik abiatuz

${\displaystyle \operatorname {tg} \left(\phi +\theta \right)={\frac {\operatorname {tg} \phi +\operatorname {tg} \theta }{1-\operatorname {tg} \phi \operatorname {tg} \theta }$

eta ${\displaystyle \phi =\theta \,}$ eginez, orduan:

${\displaystyle \operatorname {tg} \left(2\phi \right)={\frac {2\operatorname {tg} \phi }{1-\operatorname {tg} ^{2}\phi }$

Angelu hirukoitzaren tangentea

ψ angeluaren tangentea ezagututa, 3ψ tangentea aurkitu:

${\displaystyle \operatorname {tg} \left(3\psi \right)={\frac {3\operatorname {tg} \psi -\operatorname {tg} ^{3}\psi }{1-3\operatorname {tg} ^{2}\psi }$

Angelu erdiaren tangentea aurkitu

θ angeluaren erdiaren tangentea aurkitu:

${\displaystyle \operatorname {tg} {\frac {\theta }{2}={\frac {\operatorname {sen} \theta }{1+\cos \theta }$ ^[2]

Tangentearen deribatua

Tangentearen deribatua honela kalkulatzen da:

${\displaystyle [\operatorname {tg} (x)]'=\sec ^{2}(x)\,}$

Erreferentziak

Ikus, gainera

• Sinua
• Kosinua

Kanpo estekak

• Funtzio trigonometrikoak. Hiru.com