رمزنگاری قالبی
در رمزنگاری، رمزنگاری قالبی یک الگوریتم قطعی است که بر روی گروههای بیت با طول ثابت که به عنوان بلاک شناخته میشوند کار میکند، با یک تحول بی وقفه که توسط یک کلید متقارن مشخص شدهاست. رمزنگاریهای قالبی به عنوان مؤلفههای ابتدایی مهم در طراحی بسیاری از پروتکلهای رمزنگاری عمل میکنند و بهطور گستردهای برای پیادهسازی رمزگذاری دادههای زیاد مورد استفاده قرار میگیرند.
حتی رمزنگاری قالبی ایمن فقط برای رمزگذاری یک بلوک واحد در زیر یک کلید ثابت مناسب است. بسیاری از حالتهای عملکردی طراحی شدهاند تا استفاده مکرر آنها را به روشی مطمئن و معمولاً برای دستیابی به اهداف امنیتی مانند محرمانه بودن و اعتبارسنجی امکان بذیر کنند. با این حال، رمزنگارهای قالبی ممکن است به عنوان بلوکهای ساختاری در سایر پروتکلهای رمزنگاری شده، مانند توابع آمیزش جهانی و تولیدکننده شماره شبه تصادفی نیز ظاهر شوند.
تعریف
رمزنگاری قالبی از دو الگوریتم زوج تشکیل شده است، یکی برای رمزگذاری، E و دیگری برای رمزگشایی، D[۱] هر دو الگوریتم دو ورودی را قبول میکنند: یک بلوک ورودی از بیت اندازه n و یک کلید از بیت اندازه k. و هر دو بلوک خروجی n -bit دارند. الگوریتم رمزگشایی D تعریف شدهاست که عملکرد معکوس رمزگذاری است، یعنی D = E^(-1).[۲][۳] رمزگذاری بلوک توسط یک عملکرد رمزگذاری مشخص میشود.
که به عنوان ورودی کلید K از طول بیت k، به نام اندازه کلید و یک bit string به نام P از طول n به نام اندازه بلوک را در نظر میگیرد و یک رشته C از n بیتها را برمیگرداند. P به متن ساده گفته میشود و C به متن متن رمزگذاری میشود. برای هر K، عملکرد EK (P) لازم است که یک نگاشت معقول با {۰،1} n باشد. معکوس برای E به عنوان یک تابع تعریف میشود
با استفاده از یک کلید K و ciphertext که C باشد برای برگرداندن مقدار plaintext که با P نمایش میدهیم، به این ترتیب:
به عنوان مثال، یک الگوریتم رمزنگاری شده ممکن است یک متن ۱۲۸ بیتی از متن ساده را به عنوان ورودی بدست آورد، و یک بلوک متن رمزگذاری متناظر ۱۲۸ بیتی را تولید کند. کلید تحریر دقیق با استفاده از یک ورودی دوم کنترل میشود. رمزگشایی مشابه است: الگوریتم رمزگشایی، در این مثال یک بلوک ۱۲۸ بیتی متن رمزنگاری را همراه با کلید مخفی میگیرد و بلوک ۱۲۸ بیتی متن ساده را بازده میکند.
برای هر کلید K , EK مجوز (نقشهبرداری بیولوژیکی) بر روی مجموعه بلوکهای ورودی است. هر کلید یک مجوز از مجموعه (۲ به توان n) جایگشت احتمالی را انتخاب میکند.
تاریخچه
طراحی مدرن رمزنگاریهای قالبی مبتنی بر مفهوم رمزنگاری محصول تکراری است. کلود شانون انتشارات اصلی خود در سال ۱۹۴۹ با عنوان نظریه ارتباطات سیستمهای رازداری، رمزنگاری محصولات را مورد تجزیه و تحلیل قرار داد و با ترکیب عملیات ساده مانند تعویضها و جابجاییها، آنها را به عنوان ابزاری برای بهبود مؤثر امنیت در نظر گرفت. رمزنگاریهای محصول Iterated رمزگذاری را در چند دور انجام میدهند، که هر یک از آنها از یک کلید فرعی متفاوت برگرفته از کلید اصلی استفاده میکند. اجرای گسترده چنین رمزهایی، به نام شبکه فیستل پس از Horst Feistel، به ویژه در رمزگذاری DES پیادهسازی شدهاست.[۴] بسیاری از تحقق رمزنگاریهای قالبی، مانند AES، به عنوان شبکههای جایگزینی-permutation طبقهبندی میشوند. [۵]
ریشه کلیه قالبهای بلوک رمزنگاری شدهای که در استانداردهای امنیت دادههای کارتهای صنعت پرداخت (PCI DSS) و استانداردهای مؤسسه ملی استاندارد آمریکا (ANSI) استفاده میشود مربوط به بلوک کلیدی Atalla (AKB) است که نوآوری اساسی در Atalla Box بود، اولین ماژول امنیتی سختافزار (HSM). این کار در سال ۱۹۷۲ توسط Mohamed M. Atalla، بنیانگذار شرکت Atalla Corporation (در حال حاضر Utimaco Atalla) توسعه یافته و در سال ۱۹۷۳ منتشر شد. AKB یک بلوک کلیدی بود که برای تبادل ایمن کلیدهای متقارن یا پینها با سایر بازیگران صنعت بانکداری مورد نیاز است. این تعویض امن با استفاده از فرمت AKB انجام میشود.[۶] Atalla Box بیش از ۹۰٪ از کل شبکههای دستگاههای خودپرداز را که از سال ۱۹۹۸ کار میکردند محافظت میکرد،[۷] و محصولات Atalla هنوز هم اکثر معاملات ATM جهان را از سال ۲۰۱۴ تضمین میکنند.[۸]
انتشار رمزگذاری DES توسط دفتر ملی استاندارد ایالات متحده (متعاقباً موسسه ملی استاندارد و فناوری NIST) در سال ۱۹۷۷ در درک عمومی از طراحی رمزنگاری مدرن بسیار مؤثر بود. همچنین بر پیشرفت آکادمیک حملات کریپتانالیستی تأثیر گذاشت. cryptanalyse دیفرانسیل و خطی هر دو ناشی از مطالعات در مورد طراحی DES است. تا تاریخ ۲۰۱۶[بروزرسانی] یک مجموعه از تکنیکهای حمله وجود دارد که علاوه بر اینکه در برابر حملات بی رحمانه نیرومند است، باید رمزنگاری قالبی را نیز ایمن کند.
طراحی
رمزگذاریهای Feistel
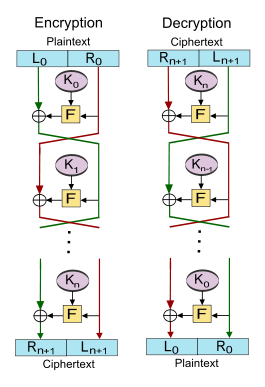
در Feistel cipher,، بلوک plain text برای رمزگذاری به دو نیمه مساوی تقسیم میشود. تابع round با استفاده از یک کلید فرعی روی یکنیمه اعمال میشود، و سپس خروجی با نیمه دیگر XOR میشود. سپس دو نیمه جابهجا میشوند.
فرض کنید F یک تابع round باشد و فرض کنید کلیدهای K0، K1، …، Kn به ترتیب زیر کلیدهای دورهای ۰، …، n باشند.
سپس عملیات اساسی به شرح زیر است:
بلوک متن ساده را به دو قطعه مساوی تقسیم کنید، (، )
برای هر دور به ازای محاسبه کنید
بعد از آن ciphertext برابر است.
رمزگشایی متن رمزنگاری (Rn + 1، Ln + 1) با محاسبه به ازای هر یک از iها انجام میشود
سپس (L0، R0) دوباره plaintext است.
یکی از مزایای مدل Feistel در مقایسه با یک شبکه جایگزینی-جایگشتی این است که تابع round (یا F) نیازی به برگشتناپذیر بودن ندارد.
رمزگذاریهای Lai–Massey
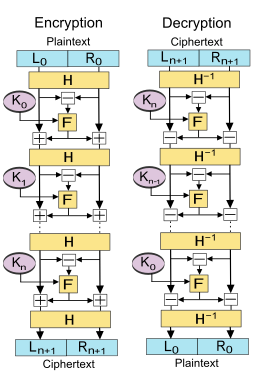
طرح Lai–Masseyخواص امنیتی شبیه به ساختار Feistel را ارائه میدهد. همچنین این مزیت را دارد که تابع round (یا همان F) نیازی به برگشتناپذیر بودن ندارد. شباهت دیگر این است که بلوک ورودی را به دو قطعه مساوی تقسیم میکند. با این حال، تابع round به اختلاف بین این دو اعمال میشود و سپس نتیجه به هر دو نیم بلوک اضافه میشود.
فرض کنید F یک تابع round و H یک تابع half-round باشد و فرض کنید کلیدهای K0، K1، …، زیرکلید برای دورهای ۰٬۱، …، n باشند.
سپس عملیات اساسی به شرح زیر است:
بلاک plaintext را به دو قسمت مساوی تقسیم کنید، (، )
برای هر دور به ازای محاسبه کنید:
هرجا و
سپس عبارت ciphertext برابر است.
رمزگشایی یک ciphertext با محاسبه برای i = n , n − ۱، …، ۰ انجام میشود.
هرجا و
سپس دوباره برابر plaintext است.
عملگرها
ARX (add-rotate-XOR)
بسیاری از رمزگذارها و رمزنگاریهای قالبی مدرن درواقع الگوریتمهای ARX هستند. تابع round آنها فقط شامل سه عمل است: تابع addition یا جمع، rotation با مقادیر چرخش ثابت و XOR (به اختصار ARX). مثالهای آن شامل ChaCha20، Speck , XXTEA و BLAKE است. بسیاری از نویسندگان برای نشان دادن چنین round function ای، از یک شبکه ARX، نوعی نمودار جریان داده ترسیم می کنند.[۹]
این عملگرهای ARX محبوب هستند زیرا از نظر سختافزاری و نرمافزاری نسبتاً سریع و ارزان هستند، اجرای آنها میتواند بسیار ساده انجام شود، همچنین به دلیل اینکه در زمان ثابت اجرا می شون؛ بنابراین در مقابل حملات زمانبندی مصون هستند. روش رمزنگاری چرخشی سعی در حمله به چنین round functionsهایی دارد.
سایر عملگرها
عملگرهای دیگری که اغلب در رمزنگاریهای قالبی مورد استفاده قرار میگیرند شامل: data-dependent rotations مانند RC5 و RC6 است، یک جعبه جایگزینی که به عنوان جدول جستجو (یا lookup table) به کار میرود همانطور که در استاندارد رمزگذاری دادهها و استاندارد رمزگذاری پیشرفته، جعبه جایگشت و ضرب مانند IDEA است.
تحلیل رمزنگاری
حملات Brute-force
این خاصیت باعث میشود امنیت رمزنگاری به صورت درجه یک کاهش یابد و در هنگام انتخاب اندازه بلوک باید مورد توجه قرار گیرد. در واقع یک مصالحه بین بزرگی سایز بلوک و ناکارآمدی الگوریتم به منظور عملکرد عملگر وجود دارد.[۱۰] رمزنگاریهای قالبی اولیه مانند DES معمولاً اندازه بلوک ۶۴ بیتی را انتخاب کردهاند، در حالی که طرحهای جدیدتر مانند AES با اندازه بلوک ۱۲۸ بیت یا بیشتر را پشتیبانی میکنند، در حالی که برخی از رمزگذارها، طیف وسیعی از اندازههای مختلف بلوک را پشتیبانی میکنند.[۱۱]
تحلیل رمزنگاری خطی
نوعی از تحلیل رمزنگاری است که بر اساس یافتن تقریبهای وابسته به پیوند به عملکرد رمزنگاری است. تحلیل رمزنگاری خطی یکی از دو حمله پرکاربرد بر روی رمزنگاریهای قالبی است. دیگری تحلیل رمزنگاری انتگرال است.
این کشف به Mitsuru Matsui منتسب شدهاست، که نخستین بار این تکنیک را در رمزگذاری FEAL به کار برد (Matsui and Yamagishi، ۱۹۹۲).
تحلیل رمزنگاری انتگرالی
یک حمله کریپتانالیستی است که خصوصاً برای مسدود کردن رمزها بر اساس شبکههای جایگزینی-جابجایی کاربرد دارد. برخلاف تحلیل رمزنگاری دیفرانسیل، که از جفتهای plaintexts انتخاب شده با اختلاف XOR ثابت استفاده میکند، تحلیل رمزنگاری انتگرالی از
مجموعهها یا حتی چند مجموعه از plaintexts منتخب استفاده میکند که قسمتی از آن ثابت نگه داشته میشود و بخش دیگر با تمام امکانات متفاوت است. به عنوان مثال، یک حمله ممکن است از ۲۵۶ عدد انتخاب شده استفاده کند که تمام ۸ بیت آنها یکسان است، اما همه در ۸ بیت متفاوت هستند. چنین مجموعه ای لزوماً یک XOR با مقدار ۰ و نیز XORهایی که مقادیر آنها از مجموعههای مربوط به رمزنگاریها، اطلاعات مربوط به عملکرد رمزنگاری را ارائه میدهند، دارد. این تقابل بین تفاوتهای جفت متون و مجموع مجموعههای بزرگتر از متن، الهام بخش از نام «تحلیلی رمزنگاری انتگرالی» و قرض گرفتن اصطلاح آن از حساب دیفرانسیل و انتگرال است. [نیازمند منبع]
تکنیکهای دیگر

علاوه بر تحلیل رمزنگاری خطی و دیفرانسیل، یک فهرست از حملات فزاینده وجود دارد: تحلیل رمزنگاری دیفرانسیل کوتاه، تحلیل رمزنگاری دیفرانسیل جزئی، کریپتانالیز یکپارچه، که شامل حملات مربعی و انتگرالی، حملات اسلاید، حملات بومرنگ، حمله ایکساسال، تحلیل رمزنگاری دیفرانسیل غیرممکن و حملات جبری.
برای اینکه یک رمزنگاری جدید از اعتبار برخوردار باشد، باید شواهد امنیتی را در برابر حملات شناخته شده نشان دهد. [نیازمند منبع]
امنیت قابل تأمین
هنگامی که از یک رمزنگاری قالبی در یک حالت معین از عملکردهای آن استفاده میشود، الگوریتم حاصل بهطور ایدهآل میتواند به اندازه خود رمزنگاری قالبی امن باشد. ECB (مورد بحث در بالا) بهطور برجسته فاقد این خاصیت است: صرف نظر از اینکه رمزنگاریهای قالبی زیرین چقدر امن است، حالت ECB به راحتی میتواند مورد حمله قرار گیرد. از طرف دیگر، با فرض اینکه رمزنگاری قالبی زیرین نیز به همان نسبت امن است، میتوان حالت CBC را ایمن اعلام کرد. با این حال توجه داشته باشید که اظهارنظرهایی مانند این، نیاز به تعاریف رسمی ریاضی دارد که برای آنچه از آن به عنوان الگوریتم رمزگذاری یا رمزنگاری قالبی یاد میشود به معنای «ایمن بودن» است. در این بخش دو مفهوم رایج در مورد خصوصیات رمزنگاری قالبی توضیح داده شدهاست. هر یک با یک مدل ریاضی مطابقت دارد که میتواند برای اثبات خواص الگوریتمهای سطح بالاتر مانند CBC استفاده شود.
این رویکرد کلی در مواجهه با رمزنگاری - اثبات الگوریتمهای سطح بالاتر (مانند CBC) با فرضیههای صریح بیان شده در مورد اجزای آنها (مانند رمزنگاری قالبی) ایمن است - به عنوان امنیت قابل اثبات شناخته شده است.
مدل استاندارد
اگر مهاجمی نتواند تفاوت بین رمزنگاری قالبی (مجهز به کلید تصادفی) و یک جابجایی تصادفی را نشان دهد، یک رمزنگاری قالبی در مدل استاندارد ایمن است.
برای دقیق تر بودن، فرض کنید E یک رمزنگاری قالبی n -bit ای باشد. ما بازی زیر را تصور میکنیم:
- شخصی که بازی را اجرا میکند، یک سکه را به هوا میاندازد.
- مهاجم رشتهٔ X که n-bit دارد را انتخاب میکند و شخصی که بازی را انجام میدهد مقدار f (X) را به او میگوید.
- مرحله ۲ در کل q بار تکرار میشود. (هر یک از این فعل و انفعالات q یک واکشی است .)
- مهاجم حدس میزند که چگونه سکه به زمین فرود آمدهاست. اگر حدس او صحیح باشد، برنده میشود.
مهاجم، که میتوانیم آن را به عنوان یک الگوریتم در نظر بگیریم، یک دشمن نامیده میشود. تابع f (که طرف مقابل قادر به جستجوی آن بود) اوراکل نامیده میشود.
توجه داشته باشید که یک دشمن میتواند با حدس زدن تصادفی (یا مثلاً همیشه «رو» را حدس بزند) شانس ۵۰٪ پیروزی را تضمین کند؛ بنابراین، فرض کنید P E (A) این احتمال را نشان دهد که طرف A در این بازی درمقابل E برنده شود و سود A را به شکل مقابل تعریف کند (P E (A)-1/2)2.
به این ترتیب که اگر A به طور تصادفی حدس بزند، سود آن ۰ خواهد بود. از طرف دیگر، اگر A همیشه برنده باشد، سود آن ۱ است. رمزنگاری قالبی E با توجه به محدودیتهای مشخص شده در q و زمان اجرای طرف مقابل، اگر دارای جا به جایی شبه تصادفی (PRP) باشد، هیچ حریفی با سود قابل بیشتر از ۰ نخواهد داشت. اگر در مرحله ۲، دشمنان به جای f (X) از یادگیری f −1 (X) استفاده کنند (اما هنوز تنها سود کمی دارند)، آنگاه E یک PRP قوی (SPRP) است. یک مهاجم غیر انطباقی است اگر همه مقادیر q برای X را قبل از بازی انتخاب کند (یعنی از اطلاعاتی که از نمایشهای قبلی استفاده نشدهاست، برای انتخاب هر X در هر صورت استفاده میکند).
این تعاریف برای تجزیه و تحلیل حالتهای مختلف عملگر مفید بودهاست. به عنوان مثال، میتوان یک بازی مشابه را برای اندازهگیری امنیت الگوریتم رمزنگاری مبتنی بر رمزنگاری قالبی تعریف کرد و سپس سعی کرد (از طریق یک استدلال کاهشی) نشان داد که احتمال برنده شدن حریف در این بازی جدید، خیلی بیشتر از PE(A) برای A نیست. (کاهش بهطور معمول محدودیتهایی در q و زمان اجرای A را در اختیار شما قرار میدهد.) بهطور برابر، اگر مقدار P E (A) برای همه Aهای مربوط کم باشد، پس هیچ مهاجمی احتمال قابل توجهی برای برنده شدن در بازی جدید ندارد. درواقع این ایده را رسمیت میبخشد که الگوریتم سطح بالاتر امنیت رمزنگاری قالبی را به ارث میبرد.
رمزنگاریهای قالبی قابل توجه
IDEA
الگوریتم رمزگذاری دادههای بینالمللی (IDEA) یک رمزنگاری است که توسط James Massey از مؤسسه فناوری فدرال زوریخ و Xuejia Lai طراحی شدهاست. اولین بار در سال ۱۹۹۱ به عنوان جایگزینی برای DES توصیف شد.
IDEA با استفاده از یک کلید ۱۲۸ بیتی بر روی بلوکهای ۶۴ بیتی کار میکند، و شامل یک سری از هشت تبدیل یکسان (یک round) و یک دگرگونی خروجی (half-round) است. فرایندهای رمزگذاری و رمزگشایی مشابه هستند. IDEA بخش اعظم امنیت خود را با در هم آمیختن عملیات از گروههای مختلف - اضافه شدن و ضرب ماژولار، و منحصر به فرد بصری یا (XOR) - که از نظر جبری «ناسازگار» هستند، به دست میآورد.
طراحان IDEA را برای اندازهگیری استحکام آن در برابر تحلیل رمزنگاری دیفرانسیل بررسی کردند و به این نتیجه رسیدند که تحت فرضیات خاصی از آن مصون است. هیچ ضعف خطی یا جبری موفقیتآمیزی گزارش نشدهاست. تا تاریخ ۲۰۱۲[بروزرسانی] بهترین حمله برای کلیه کلیدها میتواند با استفاده از یک حمله narrow-bicliques حدود چهار برابر سریعتر از حمله brute force، یک IDEA که 8.5-round است را کامل بشکند.
RC5

RC5 رمزنگاری قالبی استکه توسط رونالد ریوست در سال ۱۹۹۴ طراحی شدهاست و برخلاف بسیاری از رمزگذارهای دیگر، اندازه بلوک متغیر (۳۲، ۶۴ یا ۱۲۸ بیت)، اندازه کلید (۰ تا ۲۰۴۰ بیت) و تعداد دور (۰ تا ۲۵۵) دارد. انتخاب اصلی پارامترها اندازه بلوک ۶۴ بیت، یک کلید ۱۲۸ بیتی و 12 round بود.
ویژگی اصلی RC5 استفاده از چرخش وابسته به دادهها است. یکی از اهداف RC5، فوریت مطالعه و ارزیابی چنین عملیاتی به عنوان رمزنگاری اولیه بود. RC5 همچنین شامل تعدادی اضافات ماژولار و XOR است. ساختار کلی الگوریتم یک شبکه شبیه Feistel است. روال رمزگذاری و رمزگشایی را میتوان در چند خط کد مشخص کرد. با این حال، برنامه کلیدی پیچیدهتر است و کلید را با استفاده از one-way function و با باینریهای هر دو e و نسبت طلایی به عنوان منبع nothing up my sleeve numbers گسترش میدهیم. سادگی خسته کننده الگوریتم، همراه با جدید بودن چرخش وابسته به دادهها، RC5 را به یک موضوع جذاب برای مطالعه برای رمزنگاری تبدیل کردهاست.
RC5 که round-12 است (با بلوکهای ۶۴ بیتی) با استفاده از244 نمونه ساده انتخاب شده مستعد حمله دیفرانسیل است.[۱۲] 18-20 round برای محافظت کافی پیشنهاد شدهاست.
Rijndael / AES
رمزگذاری Rijndael که توسط رمزنگاران بلژیکی، Joan Daemen و Vincent Rijmen ساخته شد یکی از طرحهای رقابتی برای جایگزینی DES بود. این طرح در مسابقه 5-year public competition برنده شد تا تبدیل به AES شود ،(استاندارد رمزگذاری پیشرفته).
AES در سال ۲۰۰۱ پذیرفته شده توسط NIST، دارای اندازه بلوک ثابت ۱۲۸ بیت و اندازه کلید ۱۲۸، ۱۹۲ یا ۲۵۶ بیت است، در حالی که Rijndael را میتوان با اندازههای بلوک و کلید در هر چند برابر از ۳۲ بیت، با حداقل ۱۲۸ مشخص کرد. اندازه بلوک حداکثر ۲۵۶ بیت دارد، اما اندازه کلید سایز تئوری حداکثری ندارد. AES در یک ماتریس column-major order عمل میکند، به این حالت گفته میشود (نسخههای Rijndael با اندازه بلوک بزرگتر دارای ستونهای اضافی برای حالت هستند).
جستارهای وابسته
- خلاصه امنیت رمزگذاری
- مباحث مربوط به رمزنگاری
منابع
- ↑ Cusick, Thomas W.; Stanica, Pantelimon (2009). Cryptographic Boolean functions and applications. Academic Press. pp. 158–159. ISBN 978-0-12-374890-4.
- ↑ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (1996). "Chapter 7: Block Ciphers". Handbook of Applied Cryptography. CRC Press. ISBN 0-8493-8523-7. Archived from the original on 3 February 2021. Retrieved 21 May 2020.
- ↑ Bellare, Mihir; Rogaway, Phillip (11 May 2005), Introduction to Modern Cryptography (Lecture notes), chapter 3.
- ↑ van Tilborg, Henk C. A.; Jajodia, Sushil, eds. (2011). Encyclopedia of Cryptography and Security. Springer. ISBN 978-1-4419-5905-8., p. 455.
- ↑ van Tilborg & Jajodia 2011.
- ↑ Rupp, Martin (16 August 2019). "The Benefits of the Atalla Key Block". Utimaco. Archived from the original on 17 October 2020. Retrieved 10 September 2019.
- ↑ Hamscher, Walter; MacWillson, Alastair; Turner, Paul (1998). "Electronic Business without Fear: The Tristrata Security Architecture" (PDF). Semantic Scholar. Price Waterhouse. Archived from the original (PDF) on 25 February 2019. Retrieved 7 October 2019.
- ↑ Stiennon, Richard (17 June 2014). "Key Management a Fast Growing Space". SecurityCurrent. IT-Harvest. Retrieved 21 August 2019.
- ↑ Aumasson, Jean-Philippe; Bernstein, Daniel J. (2012-09-18). "SipHash: a fast short-input PRF" (PDF): 5.
{cite journal}: Cite journal requires|journal=(help) - ↑ Martin, Keith M. (2012). Everyday Cryptography: Fundamental Principles and Applications. Oxford University Press. p. 114. ISBN 978-0-19-969559-1.
- ↑ Paar, Cristof; et al. (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. p. 30. ISBN 978-3-642-04100-6.
- ↑ Biryukov A. and Kushilevitz E. (1998). Improved Cryptanalysis of RC5. EUROCRYPT 1998.
خواندن بیشتر
- Knudsen, Lars R.; Robshaw, Matthew (2011). The Block Cipher Companion. Springer. ISBN 978-3-642-17341-7.





















