فضای تیخونوف

اصول جداسازی در فضاهای توپولوژی
طبقه بندی کولموگوروف
${\displaystyle T_{0}$	(کولموگوروف)
${\displaystyle T_{1}$	(فرشه)
${\displaystyle T_{2}$	(هاسدورف)
${\displaystyle T_{2{\frac {1}{2}$	(اوریسون)
کاملاً ${\displaystyle T_{2}$	(کاملاً هاسدورف)
${\displaystyle T_{3}$	(هاسدورف منظم)
${\displaystyle T_{3{\frac {1}{2}$	(تیخونوف)
${\displaystyle T_{4}$	(هاسدورف نرمال)
${\displaystyle T_{5}$	(کاملاً نرمال/هاسدورف)
${\displaystyle T_{6}$	(نرمال بی‌نقص/هاسدورف)
تاریخچه

در توپولوژی، فضاهای تیخونوف (به انگلیسی: Tychonoff Spaces) و فضاهای کاملاً منظم انواعی از فضاهای توپولوژیکی اند. این شرایط مثال‌هایی از اصول جداسازی می‌باشند.

فضاهای تیخونوف به نام آندری نیکولایویچ تیخونوف نامگذاری شده که نام روسی او Тихонов است که در انگلیسی به صورت‌های "Tychonov" یا "Tikhonov" یا "Tihonov" یا "Tichonov" و … در متون نوشته می‌شود. او کسی بود که این فضاها را در ۱۹۳۰ میلادی به منظور اجتناب از حالت‌های مشکل دار (پاتولوژیکال) فضاهای هاسدورف معرفی کرد، حالت‌هایی که تنها توابع حقیقی مقدار پیوسته آن فضاها، نگاشت‌های ثابت اند.^[۱]

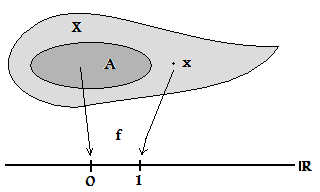
فضایی چون ${\displaystyle X}$ را کاملاً منظم گویند اگر بتوان نقاط آن را با مجموعه‌های بسته و به کمک توابع پیوسته حقیقی مقدار بتوان جداسازی کرد. به بیان دقیق تر یعنی: برای هر مجموعه بسته ${\displaystyle A\setminus X}$ و هر نقطه ${\displaystyle x\in X\setminus A}$، وجود داشته باشد تابع پیوسته حقیقی-مقداری چون ${\displaystyle f\colon X\rightarrow \mathbb {R} }$، چنان‌که ${\displaystyle f(x)=1}$ و ${\displaystyle f\vert _{A}=0}$ . (به‌طور معادل، می‌توان تعریف را به گونه ای تغییر داد که تابع ${\displaystyle f}$ به جای ۰ و ۱ هر دو مقدار دیگری را اختیار کند، یا حتی کاری کرد که ${\displaystyle X}$ کراندار باشد)

یک فضای توپولوژی را فضای تیخونوف (یا فضای ${\displaystyle T_{3{\frac {1}{2}$ یا فضای ${\displaystyle T_{\pi }$ یا فضای کاملاً ${\displaystyle T_{3}$) گویند اگر یک فضای هاسدورف کاملاً منظم باشد.

نکته: فضاهای کاملاً منظم و تیخونوف از طریق مفهوم هم‌ارزی کولموگوروف مرتبط اند. یک فضای توپولوژیکی تیخونوف است اگر هم کاملاً منظم باشد و هم ${\displaystyle T_{0}$ (فضای کولموگوروف). از سوی دیگر، یک فضا کاملاً منظم است اگر و تنها اگر خارج قسمت کولموگوروف آن تیخونوف باشد.

• مشارکت‌کنندگان ویکی‌پدیا. «Tychonoff Space». در دانشنامهٔ ویکی‌پدیای انگلیسی.