Analyse en composantes principales à noyaux

Dans le domaine des statistiques multivariées, l'analyse en composantes principales à noyau (ACP à noyau; en anglais : kernel principal component analysis, KPCA)^[1] est une extension de l'analyse en composantes principales (ACP) utilisant l'astuce du noyau (méthodes à noyau). En utilisant un noyau, les opérations initialement linéaires de l'ACP sont effectuées dans un espace de Hilbert à noyau reproducteur, un espace à grande dimension.

Rappelons que l'ACP conventionnelle fonctionne sur des données centrées sur zéro; c'est-à-dire,

${\displaystyle {\frac {1}{N}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0} }$ ,

où ${\displaystyle \mathbf {x} _{i}$ est l'un des ${\displaystyle N}$ observations multivariées. Il fonctionne en diagonalisant la matrice de covariance,

${\displaystyle C={\frac {1}{N}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }$

en d'autres termes, cela donne une décomposition en éléments propres de la matrice de covariance :

${\displaystyle \lambda \mathbf {v} =C\mathbf {v} }$

qui peut être réécrite comme

${\displaystyle \lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}~i=1,\ldots ,N}$.

(Voir aussi : Matrice de covariance comme opérateur linéaire)

Pour comprendre l'utilité de l'ACP à noyau, en particulier pour le partitionnement de données, observez que, bien que N points ne puissent pas, en général, être séparés linéairement dans ${\displaystyle d<N}$ dimensions, elles peuvent presque sûrement être séparées linéairement dans ${\displaystyle d\geq N}$ dimensions. C'est-à-dire, étant donné N points, ${\displaystyle \mathbf {x} _{i}$, si nous les projetons dans un espace N -dimensionnel avec

${\displaystyle \Phi (\mathbf {x} _{i})}$ où ${\displaystyle \Phi :\mathbb {R} ^{d}\to \mathbb {R} ^{N}$,

il est alors facile de construire un hyperplan qui divise les points en groupes arbitraires. Bien sûr, ce ${\displaystyle \Phi }$ crée des vecteurs linéairement indépendants, il n'y a donc pas de covariance sur laquelle effectuer une décomposition en éléments propres explicitement comme nous le ferions pour une ACP linéaire.

Au lieu de cela, dans l'ACP à noyau, la fonction, arbitraire non trivial, ${\displaystyle \Phi }$ est « choisie » mais elle n'est jamais calculée explicitement. Ceci permet d'utiliser des fonctions de très grande dimension ${\displaystyle \Phi }$ car nous n'avons jamais à évaluer réellement les données dans cet espace. Étant donné que nous voulons éviter de travailler dans le ${\displaystyle \Phi }$ -espace, que nous appellerons « espace de re-description » (feature space, en anglais), nous allons utiliser l'astuce du noyau et créer le noyau N-par-N

${\displaystyle K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )}$

qui représente l'espace du produit interne (voir matrice de Gram) de l'espace de re-description autrement intraitables. La forme duale qui apparaît lors de la création d'un noyau nous permet de formuler mathématiquement une version de l'ACP dans laquelle nous ne résolvons jamais réellement les vecteurs propres et les valeurs propres de la matrice de covariance dans l'espace des ${\displaystyle \Phi (\mathbf {x} )}$ (voir Astuce du noyau). Les N éléments de chaque colonne de K représentent le produit scalaire d'un point des données transformées par rapport à tous les points transformés (N points). Dans la section exemple ci-dessous, nous présentons certains des noyaux les plus utilisés.

Parce que nous ne travaillons jamais directement dans l’espace de re-description, la formulation du noyau de l’ACP est limitée dans la mesure où elle ne calcule pas les composantes principales elles-mêmes, mais les projections de nos données sur ces composantes. Pour évaluer la projection à partir d'un point dans l'espace des fonctions ${\displaystyle \Phi (\mathbf {x} )}$ sur la kème composante principale ${\displaystyle V^{k}$ (où l'exposant k indique composante k, et non V à la puissance k)

${\displaystyle {V^{k}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a} _{i}^{k}\Phi (\mathbf {x} _{i})\right)^{T}\Phi (\mathbf {x} )}$

Nous notons que ${\displaystyle \Phi (\mathbf {x} _{i})^{T}\Phi (\mathbf {x} )}$ désigne le produit scalaire, qui correspond simplement aux éléments de la matrice noyau ${\displaystyle K}$. Il ne reste alors plus qu'à calculer et normaliser le ${\displaystyle \mathbf {a} _{i}^{k}$, ce qui peut être fait en trouvant vecteur propre :

${\displaystyle N\lambda \mathbf {a} =K\mathbf {a} }$

où ${\displaystyle N}$ est le nombre de points de données dans l'ensemble, et ${\displaystyle \lambda }$ et ${\displaystyle \mathbf {a} }$ sont les valeurs propres et les vecteurs propres de ${\displaystyle K}$. Ensuite, pour normaliser les vecteurs propres ${\displaystyle \mathbf {a} ^{k}$, nous exigeons que

${\displaystyle 1=(V^{k})^{T}V^{k}$

Il faut être prudent quant au fait que, peu importe si ${\displaystyle x}$ a une moyenne nulle ou non dans son espace d'origine, il n'est pas garanti qu'il soit centré dans l'espace de re-description (que nous ne calculons jamais explicitement). Étant donné que des données centrées sont nécessaires pour effectuer une analyse des composantes principales efficace, nous « centralisons » ${\displaystyle K}$ pour devenir ${\displaystyle K'}$

${\displaystyle K'=K-\mathbf {1_{N} K-K\mathbf {1_{N} +\mathbf {1_{N} K\mathbf {1_{N} }$

où ${\displaystyle \mathbf {1_{N} }$ désigne une matrice N x N pour laquelle chaque élément prend une valeur ${\displaystyle 1/N}$ . Nous utilisons ${\displaystyle K'}$ pour exécuter l'algorithme d'ACP à noyau décrit ci-dessus.

Une autre mise en garde concernant l'ACP à noyau est importante. Dans l'ACP linéaire, nous pouvons utiliser les valeurs propres pour classer les vecteurs propres en fonction de la part de variation des données capturée par chacune des composantes principales. Ceci est utile pour la réduction de la dimensionnalité des données et pourrait également être appliqué à la KPCA. Cependant, en pratique, il existe des cas où toutes les variations des données sont les mêmes. Cela est généralement dû à un mauvais choix du paramètre d'échelle du noyau.

En pratique, une grande base de données conduit à un grand K, et le stockage de K peut devenir un problème. Une façon de résoudre ce problème est d’effectuer un partitionnement de données et de remplir le noyau avec les moyennes de ces clusters. Étant donné que même cette méthode peut produire un K relativement grand, il est courant de calculer uniquement les P valeurs propres les plus grandes.

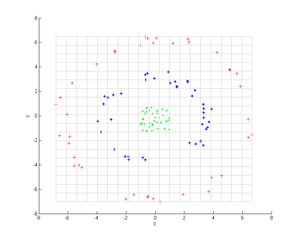
Considérons trois nuages de points concentriques (comme illustrés); nous souhaitons utiliser l'ACP à noyau pour identifier ces groupes. La couleur des points ne représente pas les informations impliquées dans l'algorithme, mais montre uniquement comment la transformation déplace les points de données.

Tout d’abord, considérons le noyau

${\displaystyle k({\boldsymbol {x},{\boldsymbol {y})=({\boldsymbol {x}^{\mathrm {T} }{\boldsymbol {y}+1)^{2}$

En appliquant ceci à l'ACP à noyau, on obtient l’image suivante.

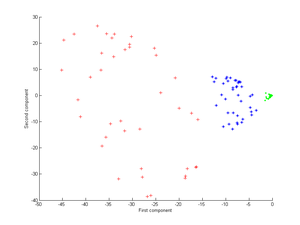
Considérons maintenant un noyau gaussien :

${\displaystyle k({\boldsymbol {x},{\boldsymbol {y})=e^{\frac {-||{\boldsymbol {x}-{\boldsymbol {y}||^{2}{2\sigma ^{2},}$

Ca noyau est une mesure de proximité, égale à 1 lorsque les points coïncident et égale à 0 à l'infini.

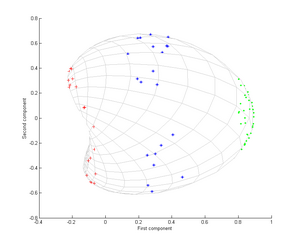
Notons en particulier que la première composante principale suffit à distinguer les trois groupes différents, ce qui est impossible en utilisant uniquement une ACP linéaire, car l'ACP linéaire ne fonctionne que dans l'espace donné (dans ce cas bidimensionnel), dans lequel ces nuages de points concentriques ne sont pas linéairement séparables.

Il a été démontré que l'ACP à noyau est utile pour la détection des nouveautés^[2] et la suppression du bruit dans les images

• Partitionnement de données
• Partitionnement spectral
• Analyse canonique à noyaux

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kernel principal component analysis » (voir la liste des auteurs).

• Portail des probabilités et de la statistique
• Portail de l’informatique
• Portail de l'informatique théorique
• Portail de l’intelligence artificielle
• Portail des données