Intégration (mathématiques)
En mathématiques, l'intégration ou calcul intégral est l'une des deux branches du calcul infinitésimal, l'autre étant le calcul différentiel.
Les intégrales sont utilisées dans de multiples disciplines scientifiques notamment en physique pour des opérations de mesure de grandeurs (longueur d'une courbe, aire, volume, flux) ou en probabilités. Ses utilités pluridisciplinaires en font un outil scientifique fondamental[1]. C'est la raison pour laquelle l'intégration est souvent abordée dès l'enseignement secondaire.
Le concept d'intégrale a été raffiné depuis son introduction au XVIIe siècle par Leibniz et Newton, permettant ainsi de les calculer pour des fonctions de moins en moins régulières. On rencontre ainsi aujourd'hui les intégrales dites de Riemann, de Lebesgue ou de Kurzweil-Henstock. Mais toutes ces définitions coïncident dans le cas des fonctions continues sur un segment.
Le symbole mathématique représentant l'intégration, le « S long » : , est appelé signe somme, signe d'intégration, signe intégral ou intégrateur ; il a été introduit par Leibniz pour noter l'intégrale.

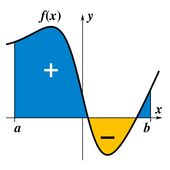
(1) la courbe représentative de la fonction f (d'équation ),
(2) l'axe des abscisses
et (3-4) les droites verticales d'abscisses a et b.
Le présent article décrit l'intégrale de fonctions de la variable réelle. Pour les extensions aux fonctions de plusieurs variables, voir les articles Intégrale curviligne, Intégrale multiple et Intégrale de surface. Le cas général de l'intégrale des fonctions définies sur un espace mesurable muni d'une mesure positive est traité dans l'article Intégrale de Lebesgue. Une autre extension est l'intégrale des formes différentielles.
Cas particulier de la fonction continue sur un intervalle fermé [a, b]
Calcul d'aire

Dans un plan muni d'un repère cartésien, on choisit comme unité d'aire l'aire du quadrilatère OIKJ où O est l'origine du repère et I, J et K les points de coordonnées respectives (1 ; 0), (0 ; 1) et (1 ; 1).
Si f est une fonction réelle positive continue prenant ses valeurs dans un segment I = [a, b], alors l'intégrale de f sur I, notée
est l'aire d'une surface délimitée par la représentation graphique de f et par les trois droites d'équation x = a, x = b, y = 0, surface notée Sf. (Voir schéma ci-contre pour l'intervalle I = [0, a].)

On donne un signe positif à l'aire des surfaces comme Sf situées au-dessus de l'axe des abscisses. Pour pouvoir traiter aussi les fonctions négatives, on donne un signe négatif aux portions situées sous cet axe.
Ainsi, pour définir l'intégrale d'une fonction continue dans le cas général (positive ou négative), il suffit de définir f + et f –, communément appelées parties positive et négative de f respectivement, comme suit :
puis de définir l'intégrale de f à partir de f + et f –, fonctions continues et positives :
Plus précisément, définir l'aire de cette surface consiste, dans la définition de la théorie de Riemann, à approcher f par une suite de fonctions gn dont on connaît l'intégrale (en général : des rectangles qu'on définit d'aire ± longueur × largeur) et telle que la différence entre f et gn tende vers 0 quand n tend vers l'infini.
Avec cette méthode, il est possible de définir l'« aire sous la courbe » d'une fonction bornée ne présentant qu'un ensemble dénombrable de points de discontinuité.
On appelle f un intégrande[2], et on note ∫ (un s allongé, mis pour somme) l'opérateur mathématique, appelé intégrateur, qui est associé à l'intégration. Ce symbole est un ancien s long : en effet, Leibniz s'est servi de l'initiale du mot latin summa, « somme », lequel était le plus souvent écrit ſumma. À la différence du s long, ∫, en typographie, garde toujours une hampe descendant au-dessous de la ligne de base, en romaine comme en italique. (Voir l'article Notation de Leibniz pour une justification de la notation complète, et en particulier du symbole dx.).
Lien avec les primitives
Le but du calcul intégral est de développer des méthodes permettant de calculer les intégrales. La principale méthode pour calculer une intégrale passe par la notion de primitive d'une fonction. La « primitivation » est l'opération qui, à partir d'une fonction f, donne une fonction F dérivable et dont la dérivée est égale à f : F′(x) = f(x).
On montre que toute fonction continue sur un segment [a, b] admet des primitives, et que l'intégrale de a à b est égale à F(b) – F(a), indépendamment de la primitive choisie.
De plus, l'ensemble des primitives d'une fonction f continue sur un intervalle I est donné par l'ensemble de ses intégrales indéfinies
où a est un point de I et K un réel quelconque.
Le théorème fondamental de l'analyse affirme que les deux approches de l'intégrale (« aire sous une courbe » et « primitivation »), sont sous certaines conditions les mêmes. Ces conditions peuvent varier selon le type d'intégrale considéré. Ainsi, les fonctions qui admettent des primitives presque partout, sont aussi intégrables au sens de Kurzweil-Henstock, mais pas nécessairement au sens de Riemann ou au sens de Lebesgue.
Historique
L'histoire des mathématiques doit beaucoup à la théorie de l'intégration, et sa place prédominante a façonné l'analyse en offrant à qui une solution, à qui un problème. Le lustre des « méthodes intégrales » en Grèce antique l'atteste (voir méthode d'exhaustion), et bien qu'il faille attendre le calcul infinitésimal pour une première formalisation, elles nous avaient déjà offert de profonds et beaux résultats : les Athéniens évaluèrent les grandeurs de l'espace puis en démontrèrent implicitement l'existence et l'unicité ; au XVIIe siècle naissent des méthodes générales de « calcul de l'infini » (rectification de courbes, quadratures, etc.) C'est alors que la méthode des indivisibles de Cavalieri voit le jour.
C'est Leibniz qui introduit le fondement de la théorie de l'intégration (Geometria recondita, 1686[3].), qu'il conçoit comme opération inverse de la différentiation (Nova methodus pro maximis et minimis, 1684), d'une part par un symbolisme inégalé reliant intégration et dérivation, d'autre part par la mise en place des principaux théorèmes perpétués jusqu'à aujourd'hui.
La formalisation de cette théorie a revêtu diverses formes. Elle aboutit tardivement, à cause de la complexité des problèmes soulevés :
- que sont les fonctions ? les réels ? (ces questions ne furent pleinement élucidées que grâce au développement de l'analyse au XIXe siècle) ;
- quelles fonctions peuvent s'intégrer ? (c'est la question de l'intégrabilité ; elle est liée, entre autres, à des problèmes de convergence).
L'intégrale de Riemann (Bernhard Riemann, 1854, publication posthume en 1867) puis l'intégrale de Lebesgue (Henri-Léon Lebesgue, 1902) ont marqué les esprits par leur formalisation aboutie. L'intégration est encore un sujet pour la recherche contemporaine ; en témoignent des extensions telles que l'intégrale d'Itō, l'intégrale de Kurzweil-Henstock, ou la récente construction de Bongiorno (1996)[4].
Extension de l'intégrale aux fonctions non continues sur un intervalle
Différences entre l'intégration au sens de Riemann et au sens de Lebesgue
Le schéma général utilisé pour construire une intégrale et qui cherche à mesurer l'aire du domaine sous la courbe est le même pour les trois approches de l'intégration :
- au sens de Riemann, voir Intégrale de Riemann
- au sens de Lebesgue, voir Intégrale de Lebesgue
- ou au sens de Kurzweil-Henstock, voir Intégrale de Kurzweil-Henstock.
D'abord, on considère une famille de fonctions élémentaires, pour lesquelles nous avons un moyen évident de mesurer l'aire sous la courbe. Dans le cas de l'intégrale de Riemann ou de Kurzweil-Henstock, ce sont les fonctions en escalier dont l'aire sous la courbe est égale à la somme des aires des rectangles ; les fonctions en escalier étant constantes sur des intervalles, le domaine sous la courbe d'une telle fonction peut alors être vu comme une réunion de rectangles. Pour l'intégrale de Lebesgue, les fonctions élémentaires sont les fonctions étagées, constantes, non plus sur des intervalles, mais sur des parties mesurables (approche plus souple et plus générale).
L'intégrale de Riemann permet d'intégrer entre autres les fonctions croissantes ou décroissantes, et les fonctions continues, donc aussi les fonctions continues par morceaux, ainsi que les fonctions monotones par morceaux. Toute limite uniforme d'une suite de fonctions intégrables au sens de Riemann est intégrable au sens de Riemann. Cependant une limite simple (c'est-à-dire que f(x) = lim fn(x) pour tout x de l'intervalle [a, b] sans condition d'uniformité en x) de fonctions Riemann intégrables n'est pas nécessairement Riemann intégrable. Il est possible de caractériser les fonctions intégrables au sens de Riemann : ce sont les fonctions bornées dont l'ensemble des points de discontinuité est de mesure nulle (critère de Lebesgue).
L'intégration au sens de Lebesgue permet d'intégrer plus de fonctions (dont des fonctions qui ne sont même pas localement bornées), et elle donne la même valeur à l'intégrale lorsque la fonction est déjà intégrable au sens de Riemann. Elle a l'avantage de munir l'espace vectoriel des fonctions intégrables (modulo l'égalité presque partout) d'une structure d'espace normé complet. Ceci est essentiel pour beaucoup d'applications. Cependant, on perd la notion de sommes de Riemann, et il existe des contextes (étude des suites uniformément distribuées par exemple) où les fonctions intégrables au sens de Riemann surviennent naturellement ; pour une généralisation de cette dernière permettant néanmoins d'intégrer également toutes les fonctions mesurables (au sens de Lebesgue), voir l'intégrale de Kurzweil-Henstock.
Cas des fonctions monotones
Si sur le segment (ainsi Sf est inclus dans Sg), alors nous aurons
Si l'on suppose par exemple la fonction f monotone sur [a, b], il est possible d'approcher son aire en utilisant soigneusement une fonction élémentaire s (dans le cas de l'intégration de Riemann ou de Kurzweil-Henstock, une fonction en escalier, et dans le cas de l'intégration de Lebesgue, une fonction étagée). Nous choisissons s telle que s ≤ f mais en supposant s très proche de f, au sens où, ayant préalablement fixé un ε > 0 arbitrairement petit, les valeurs prises par f s'éloignent de celles prises par s d'au plus ε, ce qui se note .
L'aire sous s, facilement calculable comme somme d'aires de rectangles, est majorée par l'intégrale de f, et est appelée somme inférieure.
Cas des fonctions non monotones
Dans le cas de l'intégrale de Riemann ou de Kurzweil-Henstock, nous fabriquons aussi des sommes supérieures de la même façon : nous choisissons une fonction en escalier, disons σ, telle que σ ≥ f en supposant σ de la même manière très proche de f, et nous considérons une somme supérieure comme un majorant de l'aire du domaine sous f. Dans le cas de l'intégrale de Riemann, les rectangles utilisés ont des bases de longueur majorée par une constante ; dans le cas de l'intégrale de Kurzweil-Henstock, les rectangles ont des bases de longueur variable. La théorie de Lebesgue n'utilise pas de sommes supérieures.
On montre que l'ensemble des aires sous les fonctions s que l'on peut choisir (respectivement sous les fonctions σ dans la théorie de Riemann ou de Kurzweil-Henstock), admet une borne supérieure (resp. inférieure, et c'est la même). Cette valeur est alors appelée intégrale de f sur [a, b].
Les fonctions que nous pouvons intégrer sont appelées fonctions intégrables.
Cependant, les différences commencent ici ; la théorie de Riemann est de loin la plus simple, mais de cette simplicité résulte que l'ensemble des fonctions intégrables est plus restreint que celui de la théorie de Lebesgue ou de Kurzweil-Henstock. En plus, l'interaction entre les limites et l'intégrale sont plus difficiles à décrire dans la théorie de Riemann.
Généralisation à un intervalle quelconque
Fonctions intégrables positives
La généralisation de l'intégrale à un intervalle quelconque se fait en se basant sur la notion d'intégrale définie sur un segment.
Soit f une fonction à valeurs réelles positives, continue définie sur un intervalle I quelconque, noté (a, b), où a est réel ou égal à –∞ et b est réel ou égal à +∞, et où les parenthèses signifient [ ou ] (avec exclusion si valeur infinie).
On dit que f est intégrable sur l'intervalle I lorsque l'ensemble est majoré. Partie non vide et majorée de ℝ, il admet une borne supérieure : on la note alors et on l'appelle intégrale de f sur I.
Avec ces mêmes données, on a l'équivalence logique : f intégrable sur ]a, b[ si et seulement si toute primitive de f sur ]a, b[ admet une limite finie en a et en b.
Dans le cas où une fonction f est intégrable sur un intervalle ]a, b[, on a
Fonctions intégrables à valeurs complexes ou vectorielles
Enfin, pour une fonction continue définie sur un intervalle I quelconque et à valeurs dans ℂ, on pose par définition : f est intégrable sur I si |f| intégrable sur I en tant que fonction à valeurs réelles positives.
De même pour f continue définie sur I et à valeurs dans un espace vectoriel normé (E,║.║), f est intégrable sur I si et seulement si ║f║ est intégrable sur I en tant que fonction à valeurs réelles positives.
Intégrales impropres
Il se peut très bien que « l'aire sous la courbe » d'une fonction définie et continue sur I et à valeurs réelles (changeant de signe) ait une limite en faisant tendre les extrémités d'une suite de segments inclus dans I vers les bornes de I, sans toutefois que la fonction en jeu soit intégrable sur I au sens de la définition. On parle alors d'intégrale semi-convergente, la valeur de l'aire trouvée est appelée intégrale impropre. C'est le cas avec l'exemple classique de la fonction de ]0,+∞[ dans ℝ qui à tout t > 0 associe (sin t)/t : elle peut être prolongée continûment par 1 en zéro mais le problème de l'intégrabilité se pose au voisinage de +∞. On peut calculer son intégrale impropre (puisqu'elle n'est que semi-convergente) : on trouve :.
Moyenne
Valeur moyenne d'une fonction
Pour toute fonction continue (ou même seulement continue par morceaux) sur un segment [a, b] tel que a < b, la valeur moyenne de f sur [a, b] est le réel m défini par :
Cette notion généralise celle de moyenne d'un nombre fini de réels en l'appliquant à un nombre infini de valeurs prises par une fonction intégrable. Elle sert par exemple dans la décomposition en série de Fourier d'une fonction périodique : c'est la composante constante. En traitement du signal, pour les signaux périodiques, il s'agit de la composante continue (offset).
Moyennes pondérées
On peut aussi, par analogie avec les moyennes pondérées d'un nombre fini de réels, affecter « à chacune des valeurs prises par la fonction » un coefficient strictement positif. On utilise alors ce que l'on appelle une fonction poids ( pour l'initiale de weight, poids en anglais) :
Ce procédé peut aussi s'utiliser sur un intervalle ouvert ou semi-ouvert mais borné (c'est-à-dire fini) où la fonction f.w est intégrable. On peut citer l'exemple classique servant à montrer l'orthogonalité de la famille des polynômes de Tchebychev :
où la fonction Tn×Tp est continue sur le fermé [0, 1] et où la fonction poids est
Son intégrale est bien définie et vaut .
Propriétés des intégrales
Relation de Chasles
Soient f une fonction continue sur I et a, b et c trois réels de I.
Linéarité
Soient f et g deux fonctions continues sur I et a, b deux réels de I.
- (linéarité de la fonction intégrale)
Inégalités
Soient f et g deux fonctions continues sur I et a, b deux réels de I.
- Si f(x) ≤ g(x) sur [a, b], alors
- Inégalité de la moyenne. Si f est continue sur [a, b], avec a ≤ b et si pour tout x de cet intervalle, on a :
alors
Intégration par parties
Soient u et v deux fonctions de classe C1 (i. e. dérivables de dérivées continues sur le segment [a, b]) :
Intégration par changement de variable
Soit f une fonction numérique continue, et φ une fonction de classe C1 sur [a, b] dont l'image est contenue dans le domaine de définition de f. Alors :
Parmi les multiples exemples, on retient trois changements de variables simples connus sous les noms de « formule du roi », « formule de la reine » et « formule du valet », qui permettent d'exploiter les propriétés de symétrie ou de périodicité des intégrandes et de simplifier les calculs[5]:
- Formule du roi
Pour une intégrale définie sur un intervalle , le changement de variables donne :
- Formule de la reine
Pour une intégrale définie sur un intervalle , le changement de variables , combiné à la relation de Chasles, donne :
- Formule du valet
Pour une intégrale définie d'une fonction T-périodique sur un intervalle , le changement de variables sur chaque intervalle , combiné à la relation de Chasles, donne :
Calcul d'intégrales sous forme explicite
Les formules précédentes, bien que permettant la détermination de nombreuses intégrales et primitives, ne permettent pas d'obtenir explicitement la plupart d'entre elles. Plus précisément, des théorèmes comme celui de Liouville montrent qu'il est par exemple impossible d'exprimer les primitives d'une fonction telle que à l'aide des fonctions usuelles (dites élémentaires), ce qui oblige à en définir de nouvelles (ici, la fonction logarithme intégral)[a] ; de même, la plupart des intégrales définies ne peuvent être calculées sans introduire de nouvelles constantes (voir l'article Algèbre des périodes).
Calcul numérique d'une intégrale


On ne connaît pas toujours une formule pour décrire une fonction, par exemple dans le cas d'une courbe expérimentale. Dans d'autres cas, on ne connaît pas de méthode analytique pour exprimer la primitive, ou bien on n'a pas besoin de l'expression analytique et seule la valeur numérique suffit. On a recours dans ces cas-là à une méthode numérique.
Les méthodes numériques consistent à prendre une suite de valeurs (xi, f(xi)), les valeurs des xi étant si possible équidistantes : xi+1 – xi = p. On peut ensuite appliquer différentes méthodes, dont les deux principales consistent à faire la somme d'aires Si :
- méthode des rectangles : Si est l'aire d'un rectangle de hauteur f(xi) et de largeur p, on prend donc pour approximation
- ;
- méthode des trapèzes : Si est l'aire d'un trapèze de bases f(xi) et f(xi+1), et de hauteur p (graphiquement, c'est plutôt sa « largeur »), on prend donc pour approximation
Les méthodes numériques sont automatisables sur les ordinateurs et calculatrices programmables.
D'autres méthodes sont possibles.
Méthode graphique de tracé d'une primitive


On peut utiliser des méthodes graphiques utilisant le fait que la valeur de la fonction en un point est la pente de la primitive.
Considérant le même découpage que précédemment, on découpe l'intervalle d'intégration en bandes verticales de largeur p centrées sur les valeurs xi. Sur un graphique voisin, le graphique polaire, on place des vecteurs à l'origine O et l'on considère un point P sur l'axe des x, distant de O ; P est appelé le pôle. Si l'on relie P aux extrémités des vecteurs, on obtient des droites di dites polaires, dont les coefficients directeurs ai sont proportionnels aux valeurs de f(xi ) :
On reporte ensuite les directions de ces droites polaires pour former un polygone funiculaire. L'axe des ordonnées est à une échelle 1/OP. L'ordonnée de départ du funiculaire correspond à la constante d'intégration.
Si, au lieu de placer l'origine des vecteurs en O, on les met bout à bout, on effectue alors une double intégration, puisque les valeurs sont cumulées. Le pôle n'est plus nécessairement sur l'axe des x ; cela incline différemment la courbe obtenue, et correspond à la constante d'intégration de la première intégrale. Ceci est par exemple appliqué pour déterminer le diagramme des moments fléchissants d'une poutre en flexion à partir des charges, ou bien la forme de cette poutre à partir du diagramme des moments fléchissants.
Méthodes analogiques
Mesure de surface
Il est possible d'estimer la valeur d'une intégrale par des mesures physiques. Par exemple, on trace la courbe sur une feuille de papier, on découpe la feuille suivant le tracé puis on pèse le résultat. En effet, si la masse surfacique est uniforme, alors le poids mesuré est proportionnel à l'aire. Ce principe était notamment utilisé pour déterminer l'aire d'un pic dans des mesures, par exemple pour faire de l'analyse quantitative par diffractométrie X.
Intégration d'une fonction d'intensité électrique
On peut utiliser d'autres phénomènes physiques « intégrateurs », comme le chauffage d'un corps :
- la fonction à intégrer est représentée par un courant d'intensité variable qui passe dans un résisteur chauffant ;
- l'intégrale est représentée par la température du corps chauffé, par exemple une quantité donnée d'huile ;
puisque la variation de température dT est reliée à la chaleur reçue δQ par l'équation :
- où m est la masse d'huile et Cp sa capacité thermique massique.
Cette variation dT est donc proportionnelle à l'intensité i par la loi d'Ohm :
- , où dt est la durée de chauffage,
soit
Calculateurs analogiques électroniques
Anecdotes
En 1994, une chercheuse en médecine a réinventé sans le savoir la méthode d'intégration par la méthode des trapèzes en cherchant à proposer une méthode de calcul pour mesurer la réponse biologique à la prise de glucose chez le patient diabétique[6]. Si le fait de redécouvrir un résultat ou une méthode existante n'est pas rare en sciences, le calcul intégral est censément bien connu des étudiants de premier cycle scientifique, ce qui confère une dimension cocasse involontaire à cet article[7]. En octobre de la même année, des contributions publiées dans la même revue relevaient d'ailleurs cet état de fait[8],[9].
Notes et références
Notes
- Historiquement, c'était déjà le cas de la fonction (logarithme naturel), aujourd'hui considérée comme une fonction usuelle mais définie comme une certaine intégrale de la fonction , qu'on ne peut pas exprimer explicitement à l'aide des fonctions élémentaires antérieurement connues.
Références
- Alain Michel, Constitution de la théorie de l'intégration, p. 10, aperçu sur Google Livres.
- Mot masculin, comme multiplicande, opérande, radicande.
- Gottfried Wilhelm Leibniz : De geometria recondita et analysi indivisibilium atque infinitorum (Calcul intégtral : De la géométrie profonde et analyse des indivisibles et de l'infini), en latin dans les Acta Eruditorum, Leipzig, 1686 (lire en ligne). Traduction française par Marc Parmentier, La naissance du calcul différentiel : 26 articles des Acta Eruditorum, Paris, Vrin, 1995, p. 126 (aperçu en ligne).
- (it) B. Bongiorno, « Un nuovo integrale per il problema delle primitive », Le Matematiche, vol. 51, no 2, , p. 299-313 (lire en ligne).
- (en) Amit M. Agarwal, Skills in Mathematics - Integral Calculus for JEE Main and Advanced (lire en ligne)
- (en) Mary M Tai, « A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves », Diabetes Care, vol. 17, no 2, , p. 152–154 (ISSN 0149-5992 et 1935-5548, DOI 10.2337/diacare.17.2.152, lire en ligne, consulté le )
- (en) « Medical researcher discovers integration, gets 75 citations », sur An American Physics Student in England, (consulté le )
- (en) Thomas M. S. Wolever, « Comments on Tai's Mathematic Model », Diabetes Care, vol. 17, no 10, , p. 1223-1224 (lire en ligne)
- (en) Jane Monaco et Randy Anderson, « Tai's Formula Is the Trapezoidal Rule », Diabetes Care, vol. 17, no 10, , p. 1224-1225 (lire en ligne)
Voir aussi
Articles connexes
Bibliographie
- Jean-Yves Briend, Petit traité d'intégration, EDP Sciences, 2014, aperçu sur Google Livres
- Marc Briane et Gilles Pagès, Théorie de l’intégration - Convolution et transformée de Fourier, Vuibert, 2012
- Frédéric Riesz, « L'évolution de la notion d'intégrale depuis Lebesgue », Annales de l'Institut Fourier, vol. 1, , p. 29-42 (lire en ligne)
Liens externes
- Ressource relative à l'audiovisuel :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Éric Charpentier, Textes de la journée sur l'intégration, Université Bordeaux I,
- « Les différentes techniques d'intégration et de calcul de primitives », sur gecif.net — Nombreux exemples détaillés.
- Jean Gounon, « Intégrale de Riemann et Intégrale de Lebesgue », sur dma.ens.fr/culturemath — Une présentation systématique de deux théories de l'intégration pour les fonctions réelles d'une variable réelle, en 9 pages, le plus souvent sans démonstration.








![{\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a)=\left[F(x)\right]_{a}^{b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09c2e902eeedc72f8a966da8a79b8637a7b4188c)

![{\displaystyle [a,b],\ 0\leqslant f\leqslant g}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09be8ae79e1b1f84a6d2c97f928b49811834b3f9)

![{\displaystyle \|f-s\|_{\infty }=\sup _{[a,b]}\,|f-s|\leq \varepsilon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cafcc2a690b76602ce7ce70902914ce5829d8a)
![{\displaystyle \textstyle \{\int _{[c,d]}f~|~[c,d]\subset I\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe37710e4e1a96e7a96386514495f33fcb381ae6)

![{\displaystyle \int _{]a,b[}f=\lim _{b}F-\lim _{a}F.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b2b2090c7ff0d04c4976628d5feea5b60e33e7e)
















![{\displaystyle \int _{a}^{b}u(x)v'(x)\,\mathrm {d} x=[u(x)v(x)]_{a}^{b}-\int _{a}^{b}u'(x)v(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ed93b88211b1ffa97d18c59f597625232fcff9f)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle [0,2a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b08e3fcbf44ed1c0caf67e303174216e621c27d)

![{\displaystyle \int _{0}^{2a}f(t)\,\mathrm {d} t=\int _{0}^{a}\left[f(x)+f(2a-x)\right]\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f050d5b16cf9bbda8880b0ba37ddb3ea3832b01)
![{\displaystyle [0,nT]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91791dfc3e2384d757440824d2f355966496456b)

![{\displaystyle [kT,(k+1)T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6661f5b0d64025affeb0a4439a2ff7fedc4c0f2e)










