Compression par ondelettes
La compression par ondelettes est une technique de compression de données, bien adaptée à la compression d'images.
Introduction aux ondelettes
Grande rivale de la DCT, la technique de compression à base d’ondelettes offre une plus grande finesse au niveau de l’analyse du signal et permet de mieux s’adapter aux propriétés locales de l’image. Il s’agit d’une voie de recherche assez prometteuse. Les codeurs JPEG 2000 et SPIHT utilisent tous deux une transformée en ondelettes dans leur schéma de compression. En revanche, seul JPEG 2000 est une norme. La compression en ondelettes étant elle-même sans pertes, c'est l'introduction facultative d'une quantification ou d'un seuillage qui entraine la perte irréversible d'informations.
La première transformation par ondelettes est une technique inventée par Alfréd Haar en 1909, avec l'ondelette du même nom. De manière assez indépendante, les ondelettes sont utilisées sporadiquement pendant le XXe siècle. En 1984, Jean Morlet, un ingénieur français, les utilise pour la prospection pétrolière et introduit le terme même d'ondelette qui fut traduit en anglais par wavelet, à partir des termes wave (onde) et le diminutif let (petite). Yves Meyer[1] (prix Abel 2017), reconnu comme un des fondateurs de la théorie des ondelettes, rassembla en 1986 toutes les découvertes précédentes (il en dénombra 16) puis définit les ondelettes orthogonales. La même année, Stéphane Mallat fit le lien entre les ondelettes et l'analyse multirésolution. Enfin, Ingrid Daubechies mit au point en 1987 des ondelettes orthogonales appelées ondelettes de Daubechies, faciles à mettre en œuvre, et utilisées dans le standard JPEG 2000.
L'utilisation de cette transformation en imagerie consiste à décomposer une image en une myriade de sous-bandes, c’est-à-dire des images de résolution inférieure. La transformation en ondelettes provient d'une analyse multirésolution de l'image. On considère des espaces d'approximations de plus en plus grossiers notés et des espaces "capturant" les détails perdus entre chaque niveau d'approximation notés avec . Les bases ondelettes se situent sur les , c'est là qu'est le cœur de la compression sans perte.
Les coefficients d'ondelettes dans les mettent en évidence des informations sur les contours, les textures, leur localisation et leur orientation. Le choix de l’ondelette mère est très important et fait toujours l’objet d’expérimentations pour adapter l’analyse du signal image au système de perception visuelle du lecteur humain.
Algorithme ondelettes
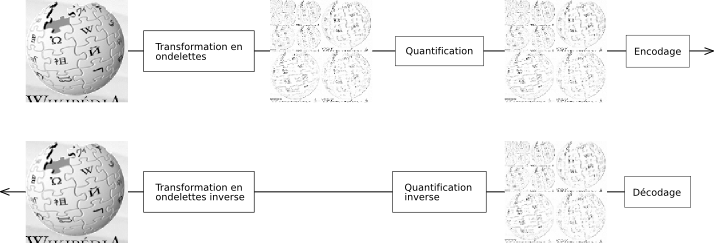
|
|---|
| Figure 1 : schéma de compression |
La compression se compose donc des étapes suivantes :
- Transformations par ondelettes.
- Quantification : les valeurs des images de détails inférieures à un certain niveau sont éliminées, en fonction de l’efficacité recherchée. C’est cette étape qui introduit des pertes.
- Codage des valeurs restantes.
Transformée ondelettes
Pour commencer, nous allons expliquer la transformée à une dimension.
Nous avons donc comme donnée originale :
Niveau 4 :
Étape après étape, nous obtenons :
Niveau 3 :
Niveau 2 :
Niveau 1 :
Nous obtenons finalement :
Niveau 0 :
Le passage d’un niveau à l’autre s’effectue, avec une ondelette de Haar, à l’aide des formules suivantes :
| Équation 1 : Transformée ondelettes |
|---|
Le premier calcul est la moyenne de deux pixels ce qui va permettre de calculer les fréquences deux fois plus basses. Le deuxième calcul est la différence entre deux pixels, ce qui correspond à l’amplitude de la fréquence à l’endroit donné. On remarque donc que la transformée DCT donne des informations sur l’amplitude des fréquences, alors que la transformée en ondelettes donne l’amplitude de la fréquence à un endroit donné. Cette dernière donne donc un rendu plus proche de la perception humaine car pour le son par exemple, on remarque s’il y a des basses ou des aigus à un instant donné. On peut également remarquer que dans le cas de la DCT, les fréquences varient de façon linéaire tandis que dans le cas de la transformée par ondelettes les fréquences varient de manière logarithmique. Ceci est également plus proche de notre perception.
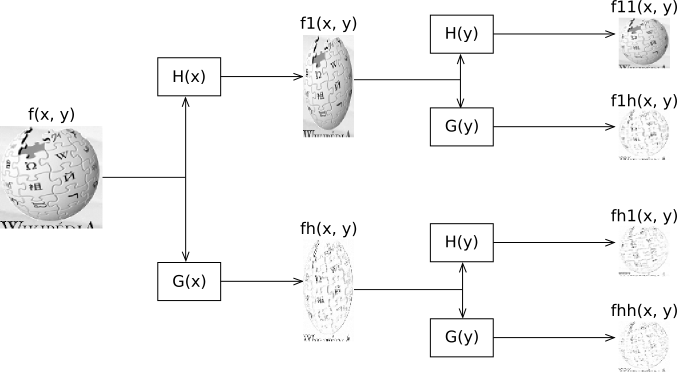
Transformée ondelettes à deux dimensions
On distingue 4 étapes différentes pour procéder à la transformation dans le cas très particulier de l'ondelette de Haar :
- Moyenner les pixels de l’image originale deux à deux suivant l’axe horizontal ; par exemple :
- Calculer l’erreur entre l’image originale et l’image sous-échantillonnées dans le sens horizontal ; par exemple :
- Pour chacune des deux images intermédiaires, moyenner les pixels deux à deux suivant l’axe vertical ; par exemple :
- Pour chacune des deux images intermédiaires, calculer l’erreur suivant l’axe vertical ; par exemple :
Ce qui donne graphiquement :

|
|---|
| Figure 2 : schéma de transformation d’un niveau à l’autre |
Le résultat est une image d’approximation qui a une résolution divisée par deux et trois images de détails qui donnent les hautes fréquences de l’image originale. Cette transformation est répétée autant de fois que nécessaire pour obtenir le nombre voulu de sous-bandes.
Niveaux après niveaux nous obtenons :
|
|---|
| Figure 3 : transformée en ondelettes niveau après niveau |
Décompression ondelettes
La transformation inverse par ondelettes reconstruit une image originale. La construction de l’image à partir des sous-bandes restitue l’image en mode progressif. L’affichage de l’image peut s’effectuer en deux modes :
- Soit la taille de l’image augmente au fur et à mesure de la lecture du fichier compressé.
- Soit la résolution de l’image augmente au fur et à mesure de la lecture du fichier compressé.
Comparaison des algorithmes
Les principaux avantages par rapport à JPEG sont :
- Le fait que l’algorithme s’adapte mieux aux propriétés locales de l’image.
- On peut atteindre des taux de compression d’environ 50 contre 15 pour JPEG tout en ayant une qualité d’image raisonnable subjective.
Applications
- Imagerie médicale
- Détection des ondes gravitationnelles[2]
- Cinéma numérique[3]
- Codage numérique[4]
- Les empreintes digitales des fichiers du FBI
- La société "Red Digital Cinéma" fabriquant des caméras Red One, Epic et Scarlet, ont développé un format de compression pour enregistrer les données "RAW" de leurs caméra, à base d'une compression par ondelettes. Le format se nomme Redcode, utilise l'extension .r3d et le taux de compression est réglable dans la caméra. L'Epic, leur caméra haut de gamme, peut utiliser des taux de compression entre 3:1 (sans pertes selon Red) à 18:1 pour des fichiers très petits.
Bibliographie
Français
- Applet recréant les fonctions ondelettes
- Les ondelettes comme fonctions de base dans le calcul des structures électroniques - Claire Chauvin (IMAG)
- Histoire de la découverte des ondelettes par Jean Morlet
- Les ondelettes, par A. Grossmann et B. Torrésani
- Une exploration des signaux en ondelettes de Stéphane Mallat.
Anglais
- Wavelets: Data Analysis, Algorithms & Theory
- Wavelets and their application - Cahier de physique de la presse polytechnique et universitaire romande de Stefan Goedecker
- Ten lectures on wavelets de Ingrid Daubechies
Notes et références
- ↑ http://smf4.emath.fr/Publications/Gazette/2011/130/smf_gazette_130_19-36.pdf
- ↑ La première détection des ondes gravitationnelles a par exemple été réalisée avec l'algorithme de Sergey Klimenko, le 14 septembre 2015, basé sur l'analyse temps-fréquence.
- ↑ La première projection de cinéma numérique en Europe a par exemple été réalisée par Philippe Binant, le 2 février 2000, avec pour le traitement de l'image l'analyse par ondelettes.
- ↑ Prix Abel 2017.













