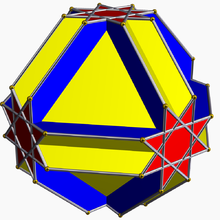
Cuboctaèdre cubitronqué

Cet article est une ébauche concernant la géométrie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Cuboctaèdre cubitronqué

Éléments

Faces	Arêtes	Sommets
20 (8{6}+6{8}+6{8/3})	72	48

Données clés

Type	Polyèdre uniforme
Références d'indexation	U16 – C52 – W79
Symbole de Wythoff	3 4 4⁄3 |
Caractéristique	-4
Groupe de symétrie	Oh
Dual	Hexaèdre tétradyakis

modifier

En géométrie, le cuboctaèdre cubitronqué est un polyèdre uniforme non-convexe, indexé sous le nom U₁₆^[1].

Les coordonnées cartésiennes des sommets d'un cuboctaèdre cubitronqué sont toutes les permutations de

${\displaystyle (\pm 1,\pm (1+{\sqrt {2}),\pm (3+2{\sqrt {2}))\,}$

Liste des polyèdres uniformes

• Portail de la géométrie