Génération de seconde harmonique
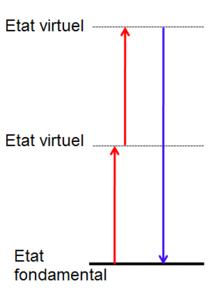
La génération de seconde harmonique (GSH ou SHG en anglais, également appelé doublage de fréquence) est un phénomène d'optique non linéaire dans lequel des photons interagissant avec un matériau non linéaire sont combinés pour former de nouveaux photons avec le double de l'énergie, donc avec le double de la fréquence ou la moitié de la longueur d'onde des photons initiaux. La génération de seconde harmonique, en tant qu'effet optique non linéaire d'ordre pair, n'est autorisée que dans les milieux sans centre d'inversion [1].
C'est un cas particulier de génération de somme de fréquence (2 photons), et plus généralement de génération d'harmonique. La génération d'harmonique moitié (en) (un cas particulier de conversion spontanée basse) est son processus inverse, où un seul photon conduit à une paire de photons ayant chacun la moitié de l'énergie incidente (et donc la moitié de la fréquence), et se produit en parallèle de la GSH, avec une probabilité plus faible cependant[2].
Ce phénomène, découvert peu après le laser à rubis, est encore très utilisé aujourd'hui pour augmenter la fréquence des lasers visibles vers l'ultraviolet ou les rayons X mous[3].
Le doublage de fréquence est également un processus de communication radio : il a été développé au début du XXe siècle et a été utilisé avec des fréquences de l'ordre du mégahertz (MHz), comme un cas particulier de multiplication de fréquence.
.
Principe
La lumière incidente sur un milieu interagit avec celui-ci. Pour les intensités usuelles, ces interactions sont dites linéaires et produisent par exemple la réfraction. Dans le cas de fortes intensités, découvertes avec la technologie du laser et les fortes puissances de crêtes qu'ils permettent d'atteindre, les effets non linéaires interviennent dès lors que l'on atteint des densités de puissance de l'ordre de 1 × 105 W cm−2[4].
La génération de seconde harmonique appartient à la classe des effets non linéaires de second ordre[5].
L'onde incidente possède une énergie qui va induire dans le matériau une polarisation . On obtient alors un champ de polarisation et une polarisation par une onde de fréquence deux fois plus grande que celle incidente[3]. L'onde de fréquence double aura une polarisation différente de celle de l'onde incidente[6].
Accord de phase
Accord critique

Une forte conversion peut être obtenue si l'accord de phase (en) est réalisé. En général, dans un cristal, les ondes fondamentales et la seconde harmonique doivent être dans des états de polarisation bien spécifiques pour interférer constructivement et permettre une génération significative. La figure ci-contre montre les trois types possibles de génération dans des milieux biréfringents.
Accord non critique
Étant donné que le processus d’accord de phase (en) signifie l’adaptation des indices optiques n à ω et 2ω, un contrôle de la température peut également être utilisé pour certains cristaux biréfringents, car n varie avec la température. Par exemple, le LBO présente un accord de phase parfait à 25 °C pour une SHG excitée à 1200 ou 1 400 nm [7], mais la température doit être élevée à 200 °C pour une SHG avec un laser à 1 064 nm. C'est accord est appelé « non critique » car il ne dépend pas de l'orientation du cristal, contrairement au cas critique.

Taux de conversion
Seulement sous certaines circonstances, le taux de conversion de photons en photons de plus haute énergie est significatif. Les deux conditions fondamentales pour une conversion efficace sont que l'intensité du faisceau pompe soit grande sur une certaine longueur de propagation et que le faisceau à convertir conserve une certaine relation de phase sur cette même longueur (on parle de condition d'accord de phase). Sous des conditions correctement optimisées, il est possible d'obtenir plus de 50 % d'efficacité de conversion (parfois même plus de 80 %) en focalisant un faisceau laser intense dans un cristal non linéaire. Cette technique est largement utilisée, notamment pour générer de la lumière verte à 532 nm à partir d'un laser Nd:YAG infrarouge à 1 064 nm. Certains pointeurs laser verts utilisent cette technique.
Tel que mentionné plus haut, une grande efficacité de conversion demande que la lumière fondamentale (à convertir) et la lumière de seconde harmonique (convertie) soient en phase. Ceci n'est pas le cas sans certaines mesures spéciales, car la vitesse de la lumière dans un matériau varie selon la longueur d'onde à cause de la dispersion de l'indice de réfraction. Dans certains cristaux non linéaires, une combinaison particulière de l'orientation du cristal et sa température fait en sorte que, à cause de la biréfringence, la lumière fondamentale et celle de seconde harmonique sont confrontés au même indice de réfraction et restent donc en phase en se propageant. Dans d'autres matériaux non linéaires, où ce phénomène n'est pas possible, on utilise une technique consistant à faire des couches de ces matériaux biréfringents avec différentes orientations pour garder les ondes approximativement en phase. Cette technique augmente grandement les possibilités de doublage de fréquence à des températures et des longueurs d'onde variées.
Diagramme de rayonnement
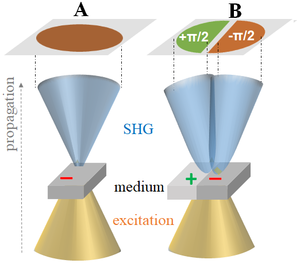
Le diagramme de rayonnement (ou patron de radiation) SHG généré avec un faisceau gaussien d'excitation a également un profil 2D gaussien (homogène) si le milieu non linéaire excité est homogène. Cependant, si le faisceau d'excitation est positionné à une interface entre deux polarités opposées (frontière +/-) parallèle à la propagation du faisceau (voir figure), le SHG sera divisé en deux lobes dont les amplitudes seront de signe opposé, c'est-à-dire déphasées de [8].
Ces interfaces sont présentes dans les sarcomères des muscles (protéine = myosine), par exemple. Notez que nous avons considéré ici que la génération vers l'avant.
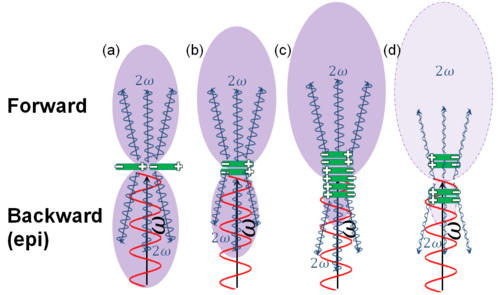
De plus, l'accord de phase (en) SHG peut également entraîner : de la SHG est également émise vers l'arrière (direction epi). Lorsque l'accord de phase (en) n'est pas respecté, comme dans les tissus biologiques, le signal vers l'arrière provient d'un désaccord de phase suffisamment élevé permettant une contribution vers l'arrière qui compense le désaccord [9]. Contrairement à la fluorescence, la cohérence spatiale du processus le contraint à n'émettre que dans ces deux directions, mais la longueur de cohérence vers arrière ((en) backward) est toujours bien plus petite que vers l'avant ((en) forward), il y a donc toujours plus de signal SHG en avant qu'en arrière [10].
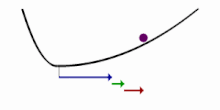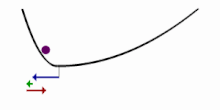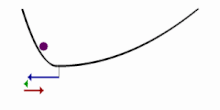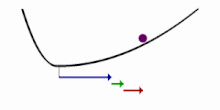
Le rapport avant (F) / arrière (B) dépend de l'arrangement des différents dipôles (en vert sur la figure) qui sont excités. Avec un seul dipôle ((a) sur la figure), F = B, mais F devient supérieur à B lorsque plusieurs dipôles sont empilés le long de la direction de propagation (b et c). Cependant, le déphasage de Gouy du faisceau gaussien impliquera un déphasage de entre les SHG générées aux extrémités du volume focal, et peut donc entraîner des interférences destructrices (signal nul) s'il y a des dipôles à ces extrémités ayant la même orientation (cas (d) sur la figure).
Utilisations commerciales
La SHG est utilisée par l’industrie pour fabriquer des lasers verts à 532 nm, doublés à partir d’une source à 1 064 nm. La lumière à 1 064 nm est dirigée sur un cristal de phosphate de monopotassium KDP. Dans les lasers à diodes de haute qualité, le cristal est revêtu à la sortie d'un filtre infrarouge pour empêcher toute fuite de lumière infrarouge (1 064 nm) intense dans le faisceau. Le proche infrarouge est invisible et ne déclenchent pas la réaction de défense de «clignement des yeux», et peut donc constituer un risque particulier. En outre, certaines lunettes de sécurité laser destinées à l'argon ou à d'autres lasers verts peuvent filtrer le composant vert à 532 nm (ce qui donne une fausse impression de sécurité), mais transmettre l'infrarouge. Ainsi, certains pointeurs lasers verts sont disponibles sur le marché, sans filtre infrarouge coûteux, souvent sans préavis du danger[11]. La SHG est également utilisée pour mesurer la largeur d’impulsions ultra-courtes dans un autocorrélateur optique (en).
Autres applications
Caractérisations d'impulsions lasers
La caractérisation d'impulsions ultra-courtes (comme la mesure de leur largeur temporelle) ne peut pas être effectuée directement avec un système uniquement électronique, car l'échelle de temps en question est inférieure à 1 ps (sec) : il faut plutôt utiliser l'impulsion elle-même, c'est pourquoi une fonction d'autocorrélation est souvent utilisée. La SHG a l’avantage de mélanger deux ondes excitatrices pour générer l’harmonique, c’est donc une bonne candidat (mais pas la seule) pour effectuer une telle mesure temporelle. L'autocorrélation optique (en), dans sa version en intensité (en) ou interférométrique ("fringe-resolved") (en) utilise la SHG [12], contrairement à l' autocorrélation d'amplitude (en). Aussi, la plupart des FROG (appelés SHG-FROG) utilisent la SHG pour mixer les deux ondes décalées dans le temps [13].
Microscopie de seconde harmonique
En imagerie biologique et médicale, la génération de seconde harmonique est utilisé pour la microscopie optique à haute résolution. Seules les structures non centrosymétriques sont capables d'émettre de la lumière SHG. Le collagène, qui se trouve dans la plupart des tissus structurels d'un vertébré, est un de ces matériaux. En utilisant un laser à impulsions courtes tel qu'un laser femtoseconde et un ensemble de filtres appropriés, la lumière d'excitation peut être facilement séparée du signal de SHG émis, car doublé en fréquence. Cela permet une résolution axiale et latérale très élevée, comparable à celle de la microscopie confocale, sans avoir à utiliser d'iris. La microscopie SHG a été utilisée pour des études sur la cornée [14] et la lame criblée de la sclère dans l'œil[15], les deux étant constitué principalement de collagène. La SHG peut être produite par plusieurs colorants organiques non centrosymétriques, cependant la plupart des colorants organiques génèrent également une fluorescence qui peut se mélanger à la SHG[16]. Jusqu'à présent, seules deux classes de colorants organiques ne produisant aucune fluorescence collatérale et fonctionnant uniquement avec la génération de seconde harmonique ont été découvertes [16],[17]. Récemment, en utilisant la fluorescence excitée à deux photons et la microscopie SHG, un groupe de chercheurs de l'Université Oxford a montré que les molécules de type porphyrine organique peuvent avoir différents moments dipolaires de transition pour la fluorescence à deux photons et la génération du second harmonique[18],[19],
La microscopie de seconde harmonique est également utilisée en science des matériaux, par exemple pour caractériser des matériaux nanostructurés[20].
Lois de conversion (ondes planes) : calculs théoriques
Intensité générée à faible conversion
On traite ici du cas idéal d'une onde plane (non réalisé en pratique, car souvent le faisceau est Gaussien) excitatrice d'amplitude E(ω) traversant un milieu non-linéaire homogène, non biréfringent, dans la direction de son vecteur d'onde k. La polarisation SHG générée à 2ω est [21]:
où est le coefficient optique non linéaire effectif qui dépend de composantes spécifiques du impliquées dans l'interaction. Avec l'approximation de la variation lente de l'enveloppe (en) et des pertes négligeables, l'équation d'onde à 2ω est :
avec .
En négligeant la déplétion de la source (voir section suivante, E(2ω) ≪ E(ω) i.e. la conversion est faible) l'amplitude reste principalement constante le long de la longueur d'interaction, . Alors, avec la condition aux limites on obtient :
En termes d'intensité optique, , donc,
Cette intensité est maximisée si l'accord de phase (en) est réalisé : Δk = 0. Sinon, la polarisation excitatrice à ω est périodiquement en accord et en désaccord de phase avec celle générée E(2ω), et la conversion reste faible en oscillant comme sin(Δkl/2). La longueur de cohérence est définie comme , au-delà de laquelle la conversion sature. Il n'est donc pas utile d'utiliser un cristal générateur plus épais que . Les cristaux d'orientation périodiquement inversée et le quasi-accord de phase (en) permettent de résoudre ce problème.
Avec déplétion


Lorsque la génération de seconde harmonique devient significative, il est nécessaire de considérer la diminution du signal fondamental. La conservation de l'énergie impose alors aux ondes du processus de vérifier les équations de Manley-Rowe (en). On a alors les équations couplées [22]:
où dénote le complexe conjugué. Pour garder une certaine simplicité, il est supposé que l'accord de phase est respecté (). Alors, la conservation de l'énergie requiert que:
où est le complexe conjugué de l'autre terme, et
- .
En considérant
on peut résoudre les équations couplées
Il vient :
En utilisant
on a
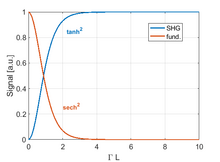
Si on suppose que est réel (pas de partie imaginaire, donc les composantes du tenseur sont en phase), on doit avoir pour assurer une bonne conversion. Alors
ou encore
où . implique aussi que
Calculs avec faisceaux gaussiens
L'onde d'excitation est supposée être un faisceau gaussien, d'amplitude :
avec , la direction de propagation, the Rayleigh range, le vecteur d'onde.
Chacune des ondes vérifie l'équation d'onde:
où .
Avec accord de phase
On peut montrer que :
(une gaussienne), est une solution de l'équation (n = 2 pour la SHG).
Sans accord de phase

Un accord de phase (en) imparfait est une condition plus réaliste dans la pratique, en particulier dans les échantillons biologiques. L'approximation paraxiale est cependant supposée toujours valable: , et pour l'harmonique, est maintenant .
Dans le cas particulier de SHG (n = 2), dans un milieu de longueur L et une position focale à , l'intensité s'écrit[23] : .
avec la vitesse de la lumière dans le vide, la permittivité du vide, l'indice optique du milieu à et le waist de l'excitation.
Ainsi, l'intensité SHG décroît rapidement dans le "bulk" (), en raison du déphasage de Gouy du faisceau gaussien.
Conformément aux expériences, le signal SHG s'annule dans la profondeur du matériau (si l'épaisseur moyenne est trop importante), et la SHG doit être générée à la surface du matériau : la conversion ne varie donc pas strictement au carré du nombre d'harmonophores, contrairement à ce que le modèle d'onde plane indique. De façon remarquable, le signal s'annule aussi pour les ordres plus élevés (comme la THG).
Matériaux utilisés pour la génération de seconde harmonique
Les matériaux capables de générer une seconde harmonique sont les cristaux sans symétrie d'inversion. Cela élimine donc l'eau, les cristaux à symétrie cubique et le verre[3].
Voici quelques matériaux non linéaires utilisés pour doubler la fréquence de la lumière fondamentale de certains lasers :
- Lumière fondamentale à 600–1 500 nm[24]: BiBO (BiB3O6)
- Lumière fondamentale à 570–4 000 nm[25] : Iodate de lithium (en) LiIO3.
- Lumière fondamentale à 800-1 100, souvent 860 ou 980 nm [26] : Niobate de potassium KNbO3
- Lumière fondamentale à 410–2 000 nm : BBO (β-BaB2O4) [27]
- Lumière fondamentale à 984–3 400 nm: KTP (KTiOPO4) ou KTA[28],
- Lumière fondamentale à 1 064 nm : phosphate de monopotassium KDP (KH2PO4), triborate de lithium (LiB3O5), CsLiB6O10 et bêta-borate de baryum BBO (β-BaB2O4).
- Lumière fondamentale à 1 319 nm : KNbO3, BBO (β-BaB2O4), phosphate de monopotassium KDP (KH2PO4), LiIO3, LiNbO3, et titanyl phosphate de potassium KTP (KTiOPO4).
- Lumière fondamentale ~1 000–2 000 nm : cristaux périodiquement orientés, comme le PPLN (niobate de lithium périodiquement polarisé)[29].
Il est à noter que des structures biologiques filamenteuses à symétrie cylindrique telles le collagène, la tubuline ou la myosine, mais aussi certains glucides (comme l'amidon ou la cellulose) sont aussi des assez bons convertisseurs de SHG (fondamental dans le proche infrarouge) [30].
Notes et références
- ↑ (en) R. Boyd, Nonlinear optics (third edition), , 2 p. (DOI 10.1016/B978-0-12-369470-6.00001-0), « The Nonlinear Optical Susceptibility »
- ↑ (en) L. Mandel et E. Wolf, Optical Coherence and Quantum Optics, , 1079 p. (DOI 10.1017/CBO9781139644105.023), « Some quantum effects in nonlinear optics »
- //books.google.com/books?id=XZxkppdiWOYC&pg=PA520
- ↑ //books.google.com/books?id=ieuR4bxA_twC&pg=PA161
- ↑ //books.google.com/books?id=-U_EnKTYWrMC&pg=PA4
- ↑ //books.google.com/books?id=-U_EnKTYWrMC&pg=PA41
- ↑ « Noncritical phase-matching », sur rp-photonics.com (consulté le )
- ↑ Laurent Moreaux, Olivier Sandre, Serge Charpak, Mireille Blanchard-Desce et Jerome Mertz, « Coherent Scattering in Multi-Harmonic Light Microscopy », Biophysical Journal, vol. 80, no 3, , p. 1568–1574 (ISSN 0006-3495, DOI 10.1016/S0006-3495(01)76129-2).
- ↑ Paul J Campagnola et Leslie M Loew, « Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms », Nature Biotechnology, vol. 21, no 11, , p. 1356–1360 (ISSN 1087-0156, DOI 10.1038/nbt894).
- ↑ Ronald LaComb, Oleg Nadiarnykh, Sallie S. Townsend et Paul J. Campagnola, « Phase matching considerations in second harmonic generation from tissues: Effects on emission directionality, conversion efficiency and observed morphology », Optics Communications, vol. 281, no 7, , p. 1823–1832 (ISSN 0030-4018, DOI 10.1016/j.optcom.2007.10.040).
- ↑ A warning about IR in green cheap green laser pointers
- ↑ Rick Trebino et Erik Zeek, Frequency-Resolved Optical Gating : The Measurement of Ultrashort Laser Pulses, Springer, , 61–99 p. (ISBN 978-1-4615-1181-6, DOI 10.1007/978-1-4615-1181-6_4, lire en ligne), « Chap4, The Autocorrelation, the Spectrum, and Phase Retrieval »
- ↑ Rick Trebino, Frequency-Resolved Optical Gating : The Measurement of Ultrashort Laser Pulses, Springer, , 61–99 p. (ISBN 978-1-4615-1181-6, DOI 10.1007/978-1-4615-1181-6_5, lire en ligne), « Chap5, FROG »
- ↑ M Han, G Giese et J Bille, « Second harmonic generation imaging of collagen fibrils in cornea and sclera », Optics Express, vol. 13, no 15, , p. 5791–7 (PMID 19498583, DOI 10.1364/OPEX.13.005791, Bibcode 2005OExpr..13.5791H, lire en ligne)
- ↑ Donald J. Brown, Naoyuki Morishige, Aneesh Neekhra, Don S. Minckler et James V. Jester, « Application of second harmonic imaging microscopy to assess structural changes in optic nerve head structure ex vivo », Journal of Biomedical Optics, vol. 12, no 2, , p. 024029 (PMID 17477744, DOI 10.1117/1.2717540, Bibcode 2007JBO....12b4029B)
- Khadria A, Fleischhauer J, Boczarow I, Wilkinson JD, Kohl MM, Anderson HL, « Porphyrin Dyes for Nonlinear Optical Imaging of Live Cells », IScience - Cell Press, vol. 4, , p. 153–163 (PMID 30240737, PMCID 6147020, DOI 10.1016/j.isci.2018.05.015)
- ↑ Nuriya M, Fukushima S, Momotake A, Shinotsuka T, Yasui M, Arai T, « Multimodal two-photon imaging using a second harmonic generation-specific dye », Nature Communications, vol. 7, , p. 11557 (PMID 27156702, PMCID 4865818, DOI 10.1038/ncomms11557, Bibcode 2016NatCo...711557N)
- ↑ Khadria A, Coene Y, Gawel P, Roche C, Clays K, Anderson HL, « Push–pull pyropheophorbides for nonlinear optical imaging », Organic and Biomolecular Chemistry, vol. 15, no 4, , p. 947–956 (PMID 28054076, DOI 10.1039/C6OB02319C)
- ↑ Reeve JE, Corbett AD, Boczarow I, Wilson T, Bayley H, Anderson HL, « Probing the Orientational Distribution of Dyes in Membranes through Multiphoton Microscopy », Biophysical Journal, vol. 103, no 5, , p. 907–917 (PMID 23009840, PMCID 3433607, DOI 10.1016/j.bpj.2012.08.003, Bibcode 2012BpJ...103..907R)
- ↑ V. K. Valev, « Characterization of nanostructured plasmonic surfaces with second harmonic generation », Langmuir, vol. 28, no 44, , p. 15454–15471 (PMID 22889193, DOI 10.1021/la302485c)
- ↑ (en) R.W. Boyd, Nonlinear Optics, 3rd edition, Boston, Academic Press, (ISBN 978-0-12-121680-1, lire en ligne)
- ↑ Frits Zernike et John E. Midwinter, Applied Nonlinear Optics, John Wiley & Sons Inc., , 197 p. (ISBN 0-486-45360-X, lire en ligne)
- ↑ Patrick Stoller, Peter M. Celliers, Karen M. Reiser et Alexander M. Rubenchik, « Quantitative second-harmonic generation microscopy in collagen », Applied Optics, vol. 42, no 25, , p. 5209 (ISSN 0003-6935, DOI 10.1364/AO.42.005209)
- ↑ « BiBO Crystals », sur newlightphotonics.com (consulté en )
- ↑ « LiIO3 crystals - Lithium Iodate Crystal », sur shalomeo.com (consulté en )
- ↑ « KNbO3 », sur laser-crylink.com (consulté en )
- ↑ « BBO Crystals », sur newlightphotonics.com (consulté en )
- ↑ « KTP Crystals », sur unitedcrystals.com (consulté en )
- ↑ J.-P. Meyn, C. Laue, R. Knappe, R. Wallenstein et M.M. Fejer, « Fabrication of periodically poled lithium tantalate for UV generation with diode lasers », Applied Physics B, vol. 73, no 2, , p. 111–114 (DOI 10.1007/s003400100623)
- ↑ (en) Francesco S. Pavone et Paul J. Campagnola, Second Harmonic Generation Imaging, CRC Taylor&Francis, , 2e éd., 476 p. (ISBN 978-1-4398-4914-9, lire en ligne)
Voir aussi
Articles connexes
- Optique non linéaire
- Génération d'harmonique moitié (en)
- Conversion spontanée basse
- Génération de fréquence optique multiple (en)
- Microscopie de seconde harmonique
- Génération de seconde harmonique de surface (en)
- Génération d'harmonique

























![{\displaystyle n_{2\omega }\left[E^{*}(2\omega ){\frac {\partial E(2\omega )}{\partial z}+c.c.\right]=-n_{\omega }\left[E(\omega ){\frac {\partial E^{*}(\omega )}{\partial z}+c.c.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4ca5d9288644f963b95e9d47a0580b409b5db3d)



![{\displaystyle {\frac {d|E(2\omega )|}{dz}=-{\frac {i\omega d_{\text{eff}{n_{\omega }c}\left[E_{0}^{2}-|E(2\omega )|^{2}\right]e^{2i\phi (\omega )-i\phi (2\omega )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6746fe4b4342d3c8c64095e5d0c490360762de7b)














![{\displaystyle \left[{\frac {\partial }{\partial {x}^{2}+{\frac {\partial }{\partial {y}^{2}+2i{k}_{1}{\frac {\partial }{\partial {z}\right]{A}(x,y,z;{k}_{1})=\left|{\begin{matrix}0{\text{ pour le fondamental}\\{\frac {\omega _{n}^{2}{c}^{2}{\chi }^{(n)}{A}(x,y,z;{k}_{1}){e}^{i\Delta kz}{\text{ pour la n-ième harmonique}\\\end{matrix}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73424d3d68d48e6eaf06e3c4ba116eaeb08d77cd)












