Ordre moyen d'une fonction arithmétique

En théorie des nombres, un ordre moyen d'une fonction arithmétique f est une fonction «simple» g approchant f en moyenne.

Plus précisément un ordre moyen de f est une fonction g réelle ou complexe, si possible continue et monotone, telle qu'on ait :

${\displaystyle \sum _{n\leqslant N}f(n)\quad {\underset {N\to +\infty }{\sim }\quad \sum _{n\leqslant N}g(n)}$

Autrement dit, les moyennes arithmétiques ou moyennes de Cesàro de f et g entre 1 et N, ou encore valeurs moyennes de f et g sont asymptotiquement équivalentes. Une telle fonction g n'est bien entendu pas unique.

Il ne faut pas confondre un équivalent asymptotique de la valeur moyenne ${\displaystyle {\frac {1}{N}{\sum _{n=1}^{N}f(n)}$ avec un ordre moyen.

Par exemple, pour ${\displaystyle f(n):=n}$, un équivalent asymptotique de la valeur moyenne, égale à ${\displaystyle (N+1)/2}$, est ${\displaystyle N/2}$, mais la fonction ${\displaystyle g(n):=n/2}$ n’est pas un ordre moyen de ${\displaystyle f}$.

Par contre, pour ${\displaystyle f(n):=\ln n}$, un équivalent de la valeur moyenne, égale à ${\displaystyle {\frac {1}{N}{\sum _{n=1}^{N}f(n)}={\frac {\ln N!}{N}$, est ${\displaystyle \ln N}$.

Dans le cas particulier où la limite $${\displaystyle \lim _{N\to \infty }{\frac {1}{N}\sum _{n\leqslant N}f(n)=c}$$

existe, on dit que ${\displaystyle f}$ possède la valeur moyenne ${\displaystyle c}$. Si de plus ${\displaystyle c\not =0}$, la fonction ${\displaystyle g(n):=c}$ est un ordre moyen de ${\displaystyle f}$.

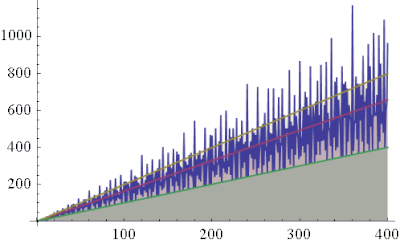
• Un ordre moyen du plus grand diviseur impair de n est 2n/3
• Un ordre moyen de d(n)^[1], nombre de diviseurs de n, est ln(n)
• Un ordre moyen de σ(n)^[2], somme des diviseurs de n, est ${\displaystyle {\frac {\pi ^{2}{6}n}$
• Un ordre moyen de φ(n)^[3], indicatrice d'Euler de n, est ${\displaystyle {\frac {6}{\pi ^{2}n}$
• Un ordre moyen de ω(n)^[4], nombre de facteurs premiers distincts de n, est ln(ln(n))
• Un ordre moyen de Ω(n)^[4], nombre de facteurs premiers de n, est ln(ln(n))
• Un ordre moyen de r(n)^[5], nombre de façon d'exprimer n comme somme de deux carrés, est π.
• Le théorème des nombres premiers équivaut au fait que la fonction de von Mangoldt Λ(n) a pour ordre moyen 1^[6], et au fait que la fonction de Möbius μ(n) a pour valeur moyenne 0^[7].

Cette notion peut être présentée à l'aide de l'exemple du nombre de diviseurs. De la formule de Dirichlet ^[8] :

${\displaystyle \sum _{n\leqslant N}{\text{d}(n)=N\ln N+(2\gamma -1)N+o(N)}$

(${\displaystyle \gamma }$ est la constante d'Euler-Mascheroni) et de la formule de Stirling :

${\displaystyle \sum _{n\leqslant N}\ln n=N\ln N-N+o(N),}$

on tire la relation asymptotique

${\displaystyle \sum _{n\leqslant N}({\text{d}(n)-(\ln n+2\gamma ))=o(N),}$

tandis que

${\displaystyle \sum _{n\leqslant N}({\text{d}(n)-\ln n)=O(N),}$

ce qui suggère que ln(n) + 2γ est un meilleur choix d'ordre moyen pour d(n) que simplement ln(n) (c'est un cas particulier de développement asymptotique).

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Average order of an arithmetic function » (voir la liste des auteurs).

• (en) G. H. Hardy et E. M. Wright, An Introduction to the Theory of Numbers (1^re éd. 1938) [détail des éditions], 6ème édition 2008, chapitres XVIII et XXII.
• G. H. Hardy et E.M. Wright (trad. François Sauvageot), Introduction à la théorie des nombres, Vuibert et Springer, 2007
• (en) Gérald Tenenbaum, Introduction to Analytic and Probabilistic Number Theory, AMS, coll. « Graduate Studies in Mathematics » (n^o 163), 2015 (ISBN 9780821898543), p. 43–65

Identités liées aux sommes de diviseurs

• Portail des mathématiques