Physique de l'imagerie par résonance magnétique

La mise en forme de cet article est à améliorer (août 2020).

La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ».

La traduction de cet article ou de cette section doit être revue (octobre 2020).

Le contenu est difficilement compréhensible vu les erreurs de traduction, qui sont peut-être dues à l'utilisation d'un logiciel de traduction automatique. Discutez des points à améliorer en page de discussion ou modifiez l'article.

La physique de l'imagerie par résonance magnétique (IRM) concerne les considérations physiques fondamentales des techniques d'IRM et les aspects technologiques des appareils d'IRM. L'IRM est une technique d'imagerie médicale principalement utilisée en radiologie et en médecine nucléaire afin d'étudier l'anatomie et la physiologie du corps et de détecter des pathologies telles que les tumeurs, l'inflammation, les affections neurologiques telles que les accidents vasculaires cérébraux (AVC), les troubles des muscles, des articulations et les anomalies du cœur et vaisseaux sanguins, entre autres. Des agents de contraste peuvent être injectés par voie intraveineuse ou dans une articulation pour améliorer l'image et faciliter le diagnostic. Contrairement à la tomodensitométrie et aux rayons X, l'IRM n'utilise aucun rayonnement ionisant et constitue donc une procédure sûre adaptée au diagnostic chez les enfants et aux analyses répétées. Les patients avec des implants métalliques non ferromagnétiques spécifiques, des implants cochléaires et des stimulateurs cardiaques de nos jours peuvent également avoir une IRM malgré les effets des champs magnétiques puissants. Cela ne s'applique pas aux appareils plus anciens, les détails destinés aux professionnels de la santé sont fournis par le fabricant de l'appareil.

Certains noyaux atomiques sont capables d'absorber et d'émettre de l'énergie radiofréquence lorsqu'ils sont placés dans un champ magnétique externe. En IRM clinique et de recherche, les atomes d'hydrogène sont le plus souvent utilisés pour générer un signal radiofréquence détectable qui est reçu par des antennes à proximité immédiate de la partie de l'organisme examiné. Les atomes d'hydrogène sont naturellement abondants chez l'homme et d'autres organismes biologiques, en particulier dans l'eau et les graisses. Pour cette raison, la plupart des IRM cartographient essentiellement l'emplacement de l'eau et des graisses dans le corps. Les impulsions des ondes radio excitent la transition d'énergie de spin nucléaire et les gradients de champ magnétique localisent le signal dans l'espace. En faisant varier les paramètres de la séquence d'impulsions, différents contrastes peuvent être générés entre les tissus sur la base des propriétés de relaxation des atomes d'hydrogène qui s'y trouvent.

Lorsqu'ils sont à l'intérieur du champ magnétique (B₀) du scanner, les moments magnétiques des protons s'alignent pour être parallèles ou antiparallèles à la direction du champ. Alors que chaque proton individuel ne peut avoir que l'un des deux alignements, la collection de protons semble se comporter comme si elle pouvait avoir n'importe quel alignement. La plupart des protons s'alignent parallèlement à B₀ car il s'agit d'un état d'énergie plus faible. Une impulsion de radiofréquence est alors appliquée, qui peut exciter des protons d'alignement parallèle à anti-parallèle, seuls ces derniers sont pertinents pour la suite. En réponse à la force qui les ramène à leur orientation d'équilibre, les protons subissent un mouvement de rotation (précession), un peu comme une roue qui tourne sous l'effet de la gravité. Les protons reviendront à l'état de basse énergie par le processus de relaxation spin-réseau. Ce processus est identifiable par un flux magnétique, qui produit une tension variable dans les bobines du récepteur pour donner le signal. La fréquence à laquelle résonne un proton ou un groupe de protons dans un voxel dépend de la force du champ magnétique local autour du proton ou du groupe de protons, un champ plus fort correspond à une différence d'énergie plus importante et des photons de fréquence plus élevée. En appliquant des champs magnétiques supplémentaires (gradients) qui varient linéairement dans l'espace, des tranches spécifiques à imager peuvent être sélectionnées, et une image est obtenue en prenant la transformation de Fourier à deux dimensions des fréquences spatiales du signal (espace réciproque). En raison de la force magnétique de Lorentz de B₀ sur le courant circulant dans les bobines, ces dernières essaieront de se déplacer produisant des sons de cognement forts, c'est pour cela que les patients ont besoin d'une protection auditive.

Histoire

Le scanner IRM a été développé de 1975 à 1977 à l'Université de Nottingham par le professeur Raymond Andrew à la suite de ses recherches sur la résonance magnétique nucléaire. Le premier scanner corporel complet a été créé en 1978^[1].

Magnétisme nucléaire

Les particules subatomiques ont la propriété du spin selon la mécanique quantique^[2]. Certains noyaux tels que ¹H (soit des protons), ²H, ³He, ²³Na ou ³¹P, ont un spin non nul et donc un moment magnétique. Dans le cas des noyaux appelés de spin-½, tel que ¹H, il y a deux états de spin, parfois appelés up en down. Les noyaux tels que ¹²C n'ont pas de neutrons ou de protons non appariés, et par conséquent pas de spin, mais cependant l'isotope ¹³C a un spin de valeur -¹⁄₂.

Lorsque ces spins sont placés dans un champ magnétique externe puissant, ils effectuent une précession autour d'un axe le long de la direction du champ. Les protons s'alignent en deux états purs d'énergie (l'effet Zeeman) : l'un à basse énergie et l'autre à haute énergie, qui sont séparés par une très petite énergie de fission.

Résonance et relaxation

La mécanique quantique est nécessaire pour modéliser avec précision le comportement d'un seul proton, cependant, la mécanique classique peut être utilisée pour décrire le comportement de l'ensemble de protons de manière adéquate. Comme pour les autres particules de spin ½, chaque fois que le spin d'un seul proton est mesuré, il ne peut avoir qu'un des deux résultats communément appelés parallèle et anti-parallèle. Pour définir l'état d'un proton ou de protons, les physiciens se réfèrent à la fonction d'onde de ce proton qui est une combinaison linéaire des états parallèle et anti-parallèle^[3].

En présence du champ magnétique B₀, les protons sembleront effectuer une précession à la fréquence de Larmor déterminée par le rapport gyromagnétique de la particule et la force du champ. Les champs statiques les plus couramment utilisés en IRM provoquent une précession qui correspond à un photon radiofréquence (RF).

La magnétisation longitudinale positive en équilibre thermodynamique est due à un minuscule excès de protons à l'état d'énergie inférieure. Cela donne une polarisation positive parallèle au champ externe. L'application d'une impulsion radiofréquence peut faire basculer ce vecteur de polarisation positif sur le côté (avec, par exemple, une impulsion dite à 90 °), ou même l'inverser (avec une impulsion dite à 180 °). Les protons entreront en phase avec l'impulsion radiofréquence et donc entre eux.

La récupération de la magnétisation longitudinale est appelée relaxation longitudinale ou relaxation T₁ et se produit de manière exponentielle avec une constante de temps T₁. La perte de cohérence de phase dans le plan transversal est appelée relaxation transversale ou relaxation T₂. T₁ est ainsi associée à l'enthalpie du système de spin, ou au nombre de noyaux à spin parallèle versus anti-parallèle. T₂ par contre est associé à l'entropie du système, ou au nombre de noyaux en phase.

Lorsque l'impulsion de radiofréquence est arrètée, la composante vectorielle transversale produit un champ magnétique oscillant qui induit un petit courant dans la bobine réceptrice. Ce signal est appelé la décroissance d'induction libre (FID en anglais). Dans une expérience de résonance magnétique nucléaire idéalisée, le FID se désintègre de manière approximativement exponentielle avec une constante de temps T₂. Cependant, en pratique il existe de petites différences dans le champ magnétique statique à différents points, phénomène nommé (« inhomogénéités ») qui font varier la fréquence de Larmor à travers le corps. Cela crée des interférences destructrices, ce qui raccourcit le FID. La constante de temps pour la décroissance observée du FID est appelée temps de relaxation T^*
₂ et est toujours inférieure à T₂. Dans le même temps, la magnétisation longitudinale commence à se rétablir de façon exponentielle avec une constante de temps T₁ qui est beaucoup plus grande que T ₂ (voir ci-dessous).

En IRM, le champ magnétique statique est augmenté par une bobine de gradient de champ pour se déplacer à travers la région balayée, de sorte que différents emplacements spatiaux deviennent associés à différentes fréquences de précession. Seules les régions où le champ est tel que les fréquences de précession correspondent à la fréquence RF subiront une excitation. Habituellement, ces gradients de champs sont modulés pour balayer la région à scanner, et c'est la variété presque infinie de séquences d'impulsions RF et de gradients qui donne à l'IRM sa polyvalence. Le changement de gradient de champ étale le signal FID dans le domaine des fréquences, mais cela peut être récupéré et mesuré par un gradient de recentrage (pour créer un prétendu « écho de gradient »), ou par une impulsion de radiofréquence (pour créer un prétendu « écho de spin) », ou en post-traitement numérique du signal propagé. L'ensemble du processus peut être répété lorsqu'une certaine relaxation T₁ s'est produite et que l'équilibre thermique des spins a été plus ou moins rétabli. Le temps de répétition (TR) est le temps entre deux excitations successives d'une même tranche^[4].

Typiquement, dans les tissus mous, T₁ est d'environ une seconde tandis que T₂ et T^*
₂ sont de quelques dizaines de millisecondes. Cependant, ces valeurs peuvent varier considérablement entre différents tissus, ainsi qu'entre différents champs magnétiques externes. Ce comportement est l'un des facteurs qui confèrent à l'IRM son formidable contraste avec les tissus mous.

Les agents de contraste IRM, tels que ceux contenant du gadolinium (III), agissent en modifiant (raccourcissant) les paramètres de relaxation, en particulier T₁ .

Imagerie

Schémas d'imagerie

Un certain nombre de schémas ont été conçus pour combiner des gradients de champ et une excitation radiofréquence pour créer une image par :

• Reconstitution 2D ou 3D à partir de projections, comme en tomodensitométrie .
• Construction d'image point par point ou ligne par ligne.
• Gradients dans le champ RF plutôt que dans le champ statique.

Bien que chacun de ces schémas soit parfois utilisé dans des applications spécialisées, la majorité des images par résonance magnétique sont aujourd'hui créées soit par la technique de transformation de Fourier bidimensionnelle (2DFT) avec sélection de tranche, soit par la technique de transformation de Fourier tridimensionnelle (3DFT). Un autre nom pour 2DFT est "spin-warp". Ce qui suit est une description de la technique 2DFT avec sélection de tranche.

La technique 3DFT est assez similaire, sauf qu'il n'y a pas de sélection de tranche et le codage de phase est effectué dans deux directions distinctes.

Imagerie de type echo-planar

Un autre schéma qui est parfois utilisé, en particulier dans le balayage du cerveau ou lorsque des images sont nécessaires très rapidement, est appelé imagerie echo-planar (EPI)^[5]: dans ce cas, chaque excitation radiofréquence est suivie d'un train d'échos de gradient avec des encodages spatiaux différents. L'EPI multiplexé est encore plus rapide, par exemple pour l'IRMf du cerveau entier ou l'IRM de diffusion^[6].

Contraste de l'image et amélioration du contraste

Le contraste de l'image est créé par des différences dans la force du signal RMN récupéré à différents endroits dans l'échantillon. Cela dépend de la densité relative des noyaux excités (généralement des protons de molécules d'eau), des différences de temps de relaxation (T₁, T₂ et T^*
₂) de ces noyaux après la séquence d'impulsions, et souvent sur d'autres paramètres discutés dans le cadre d'IRM spécialisés. Le contraste dans la plupart des images par résonance magnétique est en fait un mélange de tous ces effets, mais une conception soignée de la séquence d'impulsions d'imagerie permet d'accentuer un mécanisme de contraste tandis que les autres sont minimisés. La possibilité de choisir différents mécanismes de contraste confère à l'IRM une flexibilité considérable. Dans le cerveau, la pondération T₁ fait apparaître les connexions nerveuses de la substance blanche en blanc, les congrégations de neurones de la matière grise apparaissent grises, tandis que le liquide céphalo-rachidien apparaît sombre. Le contraste de la substance blanche, de la matière grise et du liquide céphalo-rachidien est inversé en utilisant l'imagerie T₂ ou T^*
₂, tandis que l'imagerie pondérée en densité de protons offre peu de contraste chez les sujets sains. De plus, des paramètres fonctionnels tels que le débit sanguin cérébral (CBF), le volume sanguin cérébral (CBV) ou l'oxygénation du sang peuvent affecter T₁, T₂ et T^*
₂ et peuvent donc être encodés avec des séquences d'impulsions appropriées.

Dans certaines situations, il n'est pas possible de générer un contraste d'image suffisant pour montrer de manière adéquate l'anatomie ou la pathologie concernée en ajustant les paramètres d'imagerie seuls, auquel cas un agent de contraste peut être administré. Cela peut être aussi simple que de l'eau, prise par voie orale, pour imager l'estomac et l'intestin grêle. Cependant, la plupart des agents de contraste utilisés en IRM sont sélectionnés pour leurs propriétés magnétiques spécifiques. Le plus souvent, un agent de contraste paramagnétique (généralement un composé de gadolinium ^[7],[8] ) est administré. Les tissus et fluides améliorés au gadolinium apparaissent extrêmement lumineux sur les images pondérées T₁. Ceci fournit une sensibilité élevée pour la détection des tissus vasculaires (par exemple, les tumeurs) et permet l'évaluation de la perfusion cérébrale (par exemple, en cas d'accident vasculaire cérébral). Des inquiétudes ont été soulevées récemment concernant la toxicité des agents de contraste à base de gadolinium et leur impact sur les personnes souffrant d'insuffisance rénale. (Voir les agents de sécurité et de contraste ci-dessous.)

Plus récemment, des agents de contraste superparamagnétiques, par exemple des nanoparticules d'oxyde de fer^[9],[10], sont devenus utilisables. Ces agents apparaissent très foncés sur les images pondérées en T^*
₂ et peuvent être utilisées pour l'imagerie hépatique, car le tissu hépatique normal retient l'agent, ce que ne font pas les zones anormales (par exemple, cicatrices, tumeurs). Ils peuvent également être pris par voie orale, pour améliorer la visualisation de l'appareil digestif et pour empêcher l'eau dans l'appareil digestif d'obscurcir d'autres organes (par exemple, le pancréas). Des agents diamagnétiques tels que le sulfate de baryum ont également été étudiés pour une utilisation potentielle dans l'appareil digestif, mais sont moins fréquemment utilisés.

Espace réciproque (k-space)

En 1983, Ljunggren ^[11] et Twieg ^[12] indépendamment introduit le formalisme de l'espace réciproque, une technique qui s'est avérée inestimable pour unifier différentes techniques d'imagerie RM. Ils ont montré que le signal MR démodulé S (t) généré par précession libre de spins nucléaires en présence d'un gradient de champ magnétique linéaire G est égal à la transformation de Fourier de la densité de spin effective. Mathématiquement :

${\displaystyle S(t)={\tilde {\rho }_{\mathrm {eff} }\left({\vec {k}(t)\right)\equiv \int _{-\infty }^{\infty }\mathrm {d} {\vec {x}\ \rho ({\vec {x})\cdot e^{2\pi i\ {\vec {k}(t)\cdot {\vec {x}$

où:

${\displaystyle {\vec {k}(t)\equiv \int _{0}^{t}{\vec {G}(\tau )\ \mathrm {d} \tau }$

En d'autres termes, à mesure que le temps progresse, le signal trace une trajectoire dans l'espace réciproque avec le vecteur vitesse de la trajectoire proportionnel au vecteur du gradient de champ magnétique appliqué. Par le terme densité de spin effective, nous entendons la vraie densité de spin ${\displaystyle \rho ({\vec {x})}$ corrigé des effets de la préparation de T₁, de la désintégration de T₂, du déphasage dû à l'inhomogénéité du champ, du flux, de la diffusion, etc. et de tout autre phénomène qui affecte la quantité de magnétisation transversale disponible pour induire un signal dans la sonde RF ou sa phase par rapport au champ électromagnétique de la bobine réceptrice.

À partir de la formule de base de l'espace réciproque, il s'ensuit immédiatement que nous reconstruisons une image ${\displaystyle I({\vec {x})}$ simplement en prenant l'inverse de la transformation de Fourier des données échantillonnées, à savoir :

${\displaystyle I\left({\vec {x}\right)=\int _{-\infty }^{\infty }\mathrm {d} {\vec {k}\ S\left({\vec {k}(t)\right)\cdot e^{-2\pi i\ {\vec {k}(t)\cdot {\vec {x}$

En utilisant le formalisme de l'espace réciproque, un certain nombre d'idées paraissant complexes sont devenues simples. Par exemple, il devient très facile de comprendre le rôle de l'encodage de phase (la méthode dite du spin-warp). Dans un écho de spin standard ou un balayage d'écho de gradient, où le gradient de lecture (ou de vue) est constant (par exemple, G), une seule ligne d'espace réciproque est balayée par excitation radiofréquence. Lorsque le gradient de codage de phase est nul, la ligne balayée est l'axe k_x. Lorsqu'une impulsion de codage de phase non nulle est ajoutée entre l'excitation RF et le début du gradient de lecture, cette ligne se déplace vers le haut ou vers le bas dans l'espace réciproque, c'est-à-dire que nous balayons la ligne k_y = constant.

Le formalisme de l'espace réciproque permet également de comparer très facilement différentes techniques de numérisation. En imagerie "echo-planar" (EPI) à un seul coup, tout l'espace réciproque est balayé en un seul coup, suivant une trajectoire sinusoïdale ou en zigzag. Étant donné que les lignes alternées de l'espace réciproque sont balayées dans des directions opposées, cela doit être pris en compte dans la reconstruction. Les techniques d'EPI^[Quoi ?] multi-coups et d'écho de spin rapide n'acquièrent qu'une partie de l'espace réciproque par excitation. Dans chaque plan, un segment entrelacé différent est acquis et les plans sont répétés jusqu'à ce que l'espace réciproque soit suffisamment bien couvert. Puisque les données au centre de l'espace réciproque représentent les fréquences spatiales plus faibles que les données sur les bords, la valeur T_E pour le centre de l'espace réciproque détermine le contraste T₂ de l'image.

L'importance du centre de l'espace réciproque dans la détermination du contraste de l'image peut être exploitée dans des techniques d'imagerie plus avancées. Une de ces techniques est l'acquisition en spirale — un gradient de champ magnétique rotatif est appliqué, provoquant une spirale de la trajectoire dans l'espace réciproque du centre vers le bord. En raison de T₂ et T^*
₂ décroissants, le signal est le plus élevé au début de l'acquisition, donc l'acquisition du centre de l'espace réciproque améliore d'abord le rapport contraste / bruit (CNR, pour Contrast to Noise Ratio en anglais) par rapport aux acquisitions en zigzag classiques, en particulier en présence de mouvement rapide.

Puisque ${\displaystyle {\vec {x}$ et ${\displaystyle {\vec {k}$ sont des variables conjuguées (par rapport à la transformation de Fourier) on peut utiliser le théorème de Nyquist pour montrer que le pas dans l'espace réciproque (k-space) détermine le champ de vision de l'image (fréquence maximale correctement échantillonnée) et la valeur maximale de k échantillonnée détermine La résolution ; c’est-à-dire,

${\displaystyle {\rm {FOV}\propto {\frac {1}{\Delta k}\qquad \mathrm {Resolution} \propto |k_{\max }|\ .}$

(Ces relations s'appliquent à chaque axe indépendamment. )

Exemple de séquence d'impulsions

Dans le chronogramme, l'axe horizontal représente le temps. L'axe vertical représente :

• Pour la rangée du haut : L'amplitude des impulsions de radiofréquence ;
• Pour les rangées médianes : Amplitudes des trois impulsions de gradient de champ magnétique orthogonales ;
• Pour la rangée du bas : Un convertisseur analogique-numérique (ADC) en réception.

Les radiofréquences sont transmises à la fréquence de Larmor du nucléide à imager. Par exemple, pour ¹H dans un champ magnétique de 1T, une fréquence de 42,5781   MHz serait utilisé. Les trois gradients de champ sont étiquetés G_X (correspondant généralement à la direction gauche-droite d'un patient et colorés en rouge dans le diagramme), G_Y (correspondant généralement à la direction avant-arrière d'un patient et colorés en vert dans le diagramme), et G_Z (correspondant généralement à la direction de la tête aux pieds d'un patient et colorée en bleu dans le diagramme). Lorsque des impulsions de gradient négatives sont représentées, elles représentent une inversion de la direction du gradient, c'est-à-dire de droite à gauche, d'arrière en avant ou de pointe à tête. Pour l'imagerie humaine, des intensités de gradient de 1 à 100 mT/m sont utilisés : des intensités de gradient plus élevées permettent une meilleure résolution et une imagerie plus rapide. La séquence d'impulsions montrée ici produirait une image transversale (axiale).

La première partie de la séquence d'impulsions, SS (pour Slice Selection en anglais), réalise une "sélection de tranche". Une impulsion façonnée (représentée ici avec une modulation sinc) provoque une nutation à 90° de la magnétisation nucléaire longitudinale à l'intérieur d'une dalle, ou tranche, créant une magnétisation transversale. La deuxième partie de la séquence d'impulsions, PE, confère un déphasage à la magnétisation nucléaire sélectionnée par tranche, variant avec son emplacement dans l'axe Y. La troisième partie de la séquence d'impulsions, une autre sélection de tranche (de la même tranche) utilise une autre impulsion façonnée pour provoquer une rotation de 180 ° de la magnétisation nucléaire transversale à l'intérieur de la tranche. Cette aimantation transversale se recentre pour former un écho de spin à un instant T_E. Pendant l'écho de spin, un encodage de fréquence (FE, pour Frequency-Encoding en anglais) ou gradient de lecture est appliqué, faisant varier la fréquence de résonance de la magnétisation nucléaire avec son emplacement dans l'axe X. Le signal est échantillonné n_FE fois par l'ADC pendant cette période, comme représenté par les lignes verticales. En général, n_FE est compris entre 128 et 512 échantillons prélevés.

L'aimantation longitudinale est alors autorisée à récupérer quelque peu et après un temps T_R la séquence entière est répétée n_PE fois, mais avec le gradient de codage de phase incrémenté (indiqué par les hachures horizontales dans le bloc de gradient vert). En règle générale, n_PE est compris entre 128 et 512 répétitions effectuées.

Les lobes négatifs dans G_X et G_Z sont imposés pour garantir qu'au temps T_E (le maximum d'écho de spin), la phase n'encode la localisation spatiale que dans la direction Y.

Typiquement, T_E est compris entre 5ms et 100ms, tandis que T_R est compris entre 100ms et 2000ms.

Après la matrice bidimensionnelle (dimension typique entre 128×128 et 512×512) a été acquise, produisant les données dites d'espace réciproque, une transformation de Fourier inverse bidimensionnelle est effectuée pour fournir l'image RM. Soit la magnitude, soit la phase de la transformation de Fourier peuvent être prises, la première étant beaucoup plus courante.

Aperçu des principales séquences

Ce tableau n'inclut pas les séquences inhabituelles et expérimentales.

Groupe	Séquence	Abr.	Physiques	Principales distinctions cliniques	Exemple
Spin echo	T1 weighted	T1	Mesure de la relaxation spin–réseau en utilisant un temps de répétition (TR) et un temps d'écho (TE) courts.	Signal faible pour indiquer une plus forte proportion d'eau[13], comme pour un dème, une tumeur, un infarctus, une inflammation, une infection, une hémorragie traumatique ou non traumatique[14]. Signal fort pour la présence de graisse[Quoi ?][13],[14] Signal fort pour les substances paramagnétiques, telles que les produits de contraste pour l'imagerie par résonance magnétique[14] Standard foundation and comparison for other sequences
	T2 weighted	T2	Mesure de la relaxation spin – spin en utilisant des temps TR et TE longs.	Signal fort pour la présence plus importante d'eau[13] Signal faible pour la présence de graisse[13] Signal faible pour les substances paramagnétiques[14] Standard foundation and comparison for other sequences
	Proton density weighted	PD	TR long pour réduire T1 et TE court pour minimiser T2[15].	Joint disease and injury[16]. High signal from meniscus tears[17]. (pictured)
Gradient echo (GRE)	Steady-state free precession	SSFP	Maintien d'une magnétisation transversale résiduelle constante sur des cycles successifs[18].	Creation of cardiac MRI videos (pictured)[18].
	Effective T2 or "T2-star"	T2*	Postexcitation refocused GRE with small flip angle[19].	Low signal from hemosiderin deposits (pictured) and hemorrhages[19].
Inversion recovery	Short tau inversion recovery	STIR	Fat suppression by setting an inversion time where the signal of fat is zero[20].	High signal in edema, such as in more severe stress fracture[21]. Shin splints pictured:
	Fluid-attenuated inversion recovery	FLAIR	Fluid suppression by setting an inversion time that nulls fluids	High signal in lacunar infarction, multiple sclerosis (MS) plaques, subarachnoid haemorrhage and meningitis (pictured)[22].
	Double inversion recovery	DIR	Simultaneous suppression of cerebrospinal fluid and white matter by two inversion times[23].	High signal of multiple sclerosis plaques (pictured)[23].
Diffusion weighted (DWI)	Conventional	DWI	Measure of Brownian motion of water molecules[24].	High signal within minutes of cerebral infarction (pictured)[25].
	Apparent diffusion coefficient	ADC	Reduced T2 weighting by taking multiple conventional DWI images with different DWI weighting, and the change corresponds to diffusion[26].	Low signal minutes after cerebral infarction (pictured)[27].
	Diffusion tensor	DTI	Mainly tractography (pictured) by an overall greater Brownian motion of water molecules in the directions of nerve fibers[28].	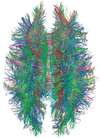Evaluating white matter deformation by tumors[28] Reduced fractional anisotropy may indicate dementia[29].
Perfusion weighted (PWI)	Dynamic susceptibility contrast	DSC	Gadolinium contrast is injected, and rapid repeated imaging (generally gradient-echo echo-planar T2 weighted) quantifies susceptibility-induced signal loss[30].	In cerebral infarction, the infarcted core and the penumbra have decreased perfusion (pictured)[31].
	Dynamic contrast enhanced	DCE	Measuring shortening of the spin–lattice relaxation (T1) induced by a gadolinium contrast bolus[32].
	Arterial spin labelling	ASL	Magnetic labeling of arterial blood below the imaging slab, which subsequently enters the region of interest[33]. It does not need gadolinium contrast[34].
Functional MRI (fMRI)	Blood-oxygen-level dependent imaging	BOLD	Changes in oxygen saturation-dependent magnetism of hemoglobin reflects tissue activity[35].	Localizing highly active brain areas before surgery, also used in research of cognition[36].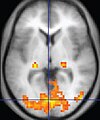
Magnetic resonance angiography (MRA) and venography	Time-of-flight	TOF	Blood entering the imaged area is not yet magnetically saturated, giving it a much higher signal when using short echo time and flow compensation.	Detection of aneurysm, stenosis, or dissection[37]
	Phase-contrast magnetic resonance imaging	PC-MRA	Two gradients with equal magnitude, but opposite direction, are used to encode a phase shift, which is proportional to the velocity of spins[38].	Detection of aneurysm, stenosis, or dissection (pictured)[37].	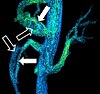(VIPR)
Susceptibility-weighted		SWI	Sensitive for blood and calcium, by a fully flow compensated, long echo, gradient recalled echo (GRE) pulse sequence to exploit magnetic susceptibility differences between tissues	Detecting small amounts of hemorrhage (diffuse axonal injury pictured) or calcium[39].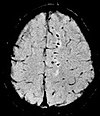

Scanner IRM

Construction et exploitation

Les principaux composants d'un scanner IRM sont : l'aimant principal, qui polarise l'échantillon, les bobines de calage pour corriger les inhomogénéités dans le champ magnétique principal, le système de gradient qui est utilisé pour localiser le signal RM et le système RF, qui excite l'échantillon et détecte le signal RMN résultant. L'ensemble du système est contrôlé par un ou plusieurs ordinateurs.

L'aimant

Fichier audio

Audio recording

A short extract of a 20-minute scanning session, recorded outside the above unit

modifier

L'aimant est le composant le plus gros et le plus cher du scanner, et le reste du scanner est construit autour de lui. La force de l'aimant est mesurée en teslas (T) . Les aimants cliniques ont généralement une intensité de champ comprise entre 0,1 et 3,0T, avec des systèmes de recherche disponibles jusqu'à 9,4T à usage humain et 21T pour les systèmes animaux^[40]. Aux États-Unis, des intensités de champ jusqu'à 4T ont été approuvés par la FDA pour une utilisation clinique^[41].

La précision est tout aussi importante que la force de l'aimant principal. La rectitude des lignes magnétiques au centre (ou, comme on le sait techniquement, l'isocentre) de l'aimant doit être presque parfaite. C'est ce qu'on appelle l'homogénéité. Les fluctuations (inhomogénéités de l'intensité du champ) dans la zone de balayage doivent être inférieures à trois parts par million (3 ppm). Trois types d'aimants ont été utilisés :

• L'aimant permanent : des aimants conventionnels fabriqués à partir de matériaux ferromagnétiques (par exemple, des alliages d'acier contenant des éléments de terres rares tels que le néodyme) peuvent être utilisés pour fournir le champ magnétique statique. Un aimant permanent suffisamment puissant pour être utilisé dans une IRM sera extrêmement grand et encombrant ; ils peuvent peser plus de 100 tonnes. Les IRM à aimant permanent sont très peu coûteuses à entretenir ; cela ne peut pas être dit des autres types d'aimants IRM, mais l'utilisation d'aimants permanents présente des inconvénients importants. Ils ne sont capables d'atteindre que de faibles intensités de champ par rapport aux autres aimants IRM (généralement inférieurs à 0,4T) et ils sont d'une précision et d'une stabilité limitées. Les aimants permanents présentent également des problèmes de sécurité particuliers ; comme leurs champs magnétiques ne peuvent pas être « désactivés », les objets ferromagnétiques sont pratiquement impossibles à en retirer une fois qu'ils sont en contact direct. Les aimants permanents nécessitent également une attention particulière lorsqu'ils sont amenés sur leur site d'installation.
• L'électroaimant résistif : Un solénoïde enroulé en fil de cuivre est une alternative à un aimant permanent. Un avantage est le faible coût initial, mais l'intensité et la stabilité du champ sont limitées. L'électroaimant nécessite une énergie électrique considérable pendant son fonctionnement, ce qui peut rendre son fonctionnement coûteux. Cette conception est essentiellement obsolète.
• L'électroaimant supraconducteur : Lorsqu'un alliage niobium-titane ou niobium-étain est refroidi par l'hélium liquide à 4K (−269 °C, −268,9 °C) il devient un supraconducteur, perdant sa résistance au flux de courant électrique. Un électroaimant construit avec des supraconducteurs peut avoir des intensités de champ et une stabilité extrêmement élevés. La construction de tels aimants est extrêmement coûteuse et l'hélium cryogénique est coûteux et difficile à manipuler. Cependant, malgré leur coût, les aimants supraconducteurs refroidis à l'hélium sont le type le plus courant que l'on trouve aujourd'hui dans les scanners IRM.

La plupart des aimants supraconducteurs ont leurs bobines de fil supraconducteur immergées dans de l'hélium liquide, à l'intérieur d'un récipient appelé cryostat. Malgré une isolation thermique, comprenant parfois un deuxième cryostat contenant de l'azote liquide, la chaleur ambiante fait bouillir lentement l'hélium. De tels aimants nécessitent donc un complément régulier en hélium liquide. En général, un dispositif de refroidissement cryogénique, également connu sous le nom de coldhead, est utilisé pour re-condenser une partie du retour de la vapeur d'hélium dans le bain d'hélium liquide. Plusieurs fabricants proposent désormais des scanners « sans cryogène », où au lieu d'être immergé dans l'hélium liquide, le fil magnétique est refroidi directement par un cryocooler^[42]. Une autre technique pour refroidir l'aiment consiste à placer soigneusement l'hélium liquide dans des endroits stratégiques, réduisant considérablement la quantité d'hélium liquide à utiliser^[43], ou, des supraconducteurs à haute température peuvent être utilisés à la place^[44],[45].

Les aimants sont disponibles dans une variété de formes. Cependant, les aimants permanents sont le plus souvent en forme de « C » et les aimants supraconducteurs sont le plus souvent de forme cylindrique. Des aimants supraconducteurs en forme de C et des aimants permanents en forme de boîte ont également été utilisés.

L'intensité du champ magnétique est un facteur important pour déterminer la qualité de l'image. Des champs magnétiques plus élevés augmentent le rapport signal / bruit, permettant une résolution plus élevée ou un balayage plus rapide. Cependant, des intensités de champ plus élevées nécessitent des aimants plus coûteux avec des coûts de maintenance plus élevés et présentent des problèmes de sécurité accrus. Une intensité de champ de 1,0T à 1,5T est un bon compromis entre coût et performances pour un usage médical général. Cependant, pour certaines utilisations spécialisées (par exemple, l'imagerie cérébrale), des intensités de champ plus élevées sont souhaitables, certains hôpitaux utilisant désormais des scanners pouvant avoir des champs de 3,0T.

Les cales, ou "shims" en anglais

Lorsque le scanner RM est placé dans un hôpital ou dans une clinique, son champ magnétique principal est loin d'être suffisamment homogène pour être utilisé pour la numérisation. C'est pourquoi avant de procéder à un réglage fin du champ à l'aide d'un échantillon, le champ magnétique de l'aimant doit être mesuré et calé.

Une fois qu'un échantillon est placé dans le scanner, le champ magnétique principal est déformé par les limites de susceptibilité dans cet échantillon, provoquant une perte de signal (régions ne montrant aucun signal) et des distorsions spatiales dans les images acquises. Pour les humains ou les animaux, l'effet est particulièrement prononcé aux frontières air-tissu comme les sinus (en raison de l'oxygène paramagnétique dans l'air), ce qui rend par exemple les lobes frontaux du cerveau difficiles à imager. Pour restaurer l'homogénéité du champ, un jeu de bobines de calage est inclus dans le scanner. Ce sont des bobines résistives, généralement à température ambiante, capables de produire des corrections de champ réparties en plusieurs ordres d'harmoniques sphériques^[46].

Après avoir placé l'échantillon dans le scanner, le champ B₀ est « calé » en ajustant les courants dans les bobines de calage. L'homogénéité du champ est mesurée en examinant un signal FID en l'absence de gradients de champ. Le FID d'un échantillon mal calé montrera une enveloppe de désintégration complexe, souvent avec de nombreuses bosses. Les courants de calage sont ensuite ajustés pour produire un FID à décroissance exponentielle de grande amplitude, ce qui indique que le champ B₀ est homogène. Le processus est généralement automatisé^[47].

Les gradients

Des bobines de gradient sont utilisées pour encoder spatialement les positions des protons en faisant varier le champ magnétique linéairement à travers le volume d'imagerie. La fréquence de Larmor variera alors en fonction de la position dans les axes x, y et z.

Les bobines de gradient sont généralement des électroaimants résistifs alimentés par des amplificateurs sophistiqués qui permettent des ajustements rapides et précis de l'intensité et de la direction du champ. Les systèmes de gradient typiques sont capables de produire des gradients de 20 à 100 mT / m (c’est-à-dire que pour un aimant de 1,5 T, lorsqu'un gradient maximal de l'axe z est appliqué, l'intensité du champ peut être de 1,45 T à une extrémité d'un alésage de 1 m de long et 1,55 T à l'autre ^[48]). Ce sont les gradients magnétiques qui déterminent le plan d'imagerie - parce que les gradients orthogonaux peuvent être combinés librement, n'importe quel plan peut être sélectionné pour l'imagerie.

La vitesse de balayage dépend des performances du système de gradient. Des gradients plus forts permettent une imagerie plus rapide ou une résolution plus élevée ; de même, les systèmes à gradient capables d'une commutation plus rapide peuvent également permettre un balayage plus rapide. Cependant, les performances du gradient sont limitées par des problèmes de sécurité concernant la stimulation nerveuse.

Certaines caractéristiques importantes des amplificateurs de gradient et des bobines de gradient sont la vitesse de balayage et la force du gradient. Comme mentionné précédemment, une bobine de gradient créera un champ magnétique supplémentaire, variant linéairement, qui s'ajoute ou se soustrait au champ magnétique principal. Ce champ magnétique supplémentaire aura des composants dans les 3 directions, à savoir. x, y et z ; cependant, seule la composante le long du champ magnétique (généralement appelée axe z, donc notée G_z ) est utile pour l'imagerie. Le long de n'importe quel axe donné, le gradient s'additionnera au champ magnétique d'un côté de la position zéro et en soustraira de l'autre côté. Puisque le champ supplémentaire est un gradient, il a des unités de gauss par centimètre ou millitesla par mètre (mT / m). Les bobines de gradient haute performance utilisées en IRM sont généralement capables de produire un champ magnétique de gradient d'environ 30 mT / m ou plus pour un IRM de 1,5 T.

La vitesse de balayage d'un système de gradient est une mesure de la rapidité avec laquelle les gradients peuvent être activés ou désactivés. Les gradients de performance plus élevés typiques ont une vitesse de balayage allant jusqu'à 100–200 T·m⁻¹·s ⁻¹. La vitesse de balayage dépend à la fois de la bobine de gradient (il faut plus de temps pour faire monter ou descendre la puissance une grande bobine qu'une petite bobine) et des performances de l'amplificateur de gradient (il faut beaucoup de tension pour surmonter l'inductance de la bobine) et a une influence significative sur la qualité de l'image.

Système de radiofréquence

Le système de transmission radiofréquence (RF) se compose d'un synthétiseur RF, d'un amplificateur de puissance et d'une bobine de transmission . Cette bobine est généralement intégrée au corps du scanner. La puissance de l'émetteur est variable, mais les scanners corporels haut de gamme peuvent avoir une puissance de sortie maximale allant jusqu'à 35 kW^[49], et être capable de supporter une puissance moyenne de 1 kW. Bien que ces champs électromagnétiques soient dans la plage RF de dizaines de mégahertz (souvent dans la partie radio à ondes courtes du spectre électromagnétique) à des puissances dépassant généralement les puissances les plus élevées utilisées par la radio amateur, il y a très peu d'interférences RF produites par les appareils IRM. La raison en est que l'IRM n'est pas un émetteur radio. Le champ électromagnétique de fréquence RF produit dans la "bobine émettrice" est un champ magnétique proche avec très peu de composante de champ électrique changeante associée (comme toutes les transmissions d'ondes radio conventionnelles). Ainsi, le champ électromagnétique de haute puissance produit dans la bobine d'émetteur d'IRM ne produit pas beaucoup de rayonnement électromagnétique à sa fréquence RF, et la puissance est confinée à l'espace de la bobine et n'est pas rayonnée sous forme d'ondes radio. Ainsi, la bobine d'émission est un bon émetteur de champ électromagnétique à radiofréquence, mais un mauvais émetteur de rayonnement électromagnétique à radiofréquence.

Le récepteur se compose de la bobine, du préamplificateur et du système de traitement du signal. Le rayonnement électromagnétique RF produit par la relaxation nucléaire à l'intérieur du sujet est un véritable rayonnement EM (dans les ondes radio), et ceux-ci laissent le sujet sous forme de rayonnement RF, mais ils sont d'une puissance si faible qu'ils ne provoquent pas non plus d'interférences RF pouvant être captées par postes de radio à proximité (en outre, les scanners IRM sont généralement situés dans des pièces recouvertes de treillis métallique qui agissent comme des cages de Faraday. )

Bien qu'il soit possible de scanner en utilisant la bobine intégrée pour la transmission RF et la réception du signal MR, si une petite région est imagée, une meilleure qualité d'image (c'est-à-dire un rapport signal / bruit plus élevé) est obtenue en utilisant un plus petit bobine. Une variété de bobines qui s'adaptent étroitement autour de parties du corps telles que la tête, le genou, le poignet, la poitrine ou à l'intérieur, par exemple, le rectum sont disponibles.

Un développement récent de la technologie IRM a été le développement de bobines sophistiquées "multi-element phased array" ^[50] qui sont capables d'acquérir plusieurs canaux de données en parallèle. Cette technique « d'imagerie parallèle » utilise des schémas d'acquisition uniques qui permettent une imagerie accélérée, en remplaçant une partie de l'encodage spatial provenant des gradients magnétiques par la sensibilité spatiale des différents éléments de la bobine. Cependant, l'accélération accrue réduit également le rapport signal sur bruit et peut créer des artefacts résiduels dans la reconstruction d'image. Deux schémas d'acquisition et de reconstruction parallèles fréquemment utilisés sont connus sous le nom de SENSE ^[51] et GRAPPA^[52]. Un examen détaillé des techniques d'imagerie parallèle peut être trouvé ici^[53] :

Références

Bibliographie

• Portail de l’imagerie numérique