Projection Waterman papillon


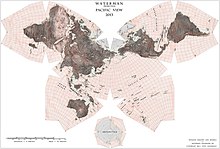


La carte du monde Waterman « Papillon » est une projection cartographique créée par Steve Waterman (en). Waterman publie pour la première fois une carte dans cet arrangement en 1996. L'arrangement est le déploiement d'un globe polyédrique en forme d'octaèdre tronqué, évoquant le principe de la carte papillon développé pour la première fois par Bernard JS Cahill (1866-1944) en 1909. Les cartes de Cahill et Waterman peuvent être présentées dans divers profils, généralement liés aux océans de l'Atlantique nord ou du Pacifique nord.
Cahill étant architecte, son approche tendait vers des formes qui pouvaient être démontrées physiquement, comme par exemple sa carte aplatie en forme de balle en caoutchouc. Waterman, quant à lui, dérive sa conception de ses travaux sur le compactage des sphères. Cela implique de connecter les centres des sphères cubiques compactées les plus proches dans une coque convexe correspondante, comme le montrent les graphiques ci-joints. Celles-ci illustrent l'amas de sphères W5, la coque convexe W5 et deux projections Waterman de la coque convexe W5.
Waterman a choisi le polyèdre W5 Waterman et le méridien central de 20°W pour minimiser l'interruption des principales masses terrestres. Popko note que la projection peut aussi être gnomonique[1]. Les deux méthodes donnent des résultats très similaires.
Pour projeter la sphère sur le polyèdre, la Terre est divisée en huit parties appenlées octants. Dans chaque octant, chaque méridien est dessiné sous forme de trois segments de ligne droite, chaque segment étant défini par ses extrémités sur deux des quatre « délinéations de lignes égales » définies par Waterman. Ces délimitations de lignes égales sont le pôle Nord, le bord du polyèdre le plus au nord, la plus longue ligne parallèle à l'équateur, et l'équateur lui-même. Les intersections de tous les méridiens avec une délimitation de ligne égale sont également espacées, et les intersections de tous les parallèles avec un méridien sont également espacées[2].
Tout comme la projection Dymaxion que Buckminster Fuller crée en 1943, une carte papillon octaédrique peut montrer tous les continents de manière ininterrompue si ses octants sont divisés au niveau d'un méridien approprié, tel que le méridien mi-atlantique 20°Ouest, et sont joints, par exemple, au niveau de l'Atlantique Nord, comme dans la version 1996[3],[4].
Voir aussi
- Liste des projections cartographiques
- Polyèdre de Waterman
- Bernard JS Cahill
- Carte du monde
- ↑ Popko Edward S., Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere, Taylor & Francis, , 20–21 p. (ISBN 9781466504295)
- ↑ Steve Waterman, "Waterman Projection Method", Waterman Project Website
- ↑ Gyorgy Darvias, Symmetry: Culture and Science, Symmetrion, , 129–171 p. (ISBN 963-214-761-8)
- ↑ Studio Dongo, The City That Traveled The World, CreateSpace Independent Publishing Platform, , cover and acknowledgements page (ISBN 9781484966228)