Rotor (météorologie)

Un rotor est un mouvement tourbillonnaire de l'air associé à des ondes orographiques. Il est localisé sous la partie laminaire et peut donner lieu à des turbulences extrêmement violentes qui peuvent briser un aéronef. Il est souvent matérialisé par des cumulus fractus (ou fractocumulus).
Cause

Un rotor est un phénomène météorologique associé à des ondes de gravité. L'air va osciller verticalement en aval de l'obstacle et en application directe des lois de conservation, des fluctuations du vent horizontal vont se produire. Des rouleaux vont donc se former et sont généralement le siège de turbulences qui sont amplifiées en fin de journée lorsque le sol est surchauffé.
Les ondes orographiques produisent des ascendances (et descendances) très puissantes où la vitesse verticale peut dépasser 10 m/s. Toutefois, près du sol l'air est instable car l'air en redescendant le long de la montagne se réchauffe suivant le gradient adiabatique sec (g/Cp). De plus, par temps clair, la sous-couche va être réchauffée à partir du sol et donc des ascendances thermiques vont se former. La combinaison de ces ascendances thermiques et des mouvements tourbillonnaires associé aux ondes orographiques va rendre l'air turbulent. Des sous-tourbillons vont se former.
La transition entre une rafale ascendante et une rafale descendante à l'intérieur du rotor peut s'effectuer sur une cinquantaine de mètres environ[1]. Des sous-tourbillons sont également formés à la limite amont entre le rotor principal et l'onde orographique proprement dite[2],[3]. Ceci est dû à un effet de cisaillement entre le tourbillon (rotor) et l'onde qui génère une instabilité de Kelvin-Helmholtz[3].
Types de rotor

Rolf Hertenstein a défini deux classes de rotors:
- les rotors associés à des ondes piégées (type I)
- et les rotors associés à un ressaut hydraulique[2] (type II).
Rotor associé à des ondes piégées
Ce type de rotor est de loin le plus courant. Les ondes sont quasi stationnaires et le mouvement de l'air dans le rotor lui-même est quasi circulaire. En général la turbulence à l'intérieur du rotor est de faible à sévère mais en pratique jamais extrême. Ces rotors sont souvent matérialisés par une ligne de nuages en rouleau constituée de cumulus ou cumulus fractus. Ces nuages, peu épais, se situent en général au niveau de la ligne de crête.
Une explication simple et élégante de la formation de rotors associés à des ondes piégées a été donnée par Paul Queney[4],[1] et Richard Scorer[5].
Cette théorie est basée sur une version simplifiée de l'équation de Scorer. Cette théorie est appelée modèle de l'œil de chat car les lignes de courant en aval d'une chaîne de montagnes ont la forme d'un œil de félin (figure 5 dans la boîte déroulante, elles sont aussi montrées de manière approximative dans la figure 8). Cette théorie est basée sur la loi de conservation de la masse. En particulier, cette théorie explique pourquoi le vent au sol sous un rotor est souvent inversé et que le rotor a la forme d'un tambour horizontal. Ce modèle est un modèle bi-dimensionnel en (x,z) et donc s'appuie sur des hypothèses simplificatrices.
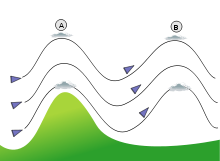
On considère un modèle en 2 dimensions où la chaîne de montagnes est rectiligne et de hauteur constante. On suppose qu'à l'amont de la montagne, le champ de vitesses est axisymétrique et est de la forme :
où pour et que sinon.
On suppose qu'à l'aval de la montagne se forment des ondes stationnaires que l'on modèle par un champ de vitesses de type et l'on cherche à exprimer .
On écrit :
Comme la vitesse du vent est très nettement inférieure à la vitesse du son, on peut considérer le fluide comme étant incompressible et donc l'on a :
et donc il existe une fonction de courant telle que :
On suppose que le flot est barotropique et que la perturbation du flot est irrotationnelle. On a donc :
On vérifie alors aisément que
On suppose que l'extension horizontale du phénomène par rapport à l'extension verticale est très grande et donc que :
On obtient alors :
La solution générale de cette équation laplacienne est donc :
On définit la fonction de courant globale comme étant :
On vérifie aisément que :
Il est clair qu'à z = 0, on a w(x,0) = 0. On obtient donc et on peut donc supposer que
On obtient donc :
On suppose que la fonction est périodique et que g(x) peut être représentée par une fonction sinusoïdale. On écrit alors :
Soit N la fréquence de Brunt-Väisälä. On suppose que le nombre d'onde k vaut :
La vitesse du vent vertical est donnée par :
Et donc :
k est le nombre d'onde défini par :
où N est la fréquence de Brunt-Väisälä.
On déterminera a infra.
On rappelle que et donc :
Le vent horizontal en aval sera donc :
On constate alors que près du sol, le vent sera inversé lorsque c'est-à-dire:
On remarque que
La trajectoire d'une parcelle d'air suivra donc les lignes de niveau définies par .
On va démontrer que la circulation d'air se décompose en une boucle fermée appelée rotor et un courant synoptique.
Une ligne de courant est donc définie par :
On pose On rappelle que
On substitue et donc :
Une telle courbe en (z,t) est une courbe elliptique et donc est une courbe de genre 1. Une telle courbe est donc constituée d'une boucle et d'une courbe partant à l'infini.
Dans le cas C = 0 la courbe est polynomiale (et se factorise) et l'on a :
Les solutions explicites en ce qui concerne les lignes de courant sont les suivantes :
Dans le cas C = 0, on a :
Le sommet du rotor est donc situé à . Si l'on fait l'hypothèse supplémentaire que le rotor se situe au niveau de la ligne de crête, connaissant γ (donné par les conditions synoptiques), on peut en déduire a. Soit h la hauteur de la montagne, on a alors :
et donc :
On obtient donc la vitesse verticale suivante :
Donc, si l'on prend h = 2000 m, γ = 0.02 s¯¹, N= 0.01 Hz, UM = 40 m/s, à 1000 mètres d'altitude, le courant ascendant maximum sera :
- m/s
À 2000 mètres, l'ascendance sera de 5 m/s. Ces valeurs numériques correspondent grossièrement aux courants ascendants habituellement relevés.
La figure ci-dessous représente les lignes de courant pour k = 0.001 m¯¹, a = 20 m/s, γ = 0.02 s¯¹.

La turbulence est maximale en amont et au-dessus du rotor. De plus, les vitesses ascensionnelles les plus élevées se trouvent juste en amont du rotor comme les courbes de température isentropique le montrent dans la référence (Grubišić, 2004)[6]. De plus, lorsque le rotor est matérialisé par un nuage-mur, l'ascendance devient encore plus forte à cause de la libération de chaleur latente. Dans les cas extrêmes, on peut avoir affaire à un rotor de type II qui est décrit ci-dessous.
Rotor de ressaut hydraulique


Ce type de rotor est rare et est semble-t-il associé à une inversion marquée de température au sommet de la montagne. Les simulations numériques effectuées semblent confirmer le phénomène[7]. En outre ces rotors ont tendance à se produire en fin d'après midi lorsque le sol est surchauffé[8]. Ces rotors sont extrêmement violents et peuvent atteindre des altitudes élevées (jusqu'à 7 km au-dessus du sol). Ces rotors peuvent être matérialisés par des nuages dont le flanc au vent est quasi vertical et dont la hauteur peut atteindre 8 000 à 9 000 mètres[1]. Ceci peut s'expliquer par le fait que l'air est en forte ascension dans le nuage et donc empêche les gouttelettes d'eau ou cristaux de glace de redescendre vers le sol. À titre d'illustration, l'image ci-contre montre un ressaut hydraulique où la turbulence est semble-t-il intense. La figure 5 de la référence Hertenstein, 2005[2] montre un nimbostratus de grande extension verticale associé à un ressaut hydraulique.
Au cours du Sierra Wave Project, un pilote de planeur (Larry Edgar) avait rencontré le une turbulence extrême en entrant dans un nuage de rotor qui grandit considérablement en l'espace de quelques secondes. Le planeur s'était engouffré dans le nuage et le planeur eut subi des accélérations gigantesques (16 g)[1],[9],[10],[11] qui brisèrent l'aéronef, blessèrent le pilote qui fut aussi victime d'un voile noir. Il semblerait que le pilote de planeur eût rencontré un rotor de type II (ressaut hydraulique). Le pilote bien que blessé put s'éjecter en parachute[12].
Les figures 6 et 7 montrent un phénomène de ressaut hydraulique en aval de chutes naturelle et artificielle. En particulier, la figure 7 montre un double ressaut hydraulique.
Rotors migratoires
Ces rotors sont des tourbillons se déplaçant dans le sens du vent à une vitesse inférieure à celle du vent synoptique. Ils se forment en général en présence d'une activité thermique ou après le passage d'un front froid[13]. Ils sont souvent matérialisés par des petits cumulus fractus et peuvent souvent être confondus avec des ascendances thermiques. Les fractocumulus marquant ces rotors ont un mouvement en apparence circulaire[13]. Ces rotors ont une durée de vie relativement courte qui est de l'ordre de quelques minutes[13].
Rotors associés à des cyclones tropicaux
Sous l'ouragan Fran, Joshua Wurman a identifié un mouvement tourbillonnaire d'axe horizontal s'apparentant à des rotors associés à des ondes orographiques. La distance entre 2 rouleaux était de l'ordre de 600 m. La vitesse du vent synoptique à 1 000 mètres était de 50 à 60 m/s (100 à 120 nœuds) alors qu'en certains endroits au sol, le vent n'était que de 15 à 35 m/s (30 à 70 nœuds). Ces rotors étaient parallèles à la direction générale du vent. La partie descendante du rotor engendrait des vents au sol de 120 nœuds tandis que la partie ascendante du rotor ralentissait les vents au sol de l'ordre de 30 à 70 nœuds[14].
Vol à voile
Turbulence

Soit d la distance entre une rafale montante et descendante, soit ±w la vitesse de la rafale verticale et soit v la vitesse horizontale de l'aéronef. L'accélération que l'aéronef va subir sera :
Donc, plus l'aéronef volera vite, plus les accélérations seront importantes.
La différence de vitesse verticale entre les deux rafales peut être de l'ordre de 20 m/s. Un aéronef (avion de ligne) qui traverserait cette zone à 300 nœuds (150 m/s) va donc subir une accélération verticale de 6 g (60 m/s2) et va donc probablement se briser. Toutefois, les planeurs sont beaucoup plus lents. En supposant que le planeur traverse le rotor à 40 nœuds (20 m/s), l'accélération verticale sera seulement de 0,8 g ce qui est nettement en deçà des limites de vol.
La turbulence peut être définie de manière plus rigoureuse en introduisant la notion de tourbillon (parfois appelée « vorticité » par calque de l'anglais) qui est définie de la manière suivante[15] :
où v est le champ de vecteurs vitesse. Le tourbillon est exprimé en s¯¹. Ainsi, le facteur de charge subi par un aéronef sera :[Note 2]
Au cours de l'expérience T-REX, des tourbillons de 0,4 s¯¹ ont été estimés[16]. Ainsi, un avion de ligne volant à 200 m/s subira un facteur de charge de 10 + 0.4 × 200/2 = 50 m/s2. Ce qui correspondrait à 5 fois l'accélération de la gravité ce qui est suffisant pour détruire l'aéronef. Lors de l'accident du Boeing 737 à Colorado Springs, il a été estimé que le tourbillon a pu atteindre 0.6 s¯¹[17].
A contrario, un tourbillon de 0,4 Hz appliqué à un planeur volant à 20 m/s engendre un facteur de charge de seulement 8 m/s2, ce qui est moins que l'accélération de la pesanteur et donc ne détruira en aucun cas ce type d'aéronef.
On peut aussi remarquer que le tourbillon est maximal à l'avant du rotor et donc la turbulence sera maximale dans la zone de transition entre le rotor et la partie laminaire de l'onde traduisant une instabilité de Kelvin-Helmholtz à la jonction des deux masses d'air[16],[18].
La turbulence est « acceptable » du côté au vent (de faible à modérée) (partie ascendante du rotor), tandis qu'elle peut être sévère à extrême du côté sous le vent (partie descendante du rotor)[19]. Ainsi, un planeur peut exploiter la partie ascendante du rotor sans prendre trop de risques alors que la partie descendante accumule 2 problèmes : le planeur se retrouve rapidement au sol et les turbulences peuvent être dangereuses.
Exploitation du rotor

De plus, les rotors sont relativement bien organisés et il est donc possible pour un bon pilote de planeur d'exploiter les ascendances thermiques et les ascendances liées au rotor lui-même. Ainsi, on notera que la dimension d'un rotor est de l'ordre de 1 à 2 kilomètres. Toutefois, ce rotor, qui est relativement étendu, est composé de sous-tourbillons dont l'étendue est de l'ordre de quelques dizaines de mètres. Les rotors de type I sont peu dangereux pour le vélivole si celui-ci se déplace suffisamment lentement et reste à l'extérieur du nuage. Au cours de l'ascension à l'intérieur d'un rotor, le pilote devra ouvrir le virage du côté au vent et resserrer le virage du côté sous le vent.
Lorsque le planeur a atteint une altitude suffisante à l'intérieur du rotor, le pilote va se diriger en direction de la montagne pour contacter l'onde proprement dite. Juste avant de contacter l'onde elle-même, le planeur va être soumis aux très forts sous-tourbillons mentionnés plus haut. Le pilote va subir pendant un temps très court (de l'ordre de quelques secondes) une très forte turbulence [19] puis le pilote aura l'impression de voler dans de l'huile avec le variomètre souvent bloqué en montée[20].
Comme le rotor correspond à une séparation du flot en altitude avec le sol (théorie de l'œil de chat de Paul Queney), le long de la ligne de séparation entre les deux systèmes (onde laminaire et rotor), la température potentielle sera uniforme le long de cette ligne de séparation. Ainsi si l'air est suffisamment humide, un nuage (cumulus fractus) va se former dans la partie supérieure du rotor. Comme il y a libération de chaleur latente dans le rotor, l'air va devenir instable et donc des turbulences extrêmes vont se former à l'intérieur de ce cumulus à l'air faussement inoffensif[21]. Ceci explique pourquoi plusieurs pilotes ont brisé leur machines en volant dans ces soi-disant nuages inoffensifs[1],[9],[11].
L'exploitation d'un rotor migratoire s'apparente à un travail de Sisyphe. En effet ces rotors dérivent lentement dans le sens du vent et disparaissent au bout de quelques minutes. Le pilote aura donc été poussé vers l'arrière et devra remonter face au vent pour contacter un nouveau rotor. Cette stratégie ne sera valable que si la perte d'altitude en remontant face au vent est inférieure au gain d'altitude à l'intérieur du rotor. Comme la vitesse du vent est supérieure à la vitesse de déplacement du rotor, à chaque cycle, le pilote spiralant dans le rotor devra ouvrir le virage face au vent[13].
Mesures à l'intérieur des rotors
50 ans après le Sierra Wave Project un projet similaire de mesures à l'intérieur d'un système ondulatoire a été effectué en mars- ayant pour nom « Sierra Rotors Project ». Les résultats des mesures ont été comparés avec des simulations numériques et ces mesures ont montré qu'au premier ressaut, les rotors pouvaient atteindre 6 000 m soit 20 000 pieds et peuvent affecter des aéronefs volant nettement au-dessus de la ligne de crêtes[22],[23].
Effets terrestres et maritimes
Comme dans le cas de l'effet de foehn, les rotors peuvent se rendre au sol lorsque les conditions sont propices. Ils peuvent alors donner des rafales importantes en aval des montages qui causent des dégâts aux infrastructures, comme les bâtiments, ou donnent des vents de travers qui vont renverser des véhicules sur les routes ou des aéronefs dans les aéroports.
Lorsqu'ils se propagent sur un plan d'eau ils peuvent également affecter la navigation. Par exemple, les voiliers de type Gréement bermudien sont vulnérables aux rotors. En aval d'îles de taille modeste mais d'altitude élevée, des ondes orographiques se forment comme au-dessus la Mer Adriatique en Dalmatie ou au-dessus la Mer Égée. Ces ondes engendrent des rotors dans la couche sous-laminaire et donc de la turbulence horizontale et verticale. La maîtrise du voilier devient alors problématique car la poussée du vent ordinaire dans la voile disparaît lorsque la voile devient horizontale. Le voilier peut alors chavirer. Les marins nomment cette condition rafale descendante ce qui est incorrect car ces rafales ne sont pas associées à des orages, ce sont en fait des tourbillons horizontaux.
Notes et références
Notes
- ↑ Les remous de la figure 7 ressemblent fortement à des cumulus de rotor dans lesquels il serait fort imprudent de s'aventurer.
- ↑ La formule est démontrée dans l'article Dynamique du vol en présence de rafales.
Références
- (en) Joachim Kuettner, Rolf Hertenstein, « Observations of mounain-induced rotors and related hypotheses: a review », Proceedings of the 10th AMS Conference on Mountain Meteorology, American meteorological society, , p. 2 (lire en ligne [PDF])
- Types of Rotor
- (en) James Doyle, Dale Durran, « Rotor and Subrotor Dynamics in the Lee of Three-Dimensional Terrain », Journal of the atmospheric sciences, American meteorological society, no 64, , p. 4218-4219 (lire en ligne [PDF])
- ↑ (en)Paul Queney, « Rotor Phenomena in the Lee of Mountains », Tellus, vol. VII, no 3, (DOI 10.3402/tellusa.v7i3.8873, lire en ligne)
- ↑ Theory of mountain waves, p. 131-143
- ↑ (en)Vanda Grubišić, Stephen Cohn, Sierra rotors project: preliminary findings, , PDF (lire en ligne)
- ↑ (en) Rolf Hertenstein, « The Influence of Inversions on Rotors », Monthly weather review, American meteorological society, (lire en ligne)
- ↑ (en) James Doyle, Dale Durran, « The Dynamics of Mountain-Wave-Induced Rotors », Journal of the atmospheric sciences, American meteorological society, vol. 59, , p. 199 (lire en ligne [PDF], consulté le )
- Article de Kuettner, p. 6
- ↑ (en) Robert F Whelan, Exploring the monster : Mountain lee waves : the aerial elevator, Wind Canyon Books, , 169 p. (ISBN 978-1-891118-32-6), p. 141
- (en) Bob Spielman, « Glider crash », Soaring, Soaring Society of America, , p. 32-36
- ↑ Riding on Air, p. 61
- Danse avec le vent, p. 174
- ↑ (en) Joshua Wurman, « Intense Sub-Kilometer-Scale Boundary Layer Rolls Observed in Hurricane Fran », Science, vol. 280, , p. 555 (DOI 10.1126/science.280.5363.555, lire en ligne [PDF])
- ↑ Organisation météorologique mondiale, « Tourbillon », sur Eumetcal (consulté le )
- Expérience T-REX, p. 1247
- ↑ (en) Uncontrolled Descent and Collision With Terrain United Airlines Flight 585, 196 p., PDF (lire en ligne), p. 58
- ↑ Riding on Air, p. 62
- (en) Lukas Strauß et al., « Turbulence in breaking mountain waves and atmospheric rotors estimated from airborne in situ and Doppler radar measurements », Quarterly Journal of the Royal Meteorological Society, vol. 141, no 693, , p. 3215 (DOI 10.1002/qj.2604, lire en ligne [PDF])
- ↑ Riding on Air, p. 60
- ↑ Theory of mountain waves, p. 132
- ↑ (en)Vanda Grubišić et Brian J. Billings, « Sierra Rotors: A comparative study of three mountain wave and rotor events », Proceedings of the 12th Conference on Mountain Meteorology, American Meteorological Society, (lire en ligne [PDF], consulté le )
- ↑ (en)Vanda Grubišić et Brian J. Billings, « The Intense Lee-Wave Rotor Event of Sierra Rotors IOP 8 », Journal of the atmospheric sciences, American Meteorological Society, vol. 64, , p. 4178-4201 (lire en ligne, consulté le )
Voir aussi
Bibliographie
- [Danse avec le vent] Jean-Marie Clément, Danse avec le vent, TopFly, , 304 p. (ISBN 978-88-903432-3-0)
- [Riding on Air] (en) Rolf Hertenstein, Riding on Air, Ridge, Wave & Convergence lift, Soaring books & supplies, , 104 p.
- [Article de Kuettner] (en) Joachim Kuettner, « The rotor flow in the lee of mountains », GRD research notes, Geophysical research directorate US Air Force, no 6, (lire en ligne [PDF])
- [Types of rotors] (en) Rolf Hertenstein, « Rotor types associated with steep lee topography: Influence of the wind profile », Tellus, Blackwell Muskgaard, no 57A, (lire en ligne)
- [Expérience T-REX] (en) James Doyle, et al., « Observations and Numerical Simulations of Subrotor Vortices during T-REX », Journal of the atmospheric sciences, American meteorological society, no 66, (lire en ligne)
- [Theory of mountain waves] (en) Richard Scorer, « Theory of mountain waves of large amplitude », Quarterly Journal of the Royal Meteorological Society, vol. 85, no 364, (DOI 10.1002/qj.49708536406)














































