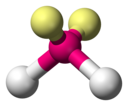
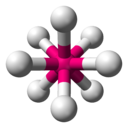
Théorie VSEPR
La théorie VSEPR (sigle de l'anglais Valence Shell Electron Pair Repulsion, en français RPECV : « répulsion des paires électroniques de la couche de valence ») est une méthode destinée à prédire la géométrie des molécules en s'appuyant sur la théorie de la répulsion des électrons de la couche de valence. Elle est aussi connue sous le nom de « théorie de Gillespie » (ou théorie de Nyholm-Gillespie).
Origines
Ce sont les Britanniques Nevil Sidgwick et Herbert Powell de l'Université d'Oxford qui ont proposé en 1940 une corrélation entre la géométrie moléculaire et le nombre des électrons de valence. En 1957 à University College de Londres, Ronald Gillespie et Ronald Sydney Nyholm se sont appuyés sur cette idée pour proposer une théorie plus détaillée. En 1958 Gillespie déménage à Université McMaster en Ontario et continue à développer et raffiner la théorie, de sorte qu'il est considéré comme le véritable instaurateur de cette théorie. La méthode VSEPR s'inscrit dans la poursuite des idées sur les liaisons chimiques de G.N. Lewis (1916).
Prérequis et supposition
La méthode VSEPR est fondée sur un certain nombre de suppositions, notamment concernant la nature des liaisons entre atomes :
- les atomes dans une molécule sont liés par des paires d'électrons ;
- deux atomes peuvent être liés par plus d'une paire d'électrons. On parle alors de liaisons multiples ;
- certains atomes peuvent aussi posséder des paires d'électrons qui ne sont pas impliqués dans une liaison. On parle de doublets non liants ;
- les électrons composant ces doublets liants ou non liants exercent les uns sur les autres des forces électriques répulsives. Les doublets sont donc disposés autour de chaque atome de façon à minimiser les valeurs de ces forces ;
- les doublets non liants occupent plus de place que les doublets liants ;
- les liaisons multiples prennent plus de place que les liaisons simples.
Notations AXE
Dans la suite de cet article, et suivant les usages de la méthode VSEPR, on notera l'atome central de la molécule étudiée A.
Les atomes liés à l'atome central A seront notés X. Le nombre de ces atomes sera noté n, qu'ils soient liés par des liaisons simples ou bien par des liaisons multiples.
Les doublets non-liants, c'est-à-dire les paires d'électrons appartenant à l'atome central A et n'étant pas impliqués dans les liaisons seront notés E et m leur nombre.
Les atomes aux molécules simples, dont la géométrie est facilement définissable grâce à la méthode VSEPR sont donc de la forme : AXnEm
À titre d'exemples, chaque atome de carbone de l'éthylène (H2C=CH2) est lié à trois autres atomes et ne possède aucun doublet libre, alors il est désigné AX3 (ou AX3E0). Et l'atome de soufre du chlorure de thionyle (SOCl2) est lié à un atome d'oxygène (par une liaison double) et deux atomes de chlore, et possède en plus un doublet libre de sorte qu'il est désigné AX3E.
Figures de répulsion
Méthode AXE
La méthode AXE permet de définir les figures suivantes. Les géométries moléculaires sont nommées selon les positions atomiques seulement et non la disposition des électrons. Par exemple, la description de AX2E2 comme molécule coudée signifie que les trois atomes AX2 ne sont pas dans une ligne droite, même si les doublets libres aident à déterminer la géométrie.
| Type | Géométrie | Exemples |
|---|---|---|
| AX1E0 (AX1) | Linéaire | HF |
| AX1E1 | Linéaire | CN− |
| AX1E2 | Linéaire | O2 |
| AX1E3 | Linéaire | HCl |
| AX2E0 (AX2) | Linéaire | BeCl2, CO2 |
| AX2E1 | Coudée | SO2, O3 |
| AX2E2 | Coudée | H2O |
| AX2E3 | Linéaire | KrF2, XeF2 |
| AX3E0 (AX3) | Trigonale plan | BF3, AlCl3 |
| AX3E1 | Pyramide trigonale | NH3 |
| AX3E2 | Forme en T | ClF3, BrF3 |
| AX4E0 (AX4) | Tétraèdre | CH4 |
| AX4E1 | Balançoire à bascule | SF4 |
| AX4E2 | Carré (plan) | XeF4 |
| AX5E0 (AX5) | Bipyramide trigonale | PCl5 |
| AX5E1 | Pyramide à base carrée | BrF5 |
| AX6E0 (AX6) | Octaèdre | SF6 |
| AX6E1 | Pyramide pentagonale | XeOF5− |
| AX7E0 (AX7) | Bipyramide pentagonale | IF7 |
| AX5E2 | Pentagone (plan) | XeF5− |
| AX8E0 (AX8) | Antiprismatique carrée | [XeF8]2− |
Géométrie
Modélisations bidimensionnelles
| Nombre stérique m+n |
Géométrie de base 0 doublet non-liant m=0 |
1 doublet non-liant m=1 |
2 doublets non-liants m=2 |
3 doublets non-liants m=3 |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |  |
 |
 |
|
| 4 | 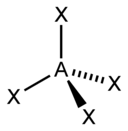 |
 |
 |
 |
| 5 |  |
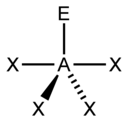 |
 |
 |
| 6 | 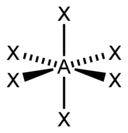 |
 base carrée |
 |
|
| 7 |  |
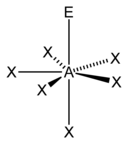 |
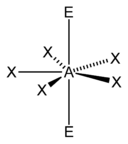 |
|
| 8 |
Modélisations tridimensionnelles
Les doublets non liants sont en jaune clair.
Améliorations du modèle
Longueur des liaisons
Jusqu'ici, nous avons considéré que les liaisons entre atomes étaient toutes de la même longueur, approximation grossière et bien éloignée de la réalité. En effet, les longueurs des liaisons varient en fonction des atomes impliqués et de la typologie de la liaison (liaison simple, liaison double, liaison triple, liaison aromatique…)
Il est possible de déterminer la distance séparant deux atomes de façon expérimentale, bien que celle-ci ne soit pas constante et dépende du milieu. On peut cependant définir une valeur moyenne.
Méthode avec les rayons de covalence
En première approximation, on pourra assimiler les atomes à des sphères dont le rayon est égal au rayon de covalence. La longueur d'une liaison sera alors donnée par la somme des rayons de covalence des atomes impliqués :
avec le rayon de covalence du premier atome et le rayon de covalence du second atome impliqué.
Méthode tenant compte de la différence d'électronégativité
Les atomes ayant chacun une électronégativité différente, cela influe aussi sur la longueur des liaisons ; plus particulièrement, une forte différence d'électronégativité implique un raccourcissement important de la liaison. On peut donc établir la formule (empirique) suivante :
avec le rayon de covalence du premier atome (en picomètres) et le rayon de covalence du second atome impliqué (en picomètres), étant la différence d'électronégativité entre les deux atomes (suivant l'échelle de Pauling).
Influence des liaisons multiples
Les formules ci-dessus permettent de calculer avec un taux d'erreur relativement faible les longueurs des liaisons simples. À partir de ces mesures, on peut facilement obtenir celles des liaisons multiples.
Une liaison double fait en moyenne, 86 % de la longueur d'une liaison simple. Une liaison triple fait en moyenne, 78 % de la longueur d'une liaison simple.
Les liaisons aromatiques telles que celles présentes dans la molécule de benzène, par exemple, sont intermédiaires entre des liaisons simples et des liaisons doubles :
- rayon de covalence du carbone : 77 pm[réf. nécessaire][1];
- longueur d'une liaison carbone-carbone simple (calculée) : 154 pm ;
- longueur d'une liaison carbone-carbone double (calculée) : 133 pm ;
- longueur des liaisons carbone-carbone dans la molécule de benzène (expérimentales) : 140 pm [2].
Limites du modèle
Même si la méthode VSEPR permet de prévoir de façon satisfaisante la géométrie de molécules simples pour lesquelles le choix d'un atome central est aisé, elle reste plus difficile à appliquer et insuffisante lorsqu'il s'agit de prévoir la géométrie de molécules plus complexes. Par exemple, tous les atomes de la molécule d'éthylène (CH2=CH2) sont situés dans un même plan, ce qu'il n'est pas possible de prévoir avec le modèle [réf. nécessaire]. Des modèles plus avancés permettent de pallier ces lacunes comme la théorie des orbitales moléculaires.
De plus, les molécules, les atomes, les électrons, les nucléons ne sont pas des structures fixes dans le temps et dans l'espace. Leurs positions relatives varient au cours du temps et suivant le milieu (voir spectroscopie infrarouge - électron). Il faut comprendre que cette théorie est simpliste par rapport à la chimie quantique et la chimie numérique.
Notes et références
- Sargent-Welch Scientifique Canada Limitée, Tableau périodique des éléments, London, Ontario,
- Bernard Valeur, Structures moléculaires, Paris, Techniques Ingénieur,
Liens externes
- (fr) « Sur la géométrie des molécules »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)
- (en) Sur la théorie VSEPR sur le site de l'Université de Sheffield