Tourbillon de Burgers

En dynamique des fluides, le tourbillon de Burgers ou toubillon de Burgers–Rott est une solution exacte des équations de Navier-Stokes dans un écoulement incompressible. Il est ainsi nommé d'après Johannes Martinus Burgers^[1] et Nicholas Rott^[2]. Il décrit un écoulement stationnaire auto-similaire en point d'arrêt en symétrie cylindrique où l'écoulement radial tend à concentrer le toubillon dans une colonne étroite autour de l'axe de symétrie tandis qu'un étirement axial provoque l'augmentation du diamètre. En même temps la dissipation visqueuse tend à étendre le tourbillon. Le tourbillon de Burgers stationnaire apparaît lorsque les trois effets sont en équilibre.

Le tourbillon de Burgers, en plus de servir d'illustration du mécanisme d'étirement tourbillonnaire peut décrire des écoulements tels que des tornades, où la vorticité est alimentée par la convection.

L'écoulement est décrit dans des coordonnées cylindriques ${\displaystyle (r,\theta ,z)}$. En supposant une symétrie axiale (pas de dépendance à ${\displaystyle \theta }$), le champ d'écoulement associé à l'écoulement axisymétrique de point d'arrêt s'écrit :

${\displaystyle v_{r}=-\alpha r}$

${\displaystyle v_{z}=2\alpha z}$

${\displaystyle v_{\theta }={\frac {\Gamma }{2\pi r}g(r)}$

où le taux de déformation ${\displaystyle \alpha >0}$ et la circulation de la vitesse ${\displaystyle \Gamma >0}$ sont donnés (paramètres du problème). L'écoulement satisfait l'équation de continuité par les deux premières équations ci-dessus. L'équation de conservation de quantité de mouvement azimutale se réduit alors à^[3] :

${\displaystyle r{\frac {d^{2}g}{dr^{2}+\left({\frac {\alpha r^{2}{\nu }-1\right){\frac {dg}{dr}=0}$

où ${\displaystyle \nu }$ est la viscosité cinématique du fluide. L'équation est intégrée avec la condition ${\displaystyle g(\infty )=1}$ de sorte qu'à l'infini la solution se comporte comme un écoulement potentiel. Le choix ${\displaystyle g(0)=0}$ garantit ${\displaystyle v_{\theta }=0}$ sur l'axe. La solution est :

${\displaystyle g=1-\exp \left(-{\frac {\alpha r^{2}{2\nu }\right)}$

L'équation de vorticité ne donne qu'une composante non triviale dans la direction ${\displaystyle z}$, donnée par :

${\displaystyle \omega _{z}={\frac {\alpha \Gamma }{2\pi \nu }\exp \left(-{\frac {\alpha r^{2}{2\nu }\right)}$

Intuitivement, l'écoulement peut être compris en regardant les trois termes de l'équation de vorticité pour ${\displaystyle \omega _{z}$ :

${\displaystyle -\alpha r{\frac {d\omega _{z}{dr}=2\alpha \omega _{z}+{\frac {\nu }{r}{\frac {d}{dr}\left(r{\frac {d\omega _{z}{dr}\right)}$

Le premier terme du côté droit de l'équation ci-dessus correspond à l'étirement du tourbillon qui intensifie la vorticité du noyau du tourbillon en raison de la composante de vitesse axiale ${\displaystyle v_{z}=2\alpha z}$. Cette vorticité tente de se diffuser radialement vers l'extérieur en raison du deuxième terme du côté droit, mais est empêchée par la convection de vorticité radiale due à ${\displaystyle v_{r}=-\alpha r}$ présent du côté gauche de l'équation ci-dessus. L'équilibre des trois mécanismes conduit à une solution stable^[4].

L'une des propriétés importantes du tourbillon de Burgers est que le taux de dissipation visqueuse total ${\displaystyle \Phi }$ par unité de longueur axiale est indépendant de la viscosité, indiquant que la dissipation est non nulle même dans la limite ${\displaystyle \nu \to 0}$. Pour cette raison, il sert de candidat approprié pour la modélisation et la compréhension des tubes tourbillonnaires étirés observés dans les écoulements turbulents. Le taux de dissipation total par unité de longueur axiale est égal à l'enstrophie totale par unité de longueur, qui est donnée par^[5] :

${\displaystyle \Phi =\nu \int _{0}^{2\pi }\int _{0}^{\infty }\omega _{z}^{2}\,rdrd\theta ={\frac {\alpha \Gamma ^{2}{4\pi }$

Une solution exacte des équations de Navier-Stokes dépendantes du temps pour une fonction arbitraire ${\displaystyle \alpha =\alpha (t)}$ peut être obtenue. En particulier, lorsque ${\displaystyle \alpha }$ est constant, le champ de vorticité ${\displaystyle \omega (r,t)}$ avec une distribution initiale arbitraire ${\displaystyle \Omega (r)=\omega (r,0)}$ est donné par^[6] :

${\displaystyle \omega (r,t)={\frac {\alpha }{2\pi \nu (1-e^{-2\alpha t})}\iint \Omega \left({\sqrt {\xi _{1}^{2}+\eta _{1}^{2}~\right)\exp \left[{\frac {-(x-\xi _{1}e^{-\alpha t})^{2}-(y-\eta _{1}e^{-\alpha t})^{2}{(2\nu /\alpha )(1-e^{-2\alpha t})}\right]\,d\xi _{1}d\eta _{1}$

Lorsque ${\displaystyle t\rightarrow \infty }$, le comportement asymptotique est donné par :

${\displaystyle \omega (r,t)={\frac {\alpha }{2\pi \nu }\exp \left(-{\frac {\alpha r^{2}{2\nu }\right)\left[\Gamma +e^{-2\alpha t}\int _{0}^{\infty }\Omega (s)\left({\frac {\alpha r^{2}{2\nu }-1\right)\left({\frac {\alpha s^{2}{2\nu }-1\right)2\pi s\,ds+O(e^{-4\alpha t})\right],\qquad \Gamma =\int _{0}^{\infty }\Omega (s)2\pi s\,ds}$

Ainsi, à condition que ${\displaystyle \Gamma \neq 0}$, une distribution de vorticité arbitraire tend vers le tourbillon de Burgers^[7]. Si ${\displaystyle \Gamma =0}$, par exemple dans le cas où la condition initiale est composée de deux tourbillons égaux et opposés, alors le premier terme est nul et le second terme implique que la vorticité décroît jusqu'à zéro lorsque ${\displaystyle t\rightarrow \infty }$.

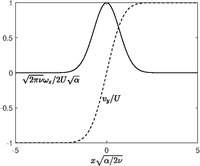
La couche tourbillonnaire ou nappe de tourbillon de Burgers est une couche de cisaillement contrainte qui est un analogue bidimensionnel plan du tourbillon de Burgers. C'est également une solution exacte des équations de Navier–Stokes, décrites pour la première fois par Albert Townsend en 1951^[8]. Le champ de vitesse ${\displaystyle (v_{x},v_{y},v_{z})}$ exprimé dans les coordonnées cartésiennes est :

${\displaystyle v_{x}=-\alpha x}$

${\displaystyle v_{z}=\alpha z}$

${\displaystyle v_{y}=U\operatorname {erf} \left({\frac {\sqrt {\alpha }x}{\sqrt {2\nu }\right)}$

où ${\displaystyle \alpha >0}$ est le taux de déformation, ${\displaystyle v_{y}(+\infty )=U}$ et ${\displaystyle v_{y}(-\infty )=-U}$. La valeur ${\displaystyle 2U}$ est interprétée comme la force de la nappe tourbillonnaire. L'équation de vorticité ne donne qu'une composante non triviale dans la direction ${\displaystyle z}$ :

${\displaystyle \omega _{z}=2U{\sqrt {\frac {\alpha }{2\pi \nu }\exp \left(-{\frac {\alpha x^{2}{2\nu }\right)}$

K. N. Beronov et S. Kida ont montré que la nappe tourbillonnaire de Burgers est instable^[9] subissant ainsi d'abord une instabilité de Kelvin-Helmholtz suivie d'autres instabilités^[10],[11] et peut être en transition vers des tourbillon de Kerr–Dold à des nombres de Reynolds modérément élevés, mais devenant pleinement turbulente pour des nombres de Reynolds élevés.

Les tourbillons de Burgers non axisymétriques apparaissent dans les écoulements contraints non axisymétriques. Leur existence pour les petits nombres de Reynolds ${\displaystyle Re=\Gamma /(2\pi \nu )}$ a été établie par A. C. Robinson et Philip Saffman en 1984^[4] tandis que Keith Moffatt, S. Kida et K. Ohkitani ont développé la théorie pour ${\displaystyle Re\gg 1}$ en 1994^[12]. La structure des tourbillons de Burgers non axisymétriques pour des valeurs arbitraires du nombre de Reynolds tourbillonnaire peut être discutée par le biais d'intégrations numériques^[13]. Le champ de vitesse prend la forme :

${\displaystyle v_{x}=-\alpha x+u(x,y)}$

${\displaystyle v_{y}=-\beta y+v(x,y)}$

${\displaystyle v_{z}=\gamma z}$

avec ${\displaystyle \gamma =\alpha +\beta }$. Sans perte de généralité, on suppose ${\displaystyle \alpha >0}$ et ${\displaystyle \gamma >0}$. La section transversale du tourbillon se situe dans le plan ${\displaystyle xy}$, ce qui donne une composante de vorticité non nulle dans la direction ${\displaystyle z}$ :

${\displaystyle \omega _{z}={\frac {\partial u}{\partial y}-{\frac {\partial v}{\partial x}$

Le tourbillon de Burgers axisymétrique est récupéré lorsque ${\displaystyle \alpha =\beta =\gamma /2}$ tandis que la couche de tourbillon de Burgers est récupérée lorsque ${\displaystyle \alpha =\gamma }$ et ${\displaystyle \beta =0}$.

La solution explicite en géométrie cylindrique avec source sur l'axe z de rayon ${\displaystyle r_{s}\geq 0}$ a été résolue par Prabakaran Rajamanickam et Adam D. Weiss^[14]. La solution est exprimée dans le système de coordonnées cylindriques s'écrit :

${\displaystyle v_{r}=-\alpha \left(r-{\frac {r_{s}^{2}{r}\right)}$

${\displaystyle v_{z}=2\alpha z}$

${\displaystyle v_{\theta }={\frac {\Gamma }{2\pi r}P\left(1+{\frac {\alpha r_{s}^{2}{2\nu },{\frac {\alpha r^{2}{2\nu }\right)}$

où ${\displaystyle \alpha >0}$ est le taux de déformation, ${\displaystyle \Gamma >0}$ est la circulation de la vitesse et ${\displaystyle P}$ est la fonction gamma incomplète. Cette solution n'est autre que le tourbillon de Burgers en présence d'un source linéaire avec une intensité de source ${\displaystyle Q=2\pi \alpha r_{s}^{2}$. L'équation de vorticité ne donne qu'une composante non triviale dans la direction ${\displaystyle z}$, donnée par :

${\displaystyle \omega _{z}={\frac {\alpha \Gamma }{2\pi \nu {\tilde {\Gamma }(1+\alpha r_{s}^{2}/2\nu )}\left({\frac {\alpha r^{2}{2\nu }\right)^{\alpha r_{s}^{2}/2\nu }\exp \left(-{\frac {\alpha r^{2}{2\nu }\right)}$

où ${\displaystyle {\tilde {\Gamma }$ dans l'expression ci-dessus est la fonction gamma. Lorsque ${\displaystyle r_{s}\rightarrow 0}$, la solution se réduit à la solution du toubillon de Burgers et lorsque ${\displaystyle r_{s}\rightarrow \infty }$ la solution devient la solution de la couche tourbillonnaire de Burgers.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Burgers vortex » (voir la liste des auteurs).

• Portail de la physique