1 + 2 + 3 + 4 + ⋯

A serie infinita cuxos termos son os números naturais 1 + 2 + 3 + 4 + ⋯ é unha serie diverxente. A n- ésima suma parcial da serie é o número triangular
que aumenta sen límite cando n vai ao infinito. Debido a que a secuencia de sumas parciais non consegue converxer a un límite finito, a serie non ten unha suma.
En matemáticas úsanse moitos métodos de suma para asignar valores numéricos mesmo a unha serie diverxente. En particular, os métodos de regularización da función zeta e a suma de Ramanujan asignan á serie un valor de− 1/12 que se expresa mediante unha famosa fórmula:[2]
onde o valor obtido debe ser interpretado como o valor obtido mediante un dos métodos de suma mencionados anteriormente e non como a suma dunha serie infinita no seu significado habitual. Estes métodos teñen aplicacións noutros campos como a análise complexa, a teoría cuántica de campos e a teoría de cordas.
Sumas parciais
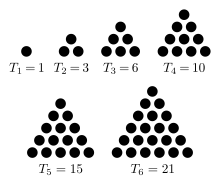
As sumas parciais da serie 1 + 2 + 3 + 4 + 5 + 6 + ⋯ son 1, 3, 6, 10, 15, etc. A n-ésima suma parcial vén dada por unha fórmula sinxela:
Esta ecuación era coñecida polos pitagóricos xa no século VI a.C.[3] Os números desta forma chámanse números triangulares, porque poden ordenarse como un triángulo equilátero.
Sumabilidade

Srinivasa Ramanujan presentou dúas deducións de " 1 + 2 + 3 + 4 + ⋯ = − 1/12 no capítulo 8 do seu primeiro caderno.[4][5][6]
Baseado na serie alternada
A primeira idea clave é que a serie de números positivos 1 + 2 + 3 + 4 + ⋯ parécese moito á serie alternada 1 − 2 + 3 − 4 + ⋯. Esta última serie tamén é diverxente, mais é moito máis doado de traballar; existen varios métodos clásicos que lle atribúen un valor, que se exploran dende o século XVIII.[7]
A segunda idea clave é que a serie alternada 1 − 2 + 3 − 4 + ⋯ é a expansión formal da serie de potencias (para x no punto 0) da función que é avaliada para . En consecuencia, Ramanujan escribe
Dividindo ambos os dous lados por −3, obtense .
Regularización da función zeta

Na regularización da función zeta, a serie substitúese pola serie Esta última serie é un exemplo dunha serie de Dirichlet. Cando a parte real de s é maior que 1, a serie de Dirichlet converxe, e a súa suma é a función zeta de Riemann ζ(s). Por outra banda, a serie de Dirichlet diverxe cando a parte real de s é menor ou igual a 1, polo que, en particular, a serie 1 + 2 + 3 + 4 + ⋯ que resulta de estabelecer s = −1 non converxe. O beneficio de introducir a función zeta de Riemann é que se pode definir para outros valores de s mediante a continuación analítica. Pódese entón definir a suma zeta-regularizada de 1 + 2 + 3 + 4 + ⋯ como ζ (−1).
A partir deste punto, hai algunhas formas de demostrar que ζ(−1) = − 1/12.
A identidade séguese cumprindo cando ambas as funcións se estenden mediante o prolongamento analítico para incluír valores de s para os que diverxen as series anteriores. Substituíndo s = −1, obtense −3ζ(−1) = η(−1). Agora, calcular η(−1) é unha tarefa máis sinxela, xa que a función eta é igual á suma de Abel da serie que a define,[8] que é un límite unilateral:
Dividindo ambos os dous lados por −3, obtense
Sumatorio de Ramanujan
A suma Ramanujan de 1 + 2 + 3 + 4 + ⋯ tamén é − 1/12. Está recollido nunha carta que envía a G. H. Hardy, no 27 de febreiro de 1913.
A suma de Ramanujan é un método para illar o termo constante na fórmula de Euler-Maclaurin para as sumas parciais dunha serie. Para unha función f, a suma clásica de Ramanujan da serie defínese como
onde f(2k−1) é a (2k − 1)-ésima derivada de f e B2k é o (2k)-ésimo número de Bernoulli: B2 = 1/6, B4 = − 1/30, etc. Facendo f(x) = x, a primeira derivada de f é 1, e todos os demais termos desaparecen, polo que[9]
Para evitar inconsistencias, a teoría moderna do sumatorio de Ramanujan require que f sexa "regular" no sentido de que as derivadas de orde superior de f decaen o suficientemente rápido como para que os termos restantes na fórmula de Euler-Maclaurin tenden a 0. Ramanujan asumiu tácitamente esta propiedade. O requisito de regularidade impide o uso da suma Ramanujan en series espaciadas como 0 + 2 + 0 + 4 + ⋯, porque ningunha función regular toma eses valores. Pola contra, tal serie debe interpretarse mediante a regularización da función zeta. Por este motivo, Hardy recomenda "gran precaución" ao aplicar as sumas Ramanujan das series coñecidas para atopar as sumas das series relacionadas.[10]
Notas
- ↑ Tao, Terence (April 10, 2010). The Euler–Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation. Consultado o January 30, 2014..
- ↑ Lepowsky, J. (1999). "Vertex operator algebras and the zeta function". En Naihuan Jing and Kailash C. Misra. Recent Developments in Quantum Affine Algebras and Related Topics. Contemporary Mathematics 248. pp. 327–340. Bibcode:1999math......9178L. arXiv:math/9909178..
- ↑ Pengelley, David J. (2002). "The bridge between the continuous and the discrete via original sources". En Otto Bekken; et al. Study the Masters: The Abel-Fauvel Conference. National Center for Mathematics Education, University of Gothenburg, Sweden. p. 3. ISBN 978-9185143009.
- ↑ Ramanujan's Notebooks. Consultado o January 26, 2014.
- ↑ Abdi, Wazir Hasan (1992). Toils and triumphs of Srinivasa Ramanujan, the man and the mathematician. National. p. 41.
- ↑ Berndt, Bruce C. (1985). Ramanujan's Notebooks: Part 1. Springer-Verlag. pp. 135–136.
- ↑ Euler, Leonhard (2006). "Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series". Traducido por Willis, Lucas; Osler, Thomas J. The Euler Archive. Consultado o 2007-03-22. Orixinalmente publicado como Euler, Leonhard (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques". Mémoires de l'Académie des Sciences de Berlin 17: 83–106.
- ↑ Knopp, Konrad (1990) [1922]. Theory and Application of Infinite Series. Dover. pp. 490–492. ISBN 0-486-66165-2.
- ↑ Berndt, Bruce C. (1985). Ramanujan's Notebooks: Part 1. Springer-Verlag. pp. 13, 134..
- ↑ Hardy 1949, p. 346.
Véxase tamén
Bibliografía
- Berndt, Bruce C.; Srinivasa Ramanujan Aiyangar; Rankin, Robert A. (1995). Ramanujan: letters and commentary. American Mathematical Society. ISBN 0-8218-0287-9.
- Hardy, G. H. (1949). Divergent Series. Clarendon Press.
- Zee, A. (2003). Quantum field theory in a nutshell. Princeton UP. ISBN 0-691-01019-6.
Outros artigos
Ligazóns externas
- Lamb E. (2014), "Does 1+2+3... Really Equal –1/12?", Scientific American Blogs.
- This Week's Finds in Mathematical Physics (Week 124), (Week 126), (Week 147), (Week 213)
- Euler's Proof That 1 + 2 + 3 + ⋯ = −1/12 – by John Baez
- John Baez (September 19, 2008). "My Favorite Numbers: 24" (PDF).
- The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation by Terence Tao
- A recursive evaluation of zeta of negative integers by Luboš Motl
- Suma de números naturais (segunda proba e imaxes extra) inclúe unha demostración do método de Euler.
- Why –1/12 is a gold nugget vídeo de seguimento de Numberphile de Edward Frenkel
- Divergent Series: why 1 + 2 + 3 + ⋯ = −1/12 por Brydon Cais daUniversity of Arizona

















