המשולש הישר של פרמה
המשולש הישר של פרמה הוא שמה של הוכחת אי-קיום בתורת המספרים, שפורסמה בשנת 1670 יחד עם יצירותיו של פייר דה פרמה, זמן קצר לאחר מותו. זו ההוכחה השלמה היחידה הידועה לנו שכתב פרמה[1]. יש לה כמה ניסוחים שווים, שאחד מהם נאמר (אך לא הוכח) כ-450 שנה לפני פרמה, בשנת 1225 על ידי פיבונאצ'י. בצורותיו הגאומטריות, הוא קובע:
- משולש ישר-זווית במישור האוקלידי שכל שלושת אורכי הצלעות שלו הם מספרים רציונליים לא יכול להיות בעל שטח שהוא הריבוע של מספר רציונלי. השטח של משולש ישר-זווית רציונלי נקרא מספר קונגרואנטי, כך שאף מספר קונגרואנטי מרובע.
- משולש ישר-זווית וריבוע עם שטחים שווים לא יכולים להיות בעלי מידה משותפת בכל צדדיהם.
- אין שני משולשים ישרי זווית פיתגוריים שבהם שתי הרגליים של משולש אחד הן הרגל והיתר של המשולש השני.
באופן מופשט יותר, כתוצאה מכך לגבי משוואות דיופנטיות (פתרונות שלמים או מספרים רציונליים למשוואות פולינומיות), היא שווה ערך לאמירות ש:
- אם שלושה מספרים ריבועיים יוצרים סדרה חשבונית, הרי שהפער בין מספרים עוקבים בסדרה (הנקרא הפרש או קונגרואום) אינו יכול להיות בעצמו ריבועי.
- הנקודות הרציונליות היחידות בעקומה האליפטית הן שלוש הנקודות הטריוויאליות עם ו .
- למשוואה מהמעלה הרביעית אין פתרון שלם שאינו אפס.
תוצאה מיידית של הניסוח האחרון לעיל היא שהמשפט האחרון של פרמה נכון במקרה המיוחד שמעריכו הוא 4.
ייצוגים ונסחים שונים
ריבועים בסדרה חשבונית
שטחים של משולשים ישרי זווית
מכיוון שהקונגרואה הם מספרים שהם בדיוק פי ארבעה מהשטח של שלשה פיתגורית, והכפלה בארבע אינה משנה את תכונת הריבועית, קיומו של קונגרום מרובע מקבילה לקיומו של שלשה פיתגורית עם שטח ריבועי. גרסה זו של הבעיה נוגעת להוכחת פרמה: הוא מראה שאין משולש כזה. בהתחשב בבעיה זו, פרמה לא קיבל השראה מפיבונאצ'י אלא ממהדורה של אריתמטיקה מאת דיופנטוס, שפורסמה בתרגום לצרפתית בשנת 1621 על ידי קלוד גאספר בשה דה מזריאק.[2] ספר זה תיאר משולשים ישרי זווית מיוחדים אשר בשטחים שלהם היו צורות הקשורות לריבועים, אך לא התייחס למקרה של שטחים שהם עצמם ריבועיים.[3]
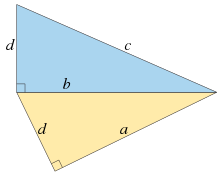
על ידי סידור מחדש של המשוואות לשני המשולשים הפיתגוריים למעלה, ולאחר מכן הכפלתם יחד, מתקבלת המשוואה הדיופנטית היחידהאשר ניתן לפשט על ידי הצגת משתנה חדש ללעומת זאת, כל שלושה מספרים שלמים חיוביים המצייתים למשוואה מובילים לקונגרום מרובע: למספרים אלה, הריבועים , , ו יוצרים התקדמות אריתמטית עם קונגרום , שהוא ריבועי בעצמו. לפיכך, הפתרון של שווה לקיומו של קונגרום מרובע. אבל, אם למשפט האחרון של פרמה הייתה דוגמה נגדית במעריך , פתרון שלם למשוואה , ואז ריבוע אחד משלושת המספרים בזוגמה הנגדית ייתן שלושה מספרים הפותרים את המשוואה . לכן ההוכחה של פרמאט כי אין למשולש פיתגורס שטח מרובע מרמזת על נכונות של מקרה המעריך- של המשפט האחרון של פרמה.[7]
ניסוח שווה ערך אחר של אותה בעיה כולל מספרים קונגריואנטיים, המספרים שהם שטחים של משולשים ישרי זווית שכל שלוש הצלעות שלהם הם מספרים רציונליים . על ידי הכפלת הצלעות במכנה משותף, כל מספר תואם עשוי להפוך לשטח של משולש פיתגורי, ומכאן יוצא שהמספרים הקונגרואנטיים הם בדיוק המספרים הנוצרים על ידי הכפלת קונוגרום בריבוע של מספר רציונלי. לכן, קיומו של קונגרום מרובע מקביל לאמירה כי המספר 1 אינו מספר קונגרואנטי. דרך גאומטרית נוספת לקביעת ניסוח זה היא שלא ייתכן כי ריבוע (הצורה הגאומטרית) ומשולש ישר-זווית יהיו שני שטחים שווים וכל הצלעות תואמות זו לזו.[10]
עקומה אליפטית

צורה מקבילה נוספת של משפט פרמה כוללת עקומה אליפטית המורכבת מנקודות אשר הקואורדינטות הקרטזיות מקיימות את המשוואה:הנקודות (1,0−), (0,0) ו- (1,0) מספקות פתרונות ברורים למשוואה זו. משפט פרמה שקול לאמירה כי אלה הנקודות היחידות בעקומה שעבורן ו הם רציונליים. באופן כללי יותר, המשולשים ישרי הזווית עם צלעות רציונליים ושטח מתאימות אחד לאחד עם הנקודות הרציונליות עם קואורדינטת חיובית על העקומה האליפטית .[4][5]
ההוכחה של פרמה
במהלך חייו אתגר פרמה מתמטיקאים אחרים שיוכיחו את אי-קיומו של משולש פיתגורי עם שטח ריבועי, אך לא פרסם את ההוכחה בעצמו. עם זאת, הוא כתב הוכחה בעותק שלו של "אריתמטיקה" (של דיופנטוס), אותו העתק שבו כתב שהוא יכול להוכיח את המשפט האחרון של פרמה. בנו של פרמה קלמנט-סמואל פרסם מהדורה של ספר זה, הכולל את הערות השוליים של פרמה עם הוכחת משפט המשולש ישר-זווית, בשנת 1670.
ההוכחה של פרמה היא הוכחה על ידי נסיגה אינסופית. הוא מראה כי מכל דוגמה של משולש פיתגורי עם שטח ריבועי ניתן להפיק דוגמה קטנה יותר. מאחר שמשולשים פיתגוריים הם בעלי שטחים שלמים חיוביים, ולא קיים רצף יורד אינסופי של מספרים שלמים חיוביים, גם לא יכול להתקיים משולש פיתגורי עם שטח ריבועי.
בפירוט רב יותר, נניח שכן , , ו הם צלעותיהם השלמות של משולש ישר-זווית עם שטח ריבועי. על ידי חלוקה בכל הגורמים המשותפים, ניתן להניח שהמשולש הוא פרימיטיבי [10] ומהצורה הידועה של כל השלשות הפיתגוריות הפרימיטיביות, אפשר להגדיר , , ו , שבאמצעותו הופכת הבעיה למציאת מספרים זרים ו (אחד מהם אי זוגי) כזה שהאזור הוא ריבועי. כדי שמספר זה יהיה ריבוע, ארבעת הגורמים הליניאריים שלו , , , ו (שהם זרים) חייבים בעצמם להיות ריבועיים; נניח ו . ו חייבים שניהם להיות אי-זוגיים, שכן בדיוק אחד מ אוֹ הוא זוגי והשני אי-זוגי. לכן, שניהם ו הם זוגיים, ואחד מהם מתחלק ב-4. חלוקתם בשניים מייצרת עוד שני מספרים שלמים ו , שאחד מהם הוא אי זוגי לפי המשפט הקודם. כי הוא ריבועי, ו הן רגלי משולש פיתגורס פרימיטיבי אחר ששטחו . משום ש הוא עצמו ריבועי וש- הוא אי זוגי, הוא ריבועי. לפיכך, כל משולש פיתגורס עם שטח ריבועי מוביל למשולש פיתגורס קטן יותר עם שטח ריבועי, המשלים את ההוכחה.
קישורים חיצוניים
- המשולש הישר של פרמה, באתר MathWorld (באנגלית)
הערות שוליים
- ^ תבנית:Harvtxt. Many subsequent mathematicians published proofs, including Gottfried Wilhelm Leibniz (1678), Leonhard Euler (1747), and Bernard Frenicle de Bessy (before 1765); see תבנית:Harvtxt and תבנית:Harvtxt.
- ^ Edwards, Harold M. (2000), "1.6 Fermat's one proof", Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory, Graduate Texts in Mathematics, vol. 50, Springer, pp. 10–14, ISBN 978-0-387-95002-0
- ^ Stillwell, John (1998), "4.7 The area of rational right triangles", Numbers and Geometry, Undergraduate Texts in Mathematics, Springer, pp. 131–133, ISBN 978-0-387-98289-2
- ^ Koblitz, Neal (1993), Introduction to Elliptic Curves and Modular Forms, Graduate Texts in Mathematics, vol. 97 (2nd ed.), Springer-Verlag, ISBN 0-387-97966-2
- ^ Kato, Kazuya; Saitō, Takeshi (2000), Number Theory: Fermat's dream, Translations of mathematical monographs, תורגם ע"י Nobushige Kurokawa, American Mathematical Society, p. 17, ISBN 978-0-8218-0863-4


















































