שער לוגי

שער לוגי הוא רכיב פיזיקלי המבצע פעולות באלגברה בוליאנית, או מודל חישובי המייצג שער אידיאלי כזה. שערים לוגיים מקבילים לקשרים לוגיים שהתפתחו בלוגיקה הפורמלית. שערים לוגיים מקובלים הם:
השער הלוגי הוא מרכיב בסיסי במעגלים אלקטרוניים דיגיטליים, וככזה הוא נמצא בבסיסם של מכשירים אלקטרוניים רבים כגון: מחשב, טלפון סלולרי, DVD, שעון דיגיטלי ועוד.
היסטוריה
הרעיון להשתמש בערכי-אמת לוגיים לצורך חישובים שונים נהגה על ידי איש האשכולות גוטפריד וילהלם לייבניץ. המערכת הבינארית נומרית הוגדרה על ידי לייבניץ כמרכיב חשוב של כל מחשב מודרני. עם זאת, עד לשנות ה-40 של המאה ה-20 הרבה תכנונים התבססו על המערכת הדצימלית הקשה בהרבה למימוש. השערים הלוגיים הראשונים היו מכניים. ב-1837 צ'ארלס בבג' תכנן את המנוע האנליטי, שהכיל שערים לוגים מכניים. ב-1891 אלמון סטראוג'ר רשם פטנט על מתקן המכיל שערים לוגים מבוססי ממסרים. התקדמות בייעול התרחשה לאחר שלודוויג ויטגנשטיין ניסח טבלת אמת של כל קשר לוגי בספרו טרקטט לוגי-פילוסופי.
המצאת שפופרת הריק והטריודה אפשרה ב-1924, לולתר בותה, את תכנון השערים הלוגיים המודרניים הראשונים[1]. המצאת הטרנזיסטור ב-1947, חוללה מהפכה באלקטרוניקה, ואפשרה יצור שערים לוגים קטנים ואמינים יותר. כיום ניתן למצוא על פיסת סיליקון אחת מיליוני שערים לוגיים, דבר המאפשר יכולות חישוב גדולות.
מבנה
שערים לוגיים ממומשים בעזרת מתגים, כאשר כיום הטרנזיסטור משמש כ"מתג אלקטרוני". למימוש שער AND מציבים שני "מתגים" בטור בין מקור המתח למוצא השער, ולמימוש שער OR מציבים שני מתגים במקביל בין מקור המתח למוצא השער. כיום השיטה הנפוצה ביותר שבה מיוצרים שערים לוגיים היא שיטת CMOS.
צירופי שערים
ניתן לממש לוגיקה בוליאנית מורכבת באמצעות צירוף של שערים לוגיים בסיסיים המפורטים לעיל. באמצעות מפת קרנו ניתן לפשט לוגיקות מורכבות, ולהגיע למימוש פשוט יותר, שבדרך כלל דורש פחות רכיבים - בהשוואה למימוש של הלוגיקה הראשונית.
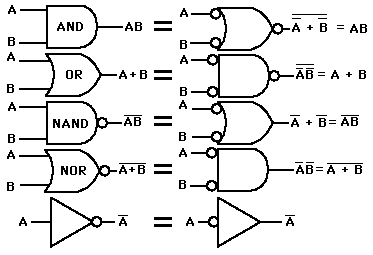
כללי דה מורגן מראים כיצד אפשר לממש שער לוגי מסוים באמצעות שערים אחרים, ובפרט הם מאפשרים להוכיח (כפי שהראה צ'ארלס פירס) כי כל אחד מהשערים הלוגיים ניתן למימוש באמצעות צירופים של שערי NAND לוגי בלבד, או באמצעות צירופים של שערי NOR לוגי בלבד.
סוגי שערים
בתרשימים אלקטרוניים מוצגים השערים בצורה הבאה:
שער AND
הפעולה הבוליאנית AND, מספקת במוצא '1' רק כאשר כל הכניסות לשער, נימצאות במצב '1'. ניתן לממש פעולה זו על ידי שני מפסקים המחוברים בטור למקור מתח. המעגל יוליך חשמל אל מוצא המעגל (אחרי 2 המפסקים) רק אם שני המפסקים יהיו במצב ON.
הטבלה הבאה מסכמת את פעולת השער הלוגי AND:
| קלט A | קלט B | פלט F |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
בתרשימים אלקטרוניים מוצג AND לוגי בצורות הבאות:
שער OR
הפעולה הבוליאנית OR מספקת במוצא '1' כאשר לפחות אחת הכניסות, במצב '1'. ניתן לממש פעולה זו על ידי שני מפסקים המחוברים במקביל למקור מתח. המעגל יוליך חשמל אל מוצא המעגל אם אחד מהמפסקים (או יותר) יהיו במצב ON.
הטבלה הבאה מסכמת את פעולת השער הלוגי OR:
| קלט A | קלט B | פלט F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
שער NOT

הפעולה האונרית NOT מספקת במוצא את ההפך מערך הכניסה. ניתן לממש פעולה זו על ידי שני מפסקים בעלי התנהגות הפוכה (במצב מסוים האחד מוליך והשני מנותק) המחוברים בטור בין מקור מתח (הנחשב ל-1 לוגי) לבין אדמה או מקור מתח אחר הנחשב ל-'0' לוגי. מוצא המעגל יהיה בין שני המפסקים. בהינתן כניסה של '1' המפסק שמחובר ל-'0' יוליך. בהינתן כניסה של '0' המפסק שמחובר ל-'1' יוליך.
בתמונה ניתן לראות מימוש שער NOT לוגי על ידי טרנזיסטורים.
טבלת האמת של הפעולה הבוליאנית 'NOT' ושל הקשר 'לא' נתונה בטבלה הבאה:
| קלט | פלט |
|---|---|
| 0 | 1 |
| 1 | 0 |

