Húrmetszetgráf
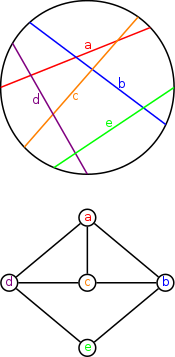
A matematika, azon belül a gráfelmélet területén egy húrmetszetgráf (circle graph) egy kör húrjainak metszetgráfja. Tehát olyan irányítatlan gráf, melynek csúcsai egy kör húrjainak felelnek meg, két csúcs között pedig akkor húzódik él, ha a csúcsoknak megfelelő húrok metszik egymást.
Számítási bonyolultság
A (Spinrad 1994) által megadott algoritmus O(n2) időben eldönti egy n csúcsú irányítatlan gráfról, hogy húrmetszetgráf-e, és ha igen, meg is konstruál egy húrhalmazt, amivel elő lehet állítani.
Számos, általános gráfokon NP-teljes problémára léteznek polinom idejű algoritmusok, ha húrmetszetgráfrokról van szó. Például (Kloks 1996) megmutatta, hogy egy húrmetszetgráf favastagsága meghatározható és egy optimális fafelbontás előállítható O(n3) időben. Ráadásul egy minimális feltöltődés (a lehető legkevesebb éllel rendelkező, az adott húrmetszetgráfot részgráfként tartalmazó merev körű gráf) is O(n3) időben előállítható.[1] (Tiskin 2010) megmutatta, hogy egy húrmetszetgráf maximális elemszámú klikkje O(n log2 n) időben megtalálható, míg (Nash & Gregg 2010) igazolta, hogy egy súlyozatlan húrmetszetgráf maximális elemszámú független halmaza O(n min{d, α}) időben megtalálható, ahol d paraméter a gráf sűrűségét, α pedig a gráf függetlenségi számát jelöli.
Néhány más probléma NP-teljes marad húrmetszetgráfokon is. Ezek közé tartoznak a minimális domináló halmaz, minimális összefüggő domináló halmaz és a minimális totálisandomináló halmaz problémái.[2]
Kromatikus szám

Egy húrmetszetgráf kromatikus száma az a minimális szám, amennyi színnel ki lehet színezni a húrokat úgy, hogy semelyik két metsző húrnak ne egyezzen a színe. Mivel egy körnek tetszőlegesen sok húrja metszheti egymást, ezért egy húrmetszetgráf kromatikus száma bármilyen nagy is lehet, a húrmetszetgráf kromatikus számának meghatározása pedig NP-teljes probléma.[3] Még annak az eldöntése is NP-teljes, hogy adott húrmetszetgráf négy színnel színezhető-e.[4] (Unger 1992) állítása szerint a 3-színezés keresése polinom időben végrehajtható, de leírásából fontos részletek hiányoznak.[5]
Többen vizsgálták annak kérdését, hogy a húrmetszetgráfok egyes osztályait lehetséges-e kevesebb színnel kiszínezni. Például az olyan húrmetszetgráfok, melyekben nincs egymást metsző k vagy több húr, a színezés lehetséges akár színnel is.[6] Abban a speciális esetben, amikor k = 3 (tehát a háromszögmentes húrmetszetgráfokban) a kromatikus szám legfeljebb öt lehet, és ez éles eredmény: minden háromszögmentes húrmetszetgráf színezhető öt színnel, és létezik olyan közöttük, melyhez szükséges is az öt szín.[7] Ha egy húrmetszetgráf bősége legalább öt (tehát háromszögmentes és nincs benne négy csúcsú kör sem), legfeljebb három színnel is kiszínezhető.[8]
Alkalmazások
A húrmetszetgráfok megjelennek a VLSI áramkörök tervezésekor is, mint a huzalozás egy speciális esetének, méghozzá a „két terminálos switchbox huzalozásnak” az absztrakt reprezentációi. Ebben az esetben a huzalozási terület téglalap, minden hálózathoz két terminál tartozik, és a terminálok a téglalap kerületén találhatók. Könnyen belátható, hogy ezeknek a hálózatoknak a metszetgráfja egy húrmetszetgráf.[9] A huzalozási lépés céljai között szerepel, hogy a különböző hálózatok elektromosan ne érintkezzenek, és a potenciálisan mégis érintkező részek más-más vezetőrétegekbe legyenek vezetve. Ezért a húrmetszetgráfokkal a huzalozási probléma különböző aspektusait lehet megragadni.
A húrmetszetgráfok színezései alkalmasak lehetnek tetszőleges gráf könyvbeágyazásának megkeresésére: ha adott G gráf csúcsait egy körön helyezzük el, élei pedig a kör húrjainak felelnek meg, akkor a húrok metszetgráfja húrmetszetgráf, melynek színezései ekvivalensek az adott köri elrendezés könyvbeágyazásával. Ebben a megfeleltetésben a színezés színeinek száma megegyezik a könyvbeágyazás lapjainak számával.[4]
Kapcsolódó gráfcsaládok
Egy gráf pontosan akkor húrmetszetgráf, ha felrajzolható egy egyenesen lévő intervallumok átfedési gráfjaként. Ez olyan gráf, melynek csúcsai az intervallumoknak felelnek meg, két csúcs pedig akkor van éllel összekötve, ha a két intervallum között van átfedés, de egyik sem tartalmazza a másikat.
A véges négyszöggráfok duálisai háromszögmentes húrmetszetgráfok.[10]
Az egyenesen lévő intervallumok metszetgráfját intervallumgráfnak nevezik.
A füzérgráfok, a síkgörbék metszetgráfjai speciális esetként tartalmazzák a húrmetszetgráfokat.
Minden távolság-örökletes gráf húrmetszetgráf, ahogy minden permutációgráf és egység-intervallumgráf is. Minden külsíkgráf is húrmetszetgráf.[11]
Fordítás
- Ez a szócikk részben vagy egészben a Circle graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
- ↑ (Kloks, Kratsch & Wong 1998).
- ↑ (Keil 1993)
- ↑ Garey et al. (1980).
- ↑ a b Unger (1988).
- ↑ Unger (1992).
- ↑ (Černý 2007). A korábban megállapított korlátokat lásd: (Gyárfás 1985), (Kostochka 1988) és (Kostochka & Kratochvíl 1997).
- ↑ Lásd (Kostochka 1988)-nál a felső korlátot és (Ageev 1996)-nál az alsót. (Karapetyan 1984) és (Gyárfás & Lehel 1985) korábban gyengébb korlátokat határozott meg ugyanerre a problémára.
- ↑ (Ageev 1999).
- ↑ Naveed Sherwani, "Algorithms for VLSI Physical Design Automation"
- ↑ Bandelt, Chepoi & Eppstein (2010).
- ↑ (Wessel & Pöschel 1985); (Unger 1988).
- Ageev, A. A. (1996), "A triangle-free circle graph with chromatic number 5", Discrete Mathematics 152 (1-3): 295–298, DOI 10.1016/0012-365X(95)00349-2.
- Ageev, A. A. (1999), "Every circle graph of girth at least 5 is 3-colourable", Discrete Mathematics 195 (1-3): 229–233, DOI 10.1016/S0012-365X(98)00192-7.
- Bandelt, H.-J.; Chepoi, V. & Eppstein, D. (2010), "Combinatorics and geometry of finite and infinite squaregraphs", SIAM Journal on Discrete Mathematics 24 (4): 1399–1440, DOI 10.1137/090760301.
- Černý, Jakub (2007), "Coloring circle graphs", Electronic Notes in Discrete Mathematics 29: 357–361, DOI 10.1016/j.endm.2007.07.072.
- Garey, M. R.; Johnson, D. S. & Miller, G. L. et al. (1980), "The complexity of coloring circular arcs and chords", SIAM. J. on Algebraic and Discrete Methods 1 (2): 216–227, DOI 10.1137/0601025.
- Gyárfás, A. (1985), "On the chromatic number of multiple interval graphs and overlap graphs", Discrete Mathematics 55 (2): 161–166, DOI 10.1016/0012-365X(85)90044-5. As cited by (Ageev 1996).
- Gyárfás, A. & Lehel, J. (1985), "Covering and coloring problems for relatives of intervals", Discrete Mathematics 55 (2): 167–180, DOI 10.1016/0012-365X(85)90045-7. As cited by (Ageev 1996).
- Karapetyan, A. (1984), On perfect arc and chord intersection graphs, Ph.D. thesis, Inst. of Mathematics, Novosibirsk. As cited by (Ageev 1996).
- Keil, J. Mark (1993), "The complexity of domination problems in circle graphs", Discrete Applied Mathematics 42 (1): 51–63, DOI 10.1016/0166-218X(93)90178-Q.
- Kloks, Ton (1996), "Treewidth of Circle Graphs", Int. J. Found. Comput. Sci. 7 (2): 111–120, DOI 10.1142/S0129054196000099.
- Kloks, T.; Kratsch, D. & Wong, C. K. (1998), "Minimum fill-in on circle and circular-arc graphs", Journal of Algorithms 28 (2): 272–289, DOI 10.1006/jagm.1998.0936.
- Kostochka, A.V. (1988), "Upper bounds on the chromatic number of graphs", Trudy Instituta Mathematiki 10: 204–226. As cited by (Ageev 1996).
- Kostochka, A.V. & Kratochvíl, J. (1997), "Covering and coloring polygon-circle graphs", Discrete Mathematics 163 (1–3): 299–305, DOI 10.1016/S0012-365X(96)00344-5.
- Nash, Nicholas & Gregg, David (2010), "An output sensitive algorithm for computing a maximum independent set of a circle graph", Information Processing Letters 116 (16): 630–634, DOI 10.1016/j.ipl.2010.05.016.
- Spinrad, Jeremy (1994), "Recognition of circle graphs", Journal of Algorithms 16 (2): 264–282, DOI 10.1006/jagm.1994.1012.
- Tiskin, Alexander (2010), "Fast distance multiplication of unit-Monge matrices.", Proceedings of ACM-SIAM SODA 2010, pp. 1287–1296.
- Unger, Walter (1988), "On the k-colouring of circle-graphs", STACS 88: 5th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux, France, February 11–13, 1988, Proceedings, vol. 294, Lecture Notes in Computer Science, Berlin: Springer, pp. 61–72, DOI 10.1007/BFb0035832.
- Unger, Walter (1992), "The complexity of colouring circle graphs", STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science, Cachan, France, February 13–15, 1992, Proceedings, vol. 577, Lecture Notes in Computer Science, Berlin: Springer, pp. 389–400, DOI 10.1007/3-540-55210-3_199.
- Wessel, W. & Pöschel, R. (1985), "On circle graphs", in Sachs, Horst, Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory Held in Eyba, October 1st to 5th, 1984, vol. 73, Teubner-Texte zur Mathematik, B.G. Teubner, pp. 207–210. As cited by (Unger 1988).
