Ionizációs energia

Az ionizációs energia – jele Ei – a fizikában és kémiában az a legkisebb energiamennyiség, amely a leggyengébben kötött elektron – a vegyértékelektron – egyedülálló, semleges atomból vagy molekulából történő eltávolításához szükséges. Képlettel leírva:
- X(g) + energia → X+(g) + e−
ahol X ionizálható atom vagy molekula, X+ az elektron eltávolításával kapott kation, e− pedig az eltávolított elektron.[1] Az elektron eltávolítása általában endoterm folyamat, jellemzően minél közelebb van a legkülső elektron az atommaghoz, annál nagyobb az ionizációs energia.
A fizikában az egyetlen elektronnak egyetlen atomból vagy molekulából történő eltávolításához szükséges energiát szokás használni, ezt elektronvolt egységben adják meg. A kémiában jellemzően egy mól anyagra vonatkoztatott mennyiséget, moláris ionizációs energiát vagy entalpiát használnak, ennek mértékegysége kJ/mol.[2]
A kémiai elemek periódusos rendszerében összehasonlítva az Ei értékeket két trend fedezhető fel:
- egy perióduson (soron) belül balról jobbra haladva Ei értéke jellemzően növekszik
- egy csoporton (oszlopon) belül lefelé haladva Ei értéke jellemzően csökken.
Az utóbbi tendencia annak a következménye, hogy az oszlopban lefelé haladva periódusonként eggyel több belső elektronhéj van, így a legkülső elektronhéj egyre távolabb kerül az atommagtól.
Az n-edik ionizációs energia az (n−1) töltésű részecskéből egy elektronnak az eltávolításához szükséges energiája. Az első három ionizációs energia definíciója például a következő:
- 1. ionizációs energia
- X → X+ + e−
- 1. ionizációs energia
- 2. ionizációs energia
- X+ → X2+ + e−
- 2. ionizációs energia
- 3. ionizációs energia
- X2+ → X3+ + e−
- 3. ionizációs energia
Az ionizációs potenciál az ionizációs energia régebbi elnevezése,[3] a legrégebbi módszer szerint az ionizációs energiát ugyanis úgy mérték, hogy ionizálták a mintát, majd az eltávolított elektront elektrosztatikus potenciállal gyorsították. Ez a kifejezés ma már kerülendő.[4] Az ionizációs energiát befolyásoló néhány tényező:
- Az atommag töltése: minél nagyobb az atommag töltése, annál erősebben kötődnek az elektronok az atommaghoz, így az ionizációs energia értéke is nagyobb lesz.
- Az elektronhéjak száma: minél nagyobb méretű az atom, annál gyengébben kötődnek az elektronok az atommaghoz, az ionizációs energia ezért kisebb lesz.
- Effektív magtöltés (Zeff): minél nagyobb a törzselektronok penetrációja és – az atommag pozitív töltését – árnyékoló hatása, annál kevésbé kötődnek a maghoz a külső elektronok és annál kisebb lesz számukra Zeff, így ionizációs energiájuk is kisebb lesz.[5]
- Az ionizált atompálya típusa: a stabilabb elektronkonfigurációval rendelkező atom nehezebben ad le elektront, így ionizációs energiája nagyobb.
- Az alhéj betöltöttsége is számít: ha egy alhéj félig vagy teljesen be van töltve, akkor nehezebben lehet róla elektronokat eltávolítani.
Értékek és trendek
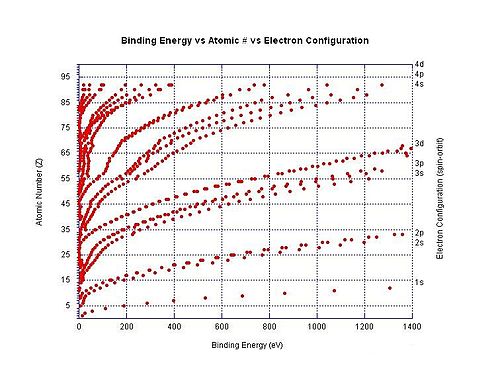
Az (n+1)-edik ionizációs energia általában magasabb, mint az n-edik. Ha a következő elektront ugyanarról a héjról kell eltávolítani, akkor az ionizációs energia növekedését elsősorban az okozza, hogy nagyobb pozitív töltésű ionból kell a negatív elektront kiszakítani: a nagyobb töltés miatt erősebb az elektrosztatikus vonzás, ennek leküzdése több energiát igényel. Ráadásul ha a következő elektron belsőbb pályán található, akkor a mag és elektron közötti jóval kisebb távolság nagyobb elektrosztatikus vonzóerővel jár, és ezt az erőt nagyobb úthosszon kell legyőzni ahhoz, hogy az elektront az atomból eltávolítsuk. Ez a két tényező tovább növeli az ionizációs energiát.
A harmadik periódus elemeire néhány érték az alábbi táblázatban látható:
| Elem | Első | Második | Harmadik | Negyedik | Ötödik | Hatodik | Hetedik |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4560 | |||||
| Mg | 738 | 1450 | 7730 | ||||
| Al | 577 | 1816 | 2881 | 11600 | |||
| Si | 786 | 1577 | 3228 | 4354 | 16100 | ||
| P | 1060 | 1890 | 2905 | 4950 | 6270 | 21200 | |
| S | 999,6 | 2295 | 3375 | 4565 | 6950 | 8490 | 27107 |
| Cl | 1256 | 2260 | 3850 | 5160 | 6560 | 9360 | 11000 |
| Ar | 1520 | 2665 | 3945 | 5770 | 7230 | 8780 | 12000 |
Az egymást követő moláris ionizációs energiákban nagy ugrás jelentkezik a nemesgázkonfiguráció átlépésekor. Például a fenti táblázatban látható, hogy a magnézium első két moláris ionizációs energiája (a magnéziumatom két 3s elektronjának eltávolítása) a harmadiknál sokkal kisebb, utóbbi ugyanis a neon konfigurációjú Mg2+-ból a 2p elektron eltávolítását igényli, ez azonban jóval közelebb van a maghoz, mint az előző 3s elektron.
Az ionizációs energia a periódusos rendszeren belül is trendet mutat. Egy perióduson belül balról jobbra, vagy egy csoporton belül felfelé haladva az első ionizációs energia néhány kivételtől – például a fenti táblázatban az alumínium és kén esetétől – eltekintve általában nő. Ahogy egy perióduson belül nő a mag töltése, úgy csökken az atom sugara, és kerül közelebb a maghoz az elektronfelhő.
Elektrosztatikus magyarázat
Az atomok ionizációs energiája megjósolható, ha megvizsgáljuk az elektrosztatikus potenciált a Bohr-féle atommodellben.
Tekintsünk egy −e töltésű elektront és egy +Ze töltésű atommagot, ahol Z a magban található protonok száma. A Bohr-modell szerint ha egy elektron megközelítene egy atomot és az megkötné, akkor annak magjától egy meghatározott a távolságba kerülne. Az atommagtól a távolságra a V elektrosztatikus potenciál egy végtelen távol lévő pontra vonatkoztatva az alábbi:
Mivel az elektron töltése negatív, a pozitív elektrosztatikus potenciál befelé húzza. Az ahhoz szükséges energia, hogy az elektron ki tudjon jutni ebből a potenciálgödörből és elhagyja az atomot:
Ezzel még nem tártuk fel teljesen a problémát, mivel az a távolság ismeretlen változó. További pontosítás tehető, ha a kémiai elemek minden egyes elektronjához hozzárendelünk egy jellemző távolságot, melyet úgy választunk meg, hogy a fenti képlet egyezzen a kísérleti eredményekkel.
Ezt a modellt jelentősen bővíthetjük félklasszikus megfontolásokkal, amikor is a momentum kvantált. Ez a megközelítés nagyon jól működik a hidrogénatom esetén, amelyben csak egyetlen elektron található. Körpálya esetén az impulzusmomentum nagysága:
Az atom teljes energiája a mozgási és a potenciális energia összege:
A mozgási energia tagból a sebesség kiejthető, ha a Coulomb-féle vonzást egyenlőnek vesszük a centripetális erővel:
Az impulzusmomentumot v-re megoldva és ezt behelyettesítve a kinetikus energia kifejezésébe az alábbi összefüggés adódik:
Ez megalapozza a sugár n-től való függését, azaz:
Az energiát így Z, e és r segítségével fejezhetjük ki. A fenti összenergiát leíró kifejezésbe behelyettesítve a kinetikus energia új értékét kapjuk:
A legkisebb érték akkor adódik, ha n=1, r pedig az a0 Bohr-sugár, melynek értéke . Az energia így kifejezhető a Bohr-sugár segítségével:
Kvantummechanikai leírás
A teljesebb kvantummechanikai kép szerint az elektron helyét legjobban egy elektronfelhőn, azaz atompályán belüli valószínűségi eloszlással lehet leírni. Az energia ezen atompálya egészének integrálásával kapható. A felhő matematikai leírása a hullámfüggvény, melyet Slater determinánsokból képeznek.
Az n-edik ionizációs energia kiszámításához általánosságban a és elektront tartalmazó rendszerek energiájának meghatározása szükséges. Ezen energiákat pontosan csak a legegyszerűbb rendszerek (azaz például a hidrogénatom) esetében lehet kiszámítani, aminek elsősorban az az oka, hogy az elektronkorrelációs kifejezések integrálása bonyolult. Emiatt a gyakorlatban közelítő módszereket használnak, ezek bonyolultsága (számítási ideje) és pontossága – a kísérleti adatokkal való egyezése – változó. A legegyszerűbb közelítésben az ionizációs energiák a Koopmans-tétel alapján számíthatók.
A molekulák vertikális és adiabatikus ionizációs energiája

A molekulák ionizációja gyakran azok alakjának változását okozza, és kétféle (első) ionizációs energia definiálható – adiabatikus és vertikális.[6]
Adiabatikus ionizációs energia
Egy molekula adiabatikus ionizációs energiája az a legkisebb energiamennyiség, mely ahhoz szükséges, hogy egy semleges molekulából eltávolítsunk egy elektront, azaz a semleges részecske és a pozitív ion rezgési alapállapotának (v" = 0, illetve v' = 0 szint) energiakülönbsége. Az egyes részecskék meghatározott egyensúlyi geometriája nem befolyásolja ennek értékét.
Vertikális ionizációs energia
Mivel az ionizáció során a molekula geometriája változhat, egyéb átmenet is létezhet a semleges részecske rezgési alapállapota és a pozitív ion gerjesztett rezgési állapotai között. Más szóval az ionizációhoz a rezgés gerjesztése társul. Az ilyen átmenetek intenzitását a Franck–Condon-elv magyarázza, amely szerint a legvalószínűbb és legnagyobb intenzitású átmenet az ion azon gerjesztett rezgési állapotánk felel meg, amelynek geometriája a semleges molekuláéval azonos. Ezt az átmenetet nevezik „vertikális” ionizációnak, mivel a potenciálisenergia-diagramon ez egy teljesen függőleges vonalnak felel meg (lásd 1. ábra).
Kétatomos molekula esetében a geometriát a két atom közötti kémiai kötés hossza határozza meg. Ha egy elektront eltávolítunk egy kötő molekulapályáról, akkor a kötés erőssége gyengül, a hossza pedig nő. Az 1. ábrán az alsó potenciálgörbe a semleges molekuláé, a felső a pozitív ioné. Mindkét görbe a kötéshossz függvényében ábrázolja a potenciális energiát. A vízszintes vonalak az egyes – rezgési hullámfüggvénnyel társuló – rezgési szinteknek felelnek meg. Mivel az ionban a kötés gyengébb, benne a kötéshossz nagyobb. Ezt a hatást mutatja, hogy az ionban a potenciális energia minimuma a semleges részecskééhez képest jobbra – a nagyobb távolság felé – van eltolódva. Az adiabatikus ionizáció az ion rezgési alapállapotába irányuló átlós átmenet. A vertikális ionizáció az ion rezgési gerjesztésével is járhat, ami többletenergiát igényel.
Számos esetben az adiabatikus ionizációs energia az érdekesebb fizikai mennyiség, mivel a két potenciálisenergia-felület közötti energiakülönbséget adja meg. Ugyanakkor az adiabatikus ionizációs energiát kísérletileg általában nehéz meghatározni, míg a vertikális átmenet energiáját könnyű azonosítani és mérni.
Az ionizációs energiához hasonló mennyiségek más rendszerekben
Bár az ionizációs energia kifejezést nagyrészt gázfázisú atomokra vagy molekulákra használjuk, több hasonló – valamilyen fizikai rendszerből egy elektron eltávolításához szükséges – mennyiség is létezik.
Az elektron kötési energiája
Az elektron kötési energiája az ionizációs energia általánosítása, bármekkora töltésű részecskére értelmezhető. A kloridionban az elektron kötési energiája például az a legkisebb energia, amely ahhoz szükséges, hogy egy −1 töltésű klóratomból egy elektront eltávolítsunk. Ebben a példában az elektron kötési energiája megegyezik a semleges klóratom elektronaffinitásának értékével. További példának tekintsük a dikarboxilát aniont – −O2C(CH2)8CO−2 –, ennél az elektron kötési energiája az anionból egy elektron eltávolításához szükséges energia.
Kilépési munka
A kilépési munka az a legkisebb energiamennyiség, amely egy elektronnak egy szilárd felületből történő eltávolításához szükséges.
Jegyzetek
- ↑ Inorganic Chemistry, 2nd, Prentice Hall, 41. o. (1999. január 10.). ISBN 0-13-841891-8
- ↑ Ionization Energy. ChemWiki. University of California, Davis, 2013. október 2.
- ↑ Advanced Inorganic Chemistry, 5th, John Wiley, 1381. o. (1988. január 10.). ISBN 0-471-84997-9
- ↑ ionization potential. IUPAC gold book
- ↑ Lang, Peter F. (2003). „Ionization Energies of Atoms and Atomic Ions” (angol nyelven). Journal of Chemical Education 80 (8), 938. o. DOI:10.1021/ed080p938.
- ↑ The difference between a vertical ionization energy and adiabatic ionization energy. Computational Chemistry Comparison and Benchmark Database. National Institute of Standards and Technology
Fordítás
Ez a szócikk részben vagy egészben az Ionization energy című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.











