Geometria epipolare

La geometria epipolare è la geometria della visione stereoscopica. Essa descrive le relazioni e i vincoli geometrici che legano due immagini 2D della stessa scena 3D catturata da due fotocamere con posizione e orientamento distinto.
Geometria Epipolare
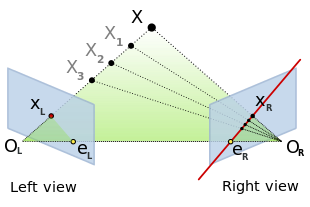
Immaginiamo di voler fotografare un elemento nello spazio 3D nel punto X tramite due fotocamere centrate in OL e OR. Il punto in questione verrà rispettivamente proiettato sul piano immagine della fotocamera sinistra in xL e in xR nel piano immagine della fotocamera destra.
La proiezione del punto X sul piano immagine delle rispettive fotocamere avviene tramite una trasformazione proiettiva PL (e PR) ovvero una matrice che tiene conto della posizione, dell'orientamento e dei parametri formali della rispettiva fotocamera. La relazione può essere espressa matematicamente come
Punti epipolari
Poiché i centri OL e OR di ogni camera sono in posizioni distinte è possibile proiettare l'uno sul piano immagine dell'altro.
I due punti eL e eR prendono il nome di epipoli o punti epipolari.
Rette epipolari
Il punto xL può essere visto come l'intersezione della retta passante per OL e X, chiamata raggio di proiezione, con il piano immagine della fotocamera sinistra.
Immaginiamo quindi di proiettare tale retta sul piano immagine destro. Poiché la trasformazione proiettiva è un omografia se il raggio di proiezione collega X con OL allora la sua proiezione collegherà le proiezioni dei due punti. Ovvero sarà la retta passante per xR e la proiezione di OL, ovvero proprio il punto epipolare destro eR. Esprimendo i due punti in coordinate omogenee la retta può essere espressa come
Tale retta prende il nome di retta epipolare. Lo stesso ragionamento può essere fatto analogamente con i raggi di proiezione della camera destra.
Piano epipolare
Come interpretazione alternativa consideriamo il piano su cui giacciono i punti X, OL e OR. Questo piano prende il nome di piano epipolare. Il piano epipolare associato ad un punto X intercetta i piani immagine esattamente nelle rette epipolari associate a X. Tutti i piani epipolari si incontrano nella retta che unisce i due epipoli che prende il nome di linea di base.
Ricostruzione della scena
La geometria epipolare ricopre un ruolo fondamentale nella ricostruzione di una scena tridimensionale a partire da una coppia di immagini stereoscopiche. La ricostruzione avviene tramite i seguenti passi:
- Data una lista di punti corrispondenti nelle due immagini viene calcolata la matrice fondamentale F ovvero una matrice 3x3 di rango due tale che .
- Dalla matrice fondamentale vengono ricavate le matrici che rappresentano le trasformazioni proiettive delle due camere tramite le relazioni:
. - Per ogni coppia di punti corrispondenti nell'immagine si stima il punto X tramite le informazioni ricavate dalle due matrici di proiezione.
Bibliografia
- (EN) Richard Hartley, Andrew Zisserman, Multiple View Geometry in Computer Vision, 2ª ed., Cambridge University Press, 2004, ISBN 978-0-521-54051-3.
Altri progetti
 Wikimedia Commons contiene immagini o altri file su Geometria epipolare
Wikimedia Commons contiene immagini o altri file su Geometria epipolare
| Controllo di autorità | GND (DE) 7759349-2 |
|---|






![{\displaystyle P_{L}=[I|0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dc229802b0c8129e634198e111c88f507ab1c10)
![{\displaystyle P_{R}=[[e_{R}]\times F|e_{R}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a52d3e28a0aef270ebc900fe62f679b3c5910a1d)