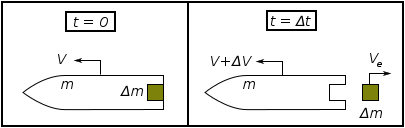ツィオルコフスキーの公式

ツィオルコフスキーの公式（ツィオルコフスキーのこうしき）は、1897年にコンスタンチン・ツィオルコフスキーによって示されたロケット推進に関する公式である。

ロケットの初期の質量を $m 0$ 、時間 $T$ 経過後の質量を $m T$ 、質量変化は推進剤として速度 $w$ で噴射されたものとすると、時間 $T$ 経過後のロケットの速度変化分 $Δ V$ は次の式で表される（ $ln$ は自然対数）。

\Delta V=w\ln {\frac {m_{0}{m_{T

導出

質量が $m$ 、推進剤の噴射速度が $w$ （上図では $V e$ ）であるロケットを考える。微少な時間 $Δ t$ の間に噴射する推進剤の質量を $Δ m$ 、その推進剤の噴射による増速度を $Δ v$ とすると、以下のように運動量保存則が成り立つ。

$(m+\Delta m)v=m(v+\Delta v)+\Delta m(v-w)$

これを展開して整理すると、次式のような関係が成り立つ。

m\Delta v=w\Delta m

これを微分方程式とみて、増速度の合計（積分）をとるために式を変形すると、

\int \mathrm {d} v=-w\int {\frac {1}{m}\mathrm {d} m

これを、ロケットの初速度を $0$ 、初期の質量を $m 0$ 、時間 $T$ 経過後の質量を $m T$ として解くと、

v=w\ln {\frac {m_{0}{m_{T

となり、時間 $T$ 経過後のロケットの速度 $v$ が導出できる。

上記式の $m 0 / m T$ を質量比と呼ぶ。式から判るとおり、噴射速度と質量比が高いほど、最終的な到達速度も高くなる。それは逆に、到達速度を高くするには、噴射速度か質量比を上げなければならないことを意味する。

また、ロケットの性能を示すのによく使われる噴射速度を重力加速度で割った値とみることのできる値比推力 $I sp$ を導入すると、重力加速度 $g$ も使って、

v=I_{\mathrm {sp} }g\ln {\frac {m_{0}{m_{T

となる。

例1 打ち上げ時の総質量

LE-7Aエンジン（液体酸素・液体水素を推進剤とし、比推力 440 s）を使用した 60 t のSSTOを、衛星軌道に到達させるために第一宇宙速度 7.9 km/s まで加速したい場合、推進剤も含めた打ち上げ時の総質量は、

m_{0}=m_{T}\exp \left({\frac {\Delta V}{I_{sp}\,g}\right)=374.8~\mathrm {t}

から 375 t となり、自重を引くことで最低でも 315 t の推進剤が必要なことがわかる（この自重の中には、膨大な量の推進剤を入れておく燃料タンクやエンジン、軌道へ運ぶペイロードその他の構造物の質量を含む）。質量比は6.25となる。この条件で、地球の大気や自転の影響を無視して加速を水平方向にした場合、地表面をすれすれに回る衛星として存在できる。

なお、上記はツィオルコフスキーの公式だけの話であり、実際の地表からの打ち上げでは大気の影響を避けるため、まず垂直方向に打ち上げる。この場合、自重以上の推力（LE-7Aエンジン1機の推力は 100 tf 程度）が無ければ、重力のために 1 mm たりとも昇がらない（専門用語では重力による損をまとめて重力損失と言う）し、空気抵抗、推力損失（大気圧中でロケットエンジンを使用することによる損失）もある（実際の離床にはSSTOにLE-7Aを複数付けることや固体ロケットブースターが必須である）。また、SSTOに翼を付け揚力を得て水平に加速すれば、自重以上の推力は必ずしも必要はないが、空気抵抗や推力損失がより大きくなる。宇宙速度に達するための推進剤のほかに、その高度に達するまでの推進剤が必要となる。

例2 多段式ロケット

例1と同じく、LE-7Aエンジン（比推力 440 s）を用いたロケットを考える。打ち上げ時質量 100 t、ペイロード含む構造質量 20 t（質量比5）の1段式ロケットの速度増分は、

\Delta V=I_{\mathrm {sp} }\,g\,\ln {\frac {m_{0}{m_{T}=6.94~\mathrm {km~s^{-1}

となり、約 6.9 km/s の速度を得る。

次に、第1段、第2段ともに打ち上げ時質量 50 t、ペイロード含む構造質量 10 t（各段の質量比5は上の1段式ロケットと変わらない）で、ロケット全体の打ち上げ時質量が 100 t である2段式ロケットを考える。ツィオルコフスキーの公式の導出と同じ考え方でこの2段式ロケットの速度増分を求めると、

\Delta V=I_{\mathrm {sp1} }\,g\,\ln {\frac {m_{01}{m_{T1}+I_{\mathrm {sp2} }\,g\,\ln {\frac {m_{02}{m_{T2}=9.14~\mathrm {km~s^{-1}

となり、約 9.1 km/s という、1段式ロケットと同じ質量比のロケットでありながらも1段式ロケットよりもはるかに大きな速度を得る。この利点のため、2018年現在すべての衛星打ち上げ機は多段式ロケットである。

補足

「全てのロケットはこの式に従う」という説明を見掛けることもあるが、前述の例にもあるように、重力の影響（いわゆる「重力損失」）や空気による抗力（空気抵抗）といったものは含んでいないので、たとえば、実際の打ち上げでは特に重要な第1段のエンジンをこの公式だけで評価するのは誤りである。

参考文献

松浦晋也『われらの有人宇宙船-日本独自の宇宙輸送システム「ふじ」-』裳華房、2003年。ISBN 4-7853-8758-0。 ^{[要ページ番号]}

ツィオルコフスキーの公式

導出

例1 打ち上げ時の総質量

例2 多段式ロケット

補足

参考文献

関連項目