三相交流の波形 三相交流 (さんそうこうりゅう、英語 : three-phase electric power )とは、起電力(電圧)の位相を120度(
2
π
/
3
{\displaystyle 2\pi /3}
[ 1] 電力系統 において主流の送電方法である[ 2] 電動機 [ 3] AEG が最も寄与した[ 2]
三相交流による送電(三相三線式 )は同条件で比較した場合、単相交流 (単相二線式 )よりも導体の使用量が少なくて済むため経済的である[ 3] [ 4] ガリレオ・フェラリス 、ミハイル・ドリヴォ=ドブロヴォルスキー 、Jonas Wenström とニコラ・テスラ 達の働きによって1880年代末に発明された[ 2]
三相交流のうち、起電力(電圧)の大きさが等しく、位相が120度ずつずれているものを特に対称三相交流 という。式で表すと次の通り[ 5]
E
a
˙
=
E
∠
0
=
E
e
j
0
=
E
E
b
˙
=
E
∠
−
2
π
3
=
E
e
−
j
2
π
/
3
E
c
˙
=
E
∠
−
4
π
3
=
E
e
−
j
4
π
/
3
{\displaystyle {\begin{aligned}{\dot {E_{a}&=E\angle 0=Ee^{j0}=E\\{\dot {E_{b}&=E\angle -{\frac {2\pi }{3}=Ee^{-j2\pi /3}\\{\dot {E_{c}&=E\angle -{\frac {4\pi }{3}=Ee^{-j4\pi /3}\\\end{aligned}
三相交流電圧のベクトル図 瞬時値形式で書いた場合は次の通り[ 6]
e
a
(
t
)
=
E
sin
(
ω
t
)
e
b
(
t
)
=
E
sin
(
ω
t
−
2
3
π
)
e
c
(
t
)
=
E
sin
(
ω
t
−
4
3
π
)
{\displaystyle {\begin{aligned}e_{a}(t)&=E\sin(\omega t)\\e_{b}(t)&=E\sin(\omega t-{\frac {2}{3}\pi )\\e_{c}(t)&=E\sin(\omega t-{\frac {4}{3}\pi )\\\end{aligned}
[ 7] [ 8]
E
a
˙
+
E
b
˙
+
E
c
˙
=
0
e
a
(
t
)
+
e
b
(
t
)
+
e
c
(
t
)
=
0
{\displaystyle {\begin{aligned}{\dot {E_{a}+{\dot {E_{b}+{\dot {E_{c}&=0\\e_{a}(t)+e_{b}(t)+e_{c}(t)&=0\\\end{aligned}
瞬時値形式とベクトル形式は、形が違うだけで同じものを指し示している。そのためどちらか一方の形式において、証明すれば十分なのだが、ここではそれぞれの形式における証明方法を記載している。
三角関数の加法定理 を用いる。
e
a
(
t
)
+
e
b
(
t
)
+
e
c
(
t
)
=
E
{
sin
ω
t
+
sin
(
ω
t
−
2
3
π
)
+
sin
(
ω
t
−
4
3
π
)
}
=
E
(
sin
ω
t
−
1
2
sin
ω
t
−
3
2
cos
ω
t
−
1
2
sin
ω
t
+
3
2
cos
ω
t
)
=
0
{\displaystyle {\begin{aligned}e_{a}(t)+e_{b}(t)+e_{c}(t)&=E\left\{\sin \omega t+\sin \left(\omega t-{\frac {2}{3}\pi \right)+\sin \left(\omega t-{\frac {4}{3}\pi \right)\right\}\\&=E\left(\sin \omega t-{\frac {1}{2}\sin \omega t-{\frac {\sqrt {3}{2}\cos \omega t-{\frac {1}{2}\sin \omega t+{\frac {\sqrt {3}{2}\cos \omega t\right)\\&=0\end{aligned}
以上の計算により、三つの起電力の和が0になることが示された[ 7]
オイラーの公式 を用いる。
E
a
˙
+
E
b
˙
+
E
c
˙
=
E
e
j
0
+
E
e
−
j
2
π
/
3
+
E
e
−
j
4
π
/
3
=
E
e
j
θ
(
1
+
e
−
j
2
π
/
3
+
e
−
j
4
π
/
3
)
=
E
e
j
θ
(
1
+
cos
2
3
π
−
j
sin
2
3
π
+
cos
4
3
π
−
j
sin
4
3
π
)
=
E
e
j
θ
(
1
−
1
2
−
j
3
2
−
1
2
+
j
3
2
)
=
0
{\displaystyle {\begin{aligned}{\dot {E_{a}+{\dot {E_{b}+{\dot {E_{c}&=Ee^{j0}+Ee^{-j2\pi /3}+Ee^{-j4\pi /3}\\&=Ee^{j\theta }\left(1+e^{-j2\pi /3}+e^{-j4\pi /3}\right)\\&=Ee^{j\theta }\left(1+\cos {\frac {2}{3}\pi -j\sin {\frac {2}{3}\pi +\cos {\frac {4}{3}\pi -j\sin {\frac {4}{3}\pi \right)\\&=Ee^{j\theta }\left(1-{\frac {1}{2}-j{\frac {\sqrt {3}{2}-{\frac {1}{2}+j{\frac {\sqrt {3}{2}\right)\\&=0\\\end{aligned}
以上の計算により、三つの起電力の和が0になることが示された[ 8]
対称三相交流であり、各起電力に接続されている負荷インピーダンスがたがいに等しい(平衡負荷 )場合を考える。
このとき各負荷に流れる電流は
I
a
˙
=
I
∠
−
θ
=
I
e
−
j
θ
I
b
˙
=
I
∠
−
(
θ
+
2
π
3
)
=
I
e
−
j
(
θ
+
2
π
/
3
)
I
c
˙
=
I
∠
−
(
θ
+
4
π
3
)
=
I
e
−
j
(
θ
+
4
π
/
3
)
{\displaystyle {\begin{aligned}{\dot {I_{a}&=I\angle -\theta =Ie^{-j\theta }\\{\dot {I_{b}&=I\angle -\left(\theta +{\frac {2\pi }{3}\right)=Ie^{-j(\theta +2\pi /3)}\\{\dot {I_{c}&=I\angle -\left(\theta +{\frac {4\pi }{3}\right)=Ie^{-j(\theta +4\pi /3)}\\\end{aligned}
となる。(
θ
{\displaystyle \theta }
三相平衡交流 という[ 5]
三相交流電流のベクトル図 瞬時値形式で書いた場合は次の通り。
i
a
(
t
)
=
I
sin
(
ω
t
−
θ
)
i
b
(
t
)
=
I
sin
(
ω
t
−
θ
−
2
3
π
)
i
c
(
t
)
=
I
sin
(
ω
t
−
θ
−
4
3
π
)
{\displaystyle {\begin{aligned}i_{a}(t)&=I\sin(\omega t-\theta )\\i_{b}(t)&=I\sin(\omega t-\theta -{\frac {2}{3}\pi )\\i_{c}(t)&=I\sin(\omega t-\theta -{\frac {4}{3}\pi )\\\end{aligned}
平衡三相交流であれば、三つの電流の和は0になる[ 9]
I
a
˙
+
I
b
˙
+
I
c
˙
=
0
i
a
(
t
)
+
i
b
(
t
)
+
i
c
(
t
)
=
0
{\displaystyle {\begin{aligned}{\dot {I_{a}+{\dot {I_{b}+{\dot {I_{c}&=0\\i_{a}(t)+i_{b}(t)+i_{c}(t)&=0\\\end{aligned}
電圧・電流の大きさが一定でない、もしくは位相差が120°でない交流のことを三相不平衡交流 という。各負荷のインピーダンスが等しくなかったり、短絡 ・地絡 などの故障が起きたりした場合に三相不平衡交流となる。なおその回路のことを三相不平衡回路 という[ 10]
三相不平衡回路の回路計算は複雑であるため、2つの対称三相交流と1つの単相交流に変換し対称交流回路と単相回路として扱う対称座標法(英語版 、ドイツ語版 、スペイン語版 、フランス語版 ) と呼ばれる計算方法が用いられる[ 10]
三相交流によって電源と負荷を接続する場合、例えば図のように接続する。
これらの接続方式を順に、Y-Δ接続・Y-Y接続・Δ-Y接続・Δ-Δ接続 と呼ぶ[ 11]
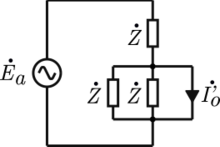
中性線ありのY-Y接続 中性線を取り除いたY-Y接続 図のように電源と負荷を接続した場合を考える。(この接続方式をY-Y接続 [ 12] 平衡負荷 )[ 5]
このとき中性線に流れる電流は0 になり、中性点間の導線を取り除くことができる[ 12]
上記回路(中性点を省略していない方)に重ねの理 を適用する。電源が
E
a
˙
{\displaystyle {\dot {E_{a}
I
o
˙
{\displaystyle {\dot {I_{o}
I
o
˙
′
{\displaystyle {\dot {I_{o}^{\prime }
E
b
˙
{\displaystyle {\dot {E_{b}
I
o
˙
′
′
{\displaystyle {\dot {I_{o}^{\prime \prime }
E
c
˙
{\displaystyle {\dot {E_{c}
I
o
˙
′
′
′
{\displaystyle {\dot {I_{o}^{\prime \prime \prime }
電源Eaのみの回路図(重ねの理) 電源Ebのみの回路図(重ねの理) 電源Ecのみの回路図(重ねの理) すると次のような回路となるから、負荷インピーダンスを
Z
˙
{\displaystyle {\dot {Z}
I
o
˙
′
=
E
a
˙
Z
˙
I
o
˙
′
′
=
E
b
˙
Z
˙
I
o
˙
′
′
′
=
E
c
˙
Z
˙
{\displaystyle {\begin{aligned}{\dot {I_{o}^{\prime }&={\frac {\dot {E_{a}{\dot {Z}\\{\dot {I_{o}^{\prime \prime }&={\frac {\dot {E_{b}{\dot {Z}\\{\dot {I_{o}^{\prime \prime \prime }&={\frac {\dot {E_{c}{\dot {Z}\\\end{aligned}
と求めることができる。重ねの理より
I
o
˙
{\displaystyle {\dot {I_{o}
I
o
˙
=
I
o
˙
′
+
I
o
˙
′
′
+
I
o
˙
′
′
′
=
1
Z
˙
(
E
a
˙
+
E
b
˙
+
E
c
˙
)
{\displaystyle {\begin{aligned}{\dot {I_{o}&={\dot {I_{o}^{\prime }+{\dot {I_{o}^{\prime \prime }+{\dot {I_{o}^{\prime \prime \prime }\\&={\frac {1}{\dot {Z}({\dot {E_{a}+{\dot {E_{b}+{\dot {E_{c})\\\end{aligned}
となる。ここで対称三相交流の性質 で解説したように
E
a
˙
+
E
b
˙
+
E
c
˙
=
0
{\displaystyle {\dot {E_{a}+{\dot {E_{b}+{\dot {E_{c}=0}
I
o
˙
=
0
{\displaystyle {\dot {I_{o}=0}
が成り立ち、中性点間の導線を取り除いても構わないことが分かる[ 8]
三相平衡回路の、伝送電力の瞬時値
p
(
t
)
{\displaystyle p(t)}
p
(
t
)
=
3
2
V
I
cos
θ
{\displaystyle p(t)={\frac {3}{2}VI\cos {\theta }
となる[ 13]
V
{\displaystyle V}
I
{\displaystyle I}
cos
θ
{\displaystyle \cos {\theta }
三相平衡回路の起電力の瞬時値・三相平衡回路に流れる電流の瞬時値は、次のように書ける。(
θ
{\displaystyle \theta }
{
v
a
(
t
)
=
V
sin
(
ω
t
)
v
b
(
t
)
=
V
sin
(
ω
t
−
2
3
π
)
v
c
(
t
)
=
V
sin
(
ω
t
−
4
3
π
)
{\displaystyle \left\{\begin{aligned}v_{a}(t)&=V\sin(\omega t)\\v_{b}(t)&=V\sin(\omega t-{\frac {2}{3}\pi )\\v_{c}(t)&=V\sin(\omega t-{\frac {4}{3}\pi )\\\end{aligned}\right.}
{
i
a
(
t
)
=
I
sin
(
ω
t
+
θ
)
i
b
(
t
)
=
I
sin
(
ω
t
+
θ
−
2
3
π
)
i
c
(
t
)
=
I
sin
(
ω
t
+
θ
−
4
3
π
)
{\displaystyle \left\{\begin{aligned}i_{a}(t)&=I\sin(\omega t+\theta )\\i_{b}(t)&=I\sin(\omega t+\theta -{\frac {2}{3}\pi )\\i_{c}(t)&=I\sin(\omega t+\theta -{\frac {4}{3}\pi )\\\end{aligned}\right.}
これらの式を
p
(
t
)
{\displaystyle p(t)}
p
(
t
)
=
v
a
(
t
)
i
a
(
t
)
+
v
b
(
t
)
i
b
(
t
)
+
v
c
(
t
)
i
c
(
t
)
{\displaystyle p(t)=v_{a}(t)i_{a}(t)+v_{b}(t)i_{b}(t)+v_{c}(t)i_{c}(t)}
に代入して計算を進める[ 13] 三角関数の積和公式 を用いている。
p
(
t
)
=
v
a
(
t
)
i
a
(
t
)
+
v
b
(
t
)
i
b
(
t
)
+
v
c
(
t
)
i
c
(
t
)
=
V
I
{
sin
(
ω
t
)
sin
(
ω
t
+
θ
)
+
sin
(
ω
t
−
2
π
3
)
sin
(
ω
t
+
θ
−
2
π
3
)
+
sin
(
ω
t
−
4
π
3
)
sin
(
ω
t
+
θ
−
4
π
3
)
}
=
1
2
V
{
cos
(
−
θ
)
−
cos
(
2
ω
t
+
θ
)
+
cos
(
−
θ
)
−
cos
(
2
ω
t
+
θ
−
4
π
3
)
+
c
o
s
(
−
θ
)
−
cos
(
2
ω
t
+
θ
−
8
π
3
)
}
=
3
2
V
I
cos
θ
+
1
2
V
{
I
sin
(
ω
′
t
+
θ
′
)
+
I
sin
(
ω
′
t
+
θ
′
−
2
3
π
)
+
I
sin
(
ω
′
t
+
θ
′
−
4
3
π
)
}
{\displaystyle {\begin{aligned}p(t)&=v_{a}(t)i_{a}(t)+v_{b}(t)i_{b}(t)+v_{c}(t)i_{c}(t)\\&=VI\left\{\sin(\omega t)\sin(\omega t+\theta )+\sin(\omega t-{\frac {2\pi }{3})\sin(\omega t+\theta -{\frac {2\pi }{3})+\sin(\omega t-{\frac {4\pi }{3})\sin(\omega t+\theta -{\frac {4\pi }{3})\right\}\\&={\frac {1}{2}V\left\{\cos(-\theta )-\cos(2\omega t+\theta )+\cos(-\theta )-\cos(2\omega t+\theta -{\frac {4\pi }{3})+cos(-\theta )-\cos(2\omega t+\theta -{\frac {8\pi }{3})\right\}\\&={\frac {3}{2}VI\cos \theta +{\frac {1}{2}V\left\{I\sin(\omega ^{\prime }t+\theta ^{\prime })+I\sin(\omega ^{\prime }t+\theta ^{\prime }-{\frac {2}{3}\pi )+I\sin(\omega ^{\prime }t+\theta ^{\prime }-{\frac {4}{3}\pi )\right\}\end{aligned}
ω
′
=
2
ω
,
θ
′
=
θ
−
π
/
2
{\displaystyle \omega ^{\prime }=2\omega ,\theta ^{\prime }=\theta -\pi /2}
p
(
t
)
{\displaystyle p(t)}
p
(
t
)
=
3
2
V
I
cos
θ
{\displaystyle p(t)={\frac {3}{2}VI\cos {\theta }
となる。
電源の接続方法には、Y結線 ・Δ結線 ・V結線 の三つがある[ 11] [ 14] Y結線 ・Δ結線 が存在する。
負荷結線の、相電流・相電圧・線電流・線間電圧の定義は、電源と同じである[ 11]
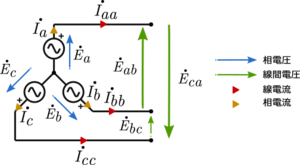
三相交流におけるY結線図 Y結線 (ワイけっせん, ほしがたけっせん, スターけっせん)は、三相各相をその一端の中性点で接続する結線[ 15] 星形結線 (ほしがたけっせん)、スター結線 とも表記する[ 16]
各相間の電位差を線間電圧 (せんかんでんあつ)といい、各相と大地間の電位差を相電圧 (そうでんあつ)という。また、結線外の各相の電流を線電流 (せんでんりゅう)といい、結線内の各相の電流を相電流 (そうでんりゅう)という。
Y結線における、線間電圧と相電圧の関係は次の通り。
線間電圧の大きさ は、相電圧の大きさ の
3
{\displaystyle {\sqrt {3}
線間電圧の位相は、線間電圧の正極性につながっている相電圧よりも30°進んでいる
線間電流は線電流に等しい 上の三つの関係を数式で表すと
E
˙
a
b
=
3
E
a
˙
∠
π
6
E
˙
b
c
=
3
E
b
˙
∠
π
6
E
˙
c
a
=
3
E
c
˙
∠
π
6
I
˙
a
a
=
I
˙
a
I
˙
b
b
=
I
˙
b
I
˙
c
c
=
I
˙
c
{\displaystyle {\begin{aligned}{\dot {E}_{ab}&={\sqrt {3}{\dot {E_{a}\angle {\frac {\pi }{6}\\{\dot {E}_{bc}&={\sqrt {3}{\dot {E_{b}\angle {\frac {\pi }{6}\\{\dot {E}_{ca}&={\sqrt {3}{\dot {E_{c}\angle {\frac {\pi }{6}\\{\dot {I}_{aa}&={\dot {I}_{a}\\{\dot {I}_{bb}&={\dot {I}_{b}\\{\dot {I}_{cc}&={\dot {I}_{c}\\\end{aligned}
となる[ 17]
三相交流におけるΔ結線図 Δ結線 (デルタけっせん, さんかくけっせん)は、三相各相を相電圧が加わる向きに接続し閉回路とする結線。三角結線 (さんかくけっせん)、デルタ結線 とも表記する[ 16]
Δ結線における、線電流と相電流の関係は次の通り。
線電流の大きさ は、相電流の大きさ の
3
{\displaystyle {\sqrt {3}
線電流の位相は、対応する相電流[ 注釈 1]
線間電圧は相電圧に等しい 上の三つの関係を数式で表すと
I
a
˙
=
3
I
˙
a
b
∠
−
π
6
I
b
˙
=
3
I
˙
b
c
∠
−
π
6
I
c
˙
=
3
I
˙
c
a
∠
−
π
6
E
˙
a
b
=
E
˙
a
E
˙
b
c
=
E
˙
b
E
˙
c
a
=
E
˙
c
{\displaystyle {\begin{aligned}{\dot {I_{a}&={\sqrt {3}{\dot {I}_{ab}\angle -{\frac {\pi }{6}\\{\dot {I_{b}&={\sqrt {3}{\dot {I}_{bc}\angle -{\frac {\pi }{6}\\{\dot {I_{c}&={\sqrt {3}{\dot {I}_{ca}\angle -{\frac {\pi }{6}\\{\dot {E}_{ab}&={\dot {E}_{a}\\{\dot {E}_{bc}&={\dot {E}_{b}\\{\dot {E}_{ca}&={\dot {E}_{c}\\\end{aligned}
となる[ 18]
Y結線とΔ結線の相電圧と相電流の差を利用し、かご形三相誘導電動機 をY結線で始動し、途中でΔ結線に切り替えることによって始動電流を3分の1に抑えるスターデルタ始動法 (Y-Δ始動法)[ 19]
三相交流におけるV結線図 V結線 (ブイけっせん)は、Δ結線より三相のうち一相を除いた結線である。
取り除かれた電源の端子間には、Δ結線のときと同じ電圧が発生する[ 20]
ただし有効電力の値はΔ結線の
1
/
3
{\displaystyle 1/{\sqrt {3}
3
{\displaystyle {\sqrt {3}
[ 21]
V結線の回路図より
V
c
˙
=
−
(
E
a
˙
+
E
b
˙
)
{\displaystyle {\dot {V_{c}=-({\dot {E_{a}+{\dot {E_{b})}
である。またΔ結線の回路図より
E
a
˙
+
E
b
˙
+
E
c
˙
=
0
E
c
˙
=
−
(
E
a
˙
+
E
b
˙
)
{\displaystyle {\begin{aligned}{\dot {E_{a}+{\dot {E_{b}+{\dot {E_{c}&=0\\{\dot {E_{c}&=-({\dot {E_{a}+{\dot {E_{b})\\\end{aligned}
となる。
V
c
˙
,
E
c
˙
{\displaystyle {\dot {V_{c},{\dot {E_{c}
V
c
˙
=
E
c
˙
{\displaystyle {\dot {V_{c}={\dot {E_{c}
[ 20]
V結線における線電流と相電流、線間電圧と相電圧の関係は次の通り。
線間電流の大きさ は線電流の大きさ に等しい(位相は異なる場合がある)
線間電圧の位相と大きさは、相電圧の位相と大きさに等しい 上の関係を数式で表すと次の通り[ 22]
I
˙
a
b
=
I
˙
a
I
˙
b
c
=
−
I
˙
c
I
˙
b
c
−
I
˙
a
b
=
I
˙
b
E
˙
a
b
=
E
˙
a
E
˙
b
c
=
E
˙
b
E
˙
c
a
=
V
˙
c
=
−
(
E
a
˙
+
E
b
˙
)
{\displaystyle {\begin{aligned}{\dot {I}_{ab}&={\dot {I}_{a}\\{\dot {I}_{bc}&=-{\dot {I}_{c}\\{\dot {I}_{bc}-{\dot {I}_{ab}&={\dot {I}_{b}\\{\dot {E}_{ab}&={\dot {E}_{a}\\{\dot {E}_{bc}&={\dot {E}_{b}\\{\dot {E}_{ca}&={\dot {V}_{c}=-({\dot {E_{a}+{\dot {E_{b})\\\end{aligned}
Y結線・Δ結線における有効電力
P
{\displaystyle P}
V
l
{\displaystyle V_{l}
I
l
{\displaystyle I_{l}
cos
θ
{\displaystyle \cos \theta }
P
=
3
V
l
I
l
cos
θ
{\displaystyle P={\sqrt {3}\ V_{l}I_{l}\cos \theta }
で表される[ 23]
P
v
{\displaystyle P_{v}
P
v
=
V
l
I
l
cos
θ
{\displaystyle P_{v}=\ V_{l}I_{l}\cos \theta }
となる[ 9]
Y結線・Δ結線における皮相電力
S
{\displaystyle S}
S
˙
{\displaystyle {\dot {S}
無効電力
Q
{\displaystyle Q}
S
=
3
V
l
I
l
S
˙
=
3
V
l
I
l
e
j
θ
Q
=
3
V
l
I
l
sin
θ
{\displaystyle {\begin{aligned}S&={\sqrt {3}\ V_{l}I_{l}\\{\dot {S}&={\sqrt {3}\ V_{l}I_{l}e^{j\theta }\\Q&={\sqrt {3}\ V_{l}I_{l}\sin \theta \\\end{aligned}
である[ 24]
三相交流による送電は、単相交流によるものと比較し以下のような利点がある。
電線一本あたりの送電電力が大きい。
同じ送電電力ならば、電線の質量を低減できる[ 25]
三相交流から単相交流を取り出すことができる。
三相交流からは回転磁界 を容易に得られる。(かご形三相誘導電動機 ) 3、4が正しいことは明らかである。しかし1、2が本当に正しいかどうかは、すぐにはわからない。ここでは1、2となる理由について解説する。
下の表は電線1線あたりの送電電力を比較したものである[ 注釈 2] [ 注釈 3] [ 注釈 4]
送電方式
送電電力[W]
1線あたりの送電電力[W]
送電電力比率[%]
単相二線式
E
I
cos
θ
{\displaystyle EI\cos \theta }
E
I
2
cos
θ
{\displaystyle {\frac {EI}{2}\cos \theta }
100
三相三線式
3
E
I
cos
θ
{\displaystyle {\sqrt {3}EI\cos \theta }
3
E
I
3
cos
θ
{\displaystyle {\frac {\sqrt {3}EI}{3}\cos \theta }
115
三相三線式のほうが送電電力比率が大きいことが分かる[ 26]
次の手順で単相交流と三相交流の、電線の質量比較を行う。ただし同じ条件にするため、同一電力
P
[
W
]
{\displaystyle P[{\text{W}]}
E
[
V
]
{\displaystyle E[{\text{V}]}
cos
θ
{\displaystyle \cos \theta }
P
l
[
W
]
{\displaystyle P_{l}[{\text{W}]}
また、電線の長さを
l
[
km
]
{\displaystyle l[{\text{km}]}
単相交流と三相交流の電流比を求める
抵抗比を求める
電線の断面積比を求める
電線質量比を求める
単相二線式の線電流を
I
1
[
A
]
{\displaystyle I_{1}[{\text{A}]}
I
3
[
A
]
{\displaystyle I_{3}[{\text{A}]}
I
1
=
P
E
cos
θ
I
3
=
P
3
E
cos
θ
{\displaystyle {\begin{aligned}I_{1}&={\frac {P}{E\cos \theta }\\I_{3}&={\frac {P}{\sqrt {3}E\cos \theta }\\\end{aligned}
となるため、電流比は
I
3
I
1
=
P
3
E
cos
θ
P
E
cos
θ
=
1
3
{\displaystyle {\frac {I_{3}{I_{1}={\frac {\frac {P}{\sqrt {3}E\cos \theta }{\frac {P}{E\cos \theta }={\frac {1}{\sqrt {3}
となる[ 27]
単相二線式における一線あたりの抵抗を
R
1
[
Ω
]
{\displaystyle R_{1}[\Omega ]}
R
3
[
Ω
]
{\displaystyle R_{3}[\Omega ]}
P
l
=
2
R
1
I
1
2
=
3
R
3
I
3
2
{\displaystyle P_{l}=2R_{1}{I_{1}^{2}=3R_{3}{I_{3}^{2}
となるから、抵抗比は
R
3
R
1
=
2
I
1
2
2
I
3
2
=
2
3
×
3
1
=
2
{\displaystyle {\frac {R_{3}{R_{1}={\frac {2{I_{1}^{2}{2{I_{3}^{2}={\frac {2}{3}\times {\frac {3}{1}=2}
となる[ 27]
電線材料の体積抵抗率を
ρ
[
Ω
⋅
m
]
{\displaystyle \rho [\Omega \cdot {\text{m}]}
A
1
[
cm
2
]
{\displaystyle A_{1}[{\text{cm}^{2}]}
A
3
[
cm
2
]
{\displaystyle A_{3}[{\text{cm}^{2}]}
R
1
=
ρ
l
A
1
×
10
5
R
3
=
ρ
l
A
3
×
10
5
{\displaystyle {\begin{aligned}R_{1}&={\frac {\rho l}{A_{1}\times 10^{5}\\R_{3}&={\frac {\rho l}{A_{3}\times 10^{5}\\\end{aligned}
となり
A
1
=
ρ
l
R
1
×
10
5
A
3
=
ρ
l
R
3
×
10
5
{\displaystyle {\begin{aligned}A_{1}&={\frac {\rho l}{R_{1}\times 10^{5}\\A_{3}&={\frac {\rho l}{R_{3}\times 10^{5}\\\end{aligned}
となるから、断面積比は
A
3
A
1
=
ρ
l
R
3
×
10
5
ρ
l
R
1
×
10
5
=
R
1
R
3
=
1
2
{\displaystyle {\frac {A_{3}{A_{1}={\frac {\frac {\rho l}{R_{3}\times 10^{5}{\frac {\rho l}{R_{1}\times 10^{5}={\frac {R_{1}{R_{3}={\frac {1}{2}
となる[ 4]
電線材料の密度を
σ
[
kg
/
cm
3
]
{\displaystyle \sigma [{\text{kg}/{\text{cm}^{3}]}
W
1
[
kg
]
{\displaystyle W_{1}[{\text{kg}]}
W
3
[
kg
]
{\displaystyle W_{3}[{\text{kg}]}
W
1
=
2
σ
A
1
l
×
10
5
W
3
=
3
σ
A
3
l
×
10
5
{\displaystyle {\begin{aligned}W_{1}&=2\sigma A_{1}l\times 10^{5}\\W_{3}&=3\sigma A_{3}l\times 10^{5}\\\end{aligned}
となるから、重量比は
W
3
W
1
=
3
σ
A
3
l
×
10
5
2
σ
A
1
l
×
10
5
=
3
A
3
2
A
1
=
3
2
×
1
2
=
3
4
{\displaystyle {\frac {W_{3}{W_{1}={\frac {3\sigma A_{3}l\times 10^{5}{2\sigma A_{1}l\times 10^{5}={\frac {3A_{3}{2A_{1}={\frac {3}{2}\times {\frac {1}{2}={\frac {3}{4}
と求まる[ 4] [ 4]
三相交流の波形
相順
電源記号
変圧器 端子
入力
出力
第一相
R
U
u
第二相
S
V
v
第三相
T
W
w
第四相
N
O
o
本来電灯 は蛍光灯や白熱灯といった照明器具という意味[ 28] 動力 は機械を動かす力という意味で使用される[ 29]
だが、本来の意味とは異なる意味でこれらの語句が使用されることがある。ここではその例を見ていく。
電柱に設置されている配電線 のうち、三相交流を三相三線式200Vで送電している配電線を低圧動力線 と呼ぶ。
一方、単相交流を単相三線式100V/200Vで送電している配電線を低圧電灯線 と呼ぶ[ 30]
蛍光灯や白熱灯といった照明器具および単相100V・単相200Vで使用する電気機器以外の電気機器を動力 という。
三相電源で使用されるエアコンやエレベータなどが動力にあたる[ 31]
また、三相電源のことを動力電源 という[ 32]
電力会社の料金プランに電灯・動力の語句が使われることがある。
例えば北海道電力には従量電灯という料金プランが存在する。プランの適用対象は「照明器具および単相交流 で動作する電気機器を使用する場合」となっている[ 33]
また東京電力には動力プランという料金プランが存在する。プランの適用対象は三相交流 を使用する電気機器(例:大型エアコン)を使用する場合となっている[ 34]
JIS C4526-1 3.4.9全極遮断[ 35]
具体的な送電方式として、以下のような方法がある。
^ 対応する相電流とは、Δ結線のある一点から線電流が流れ出ているとき、その点に流れ込む相電流のことである。
^ 単相二線式の、1線当たりの送電電力を100%としている。
^ 三相三線式の結線方法はY結線かΔ結線として計算している
^ 送電電力比率は力率を1として計算している





































































![{\displaystyle P[{\text{W}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/980ad9ed4ac801dae9687824d17fd06532cdf62e)
![{\displaystyle E[{\text{V}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d69ac38485f969c2fcb49b0355d3fcda9ae9bcdd)
![{\displaystyle P_{l}[{\text{W}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a66c1bcae4fdb7042775a31f9bb9617b98cbbd82)
![{\displaystyle l[{\text{km}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27c5191c5b58f8e96f0571a91d2b45b5f165d866)
![{\displaystyle I_{1}[{\text{A}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a510a01bcc9149522a9f7b1e1b9054c2fc6eadee)
![{\displaystyle I_{3}[{\text{A}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/211f9ea01866e18099ac56cda0a0573269b94491)


![{\displaystyle R_{1}[\Omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4248ecb66c43388057d2455cfcd1c04ec384eeb0)
![{\displaystyle R_{3}[\Omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/302b66a502f407ae28f55724095eb94f76ff3eae)


![{\displaystyle \rho [\Omega \cdot {\text{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ffbe8a39f0155f0fe26c614cf8b1926101700b)
![{\displaystyle A_{1}[{\text{cm}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e828a40606ad4c24bc260e420b3c3ddc8866b3f)
![{\displaystyle A_{3}[{\text{cm}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5db60e5a80cc1618b7132c51afc44d28835ca9b1)



![{\displaystyle \sigma [{\text{kg}/{\text{cm}^{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71bc4efb6ac9274bd3db27bfcd202b8d4bfc0e44)
![{\displaystyle W_{1}[{\text{kg}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6488424519ca17930fa45a161389d099d390efb3)
![{\displaystyle W_{3}[{\text{kg}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0818f84564a5e60c553c5d63d7fc7b1acc7dcada)


