関手
圏論における関手(かんしゅ、英: functor)は、圏から圏への構造と両立する対応付けである。関手によって一つの数学体系から別の体系への組織的な対応が定式化される。関手は「圏の圏」における射と考えることもできる。
歴史
関手の概念の萌芽はエヴァリスト・ガロアによる群を用いた代数方程式の研究に見ることができる。
20世紀初めのエミー・ネーターらによる加群の研究において拡大加群などさまざまな関手的構成が蓄積された。
20世紀半ばの代数的位相幾何学において実際に関手が定義され、図形から様々な「自然な」代数的構造を取り出す操作を定式化するために利用された。
ここでは(基本群のような)代数的対象が位相空間から導かれ、位相空間の間の連続写像は基本群の間の代数的準同型を導いている。
その後アレクサンドル・グロタンディークらによる代数幾何学の変革の中で様々な数学的対象の関手による定式化が徹底的に追求された。
定義
共変関手
圏 C から圏 D への関手、特に共変関手(きょうへんかんしゅ、covariant functor)F は、
- C の各対象 X を D の各対象 F(X) に対応させる
- C における射 f: X → Y を D における射 F(f): F(X) → F(Y) に対応させ、以下の性質を満たす
- 各対象 X ∈ C に対して F(idX) = idF(X) ,
- 任意の射 f: X → Y および g: Y → Z に対して F(g ∘ f) = F(g) ∘ F(f).
すなわち、関手に対して恒等射および射の合成を保存することが要請される。
反変関手
関手に似た形式を持ちながら、射を反転させる(合成を逆向きにする)ような対応が多数存在する。そこで、C から D への 反変関手(はんへんかんしゅ、contravariant functor)F が、各対象 X ∈ C を 対象 F(X) ∈ D に対応させ、各射 f: X → Y ∈ C を射 F(f): F(Y) → F(X) ∈ D に対応させるとき、以下の性質
- 全ての対象 X ∈ C において F(idX) = idF(X),
- 全ての射 f: X → Y および g: Y → Z に対して F(g ∘ f) = F(f) ∘ F(g)
を満たすものとして定義される。
注意
C の双対圏 Cop を考えるならば、反変関手 F: C → D をかわりに(共変)関手 F: Cop → D(場合によっては F: C → Dop)と見ることによって、共変関手の概念だけで処理することができる。
反変関手はまれに「余関手」(よかんしゅ、cofunctor)と呼ばれることもあるが、圏論の文脈で「(圏論的)双対」(つまり「全ての矢印を逆向きにする」)を意味する接頭辞「余」の使い方とは乖離がある。(共変)関手 F は射 f: X → Y を射 F(f): F(X) → F(Y) に対応させるものだが、ここで双対を得るために全ての矢印を逆向きにするなら射 f: X ← Y に射 F(f): F(X) ← F(Y) が対応することになる。これは結局のところ普通の共変関手の概念を表している。つまり関手とは自己双対的な概念であり、字義どおりにとらえるなら余関手と関手とは同じ概念を表している。
性質
関手の公理からの重要な帰結として
の二つがあげられる。
いかなる圏 C においても、恒等関手(こうとうかんしゅ、identity functor)1C が、どの対象も射もそれ自身へうつすものとして定まる。函手 F: A → B および G: B → C に対し、それらの合成 GF: A → C を考えることができる。関手の合成は、それが定義される限り結合的である。このことから、関手が圏の圏における射となることが示される。
唯一つの対象からなる圏は、射をその元とし、合成をその演算とするようなモノイドと同値である。圏と見なしたモノイドの間の関手はモノイドの準同型に他ならない。その意味で、勝手な圏の間の関手は、モノイドの準同型の、二つ以上の対象を持つ圏へのある種の一般化になっている。
自然変換
圏として定式化された数学理論の上に関手によってさまざまな自然な構成が与えられるが、自然変換によって2つの構成を比較する「自然な準同型」が記述される。時に2つの見かけ上異なった構成が同等の概念を定めていることがあるが、この状況は2つの関手の間の自然同型になっている自然変換によってとらえられる。
F, G が圏 C と D の間の(共変)関手であるとき、F から G への自然変換 η は C に含まれる全ての対象 X に対し D の射 ηX: F(X) → G(X) を与える。このとき、C の任意の射 f: X → Y に対し、ηY ∘ F(f) = G(f) ∘ ηX が成り立つ。 これは即ち、以下の図式
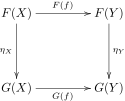
が可換になることを意味している。
函手 F から G への自然変換 η が存在して ηX が C に含まれる全ての対象 X に対して同型射となるとき、この自然変換は自然同型であるといい、F ≈η G などと書く。圏 C, D の間の関手 F: C → D, G: D → C について自然同型 GF ≈ IdC, FG ≈ IdD がともに成り立つならば C と D は同等なもの(圏同値)と見なされる(さらにこれら二つの自然同型 (≈) が厳密に等号 (=) で成り立つ圏同型を考えることもできるが、実用上これは条件として強すぎる)。
C から D への関手を対象とし、関手の間の自然変換を射とすることで関手圏 Funct(C, D) が考えられる。こうして得られる圏に図式の圏や前層の圏、層の圏がある。また、群 G が作用する集合の圏は G を圏と見なしたときの Funct(G, Sets) と同値になる[1]。
関手に対する様々な条件
以下 F: C → D を関手とする。
- 忠実関手と充満関手
- C の任意の対象 X, Y について F: HomC(X, Y) → HomD(FX, FY); f → F(f) が単射のとき F は忠実であるといい、この対応が全射のとき F は充満であるという。
- 随伴関手
- 函手 F に対して函手 G: D → C が HomD(FX, Y) ≡ HomC(X, GY) を満たすならば F は G の左随伴であると言い、 G は F の右随伴であると言う。
- 加法的関手
- 射の集合がアーベル群となっている圏(Ab-豊饒圏)の間の函手が、射の集合の間の群準同型を与えるならば加法的であると言う。
- 完全関手
- 短完全列 を短完全列に写すような関手は完全であると言い、完全関手は任意の完全系列を保つ。有限の極限のみを保つ関手は左完全、双対的に有限の余極限のみを保つ関手は右完全と言う。
表現可能関手
圏 C の対象 X について HomC(—, X) や HomC(X, —) の形にかけるような C から Sets (または C の hom-集合の構造を表すしかるべき圏)への関手は表現可能関手とよばれる。米田の補題によって表現可能関手たちとその間の自然変換はもとの圏の構造を完全に反映していることが知られる。数学のさまざまな場面で与えられた関手が表現可能であるかどうかやどんな対象によって表現されるか、あるいはその関手が表現可能になるように圏を変形できるかということが問題になる。
特定の形の図式に関する極限は図式圏への対角埋め込み関手に対する右随伴関手として定式化できる。テンソル積や対象積、交代積は多重線形写像の関手を表現するような対象として定式化できる。
例
- 自己関手
- 圏 C から同じ圏 C への関手は、自己関手(じこかんしゅ、endofunctor)と呼ばれる。恒等関手は自己関手の自明な例である。また、圏 C から、その部分圏 D への関手は、圏 C における自己関手でもある。
- 定関手
- 空でない圏 D の対象 X について、任意の圏 C から D への X が定める定関手(ていかんしゅ、constant functor)を以下のようにして構成できる: C の全ての対象を X に写し、C の全ての射を X の恒等射に写す。定関手は selection functor ともよばれる。
- 冪集合関手
- 集合の圏 Sets からそれ自身への関手 P を、各集合をその冪集合へと写し、各写像 f: X → Y を写像 X ⊃ U → f(U) ⊂ Y に写すことにより考えることができる。また写像 f: X → Y を Y ⊃ U → f−1(U) ⊂ X なる写像に対応させることで反変の冪集合関手を考えることもできる。反変版の冪集合関手は2点集合によって表現されている。
- 双対ベクトル空間
- 可換体 K 上のベクトル空間をその双対空間に対応させ、線型写像をその転置写像に対応させることで、K-ベクトル空間の圏からそれ自身への反変関手が構成できる。
- 基本群と基本亜群
- 点つき位相空間、すなわち基点を伴った位相空間の圏を考える。その対象は位相空間 X と X の固定した一点 x の組 (X, x) で、(X, x) から (Y, y) への射は f(x) = y となる(基点を基点に写す)連続写像 f: X → Y によって与えられる。
- 点つき位相空間 (X, x) に対して、基本群 π1(X, x) が x を基点とする X 内のループのホモトピー類のなす群として定義できる。f: (X, x) → (Y, y) が点つき位相空間の射ならば、X 内の x を基点とした全ての閉道は、y を基点とする Y 内の閉道に写される。この操作はホモトピー同値と閉道の合成とに両立するから π(X, x) から π(Y, y) への群の準同型写像を得る。ここから、点つき位相空間の圏から群の圏への関手が得られる。
- 基点を特に指定しない位相空間の圏では一般のパスについて(端点を固定した)ホモトピー類を考えることができる。こうして位相空間の圏から小さな圏の圏への共変関手である基本亜群 Π が得られるが、これは X のそれぞれの点を基点にして得られる基本群と、パスの合成によって与えられる基点の取り替えを表現していると見なせる。連続写像 f: X → Y に対応する射 Π は函手 ΠX → ΠY になっている。
- 導来関手
- アーベル圏の上の(コ)ホモロジー的関手はしばしば片側完全関手の導来関手として定式化される。
- 忘却関手と自由関手
- C が、D の対象のうちでさらに付加的な構造を持つものの圏として定式化されているとき、C の対象の付加的な構造を無視することで C から D への忘却関手(ぼうきゃくかんしゅ、forgetful functor)を考えることができる。忘却関手の左随伴関手になっているような関手は自由関手(じゆうかんしゅ、free functor)とよばれる。
- 非常に単純な忘却関手として、アーベル群の交換法則を無視する忘却関手から群が得られ、群から逆元を無視してモノイドが、モノイドから単位元を無視して半群が得られるような忘却関手が挙げられる。
- また、複素数体上のベクトル空間の圏において、各ベクトル空間を単に集合と見なし、各線型写像を単に集合間の写像と見なして集合の圏への忘却関手を構成できる。各集合に対してその元の形式的な線型結合の空間を考えることで、この忘却関手に体する左随伴関手が構成される。
- 定数関数環
- 位相空間とその間の連続写像を射とする圏から実結合的多元環の圏への反変関手が、各位相空間 X に対してその上の実数値連続関数全体の成す多元環 C(X) を対応させることによって定まる。各連続写像 f: X → Y は各 φ ∈ C(Y) に対して C(f)(φ) ≔ φ ∘ f と置くことにより、多元環の準同型 C(f): C(Y) → C(X) を引き起こす。
- 接関手と余接関手
- 可微分多様体をその接ベクトル束へうつし、滑らかな写像をその微分にうつす写像は、可微分多様体の圏からベクトル束の圏への共変関手である。同様に、可微分多様体をその余接ベクトル束へうつし、滑らかな写像をその引き戻しへうつす写像は反変関手を定める。
- これらの構成を点ごとで考えると、基点付き可微分多様体の圏から実ベクトル空間の圏への共変および反変関手が得られる。
- リー環構成
- 実または複素リー群に対して、その付随する実または複素リー環を対応付けることで関手が定まる。
- テンソル積構成
- C をある固定された体上のベクトル空間の圏で、その射として線型写像をとるとき、テンソル積 V ⊗ W は、どちらの引数に関しても共変な関手 C × C → C を定める。
関連項目
脚注
外部リンク
- Weisstein, Eric W. "Functor". mathworld.wolfram.com (英語).
- Barile, Margherita. "Covariant Functor". mathworld.wolfram.com (英語).
- Barile, Margherita. "Contravariant Functor". mathworld.wolfram.com (英語).
- functor - PlanetMath.
- Hazewinkel, Michiel, ed. (2001), “Functor”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- functor in nLab