(3,4)-원환면 매듭. 위 그림:
(3,4)-원환면 매듭. 위 그림:  를
를  와 붙이고,
와 붙이고,  를
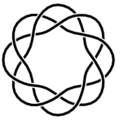
를  와 붙이면 이는 원환면을 이루며, 푸른 선들은 그 위의 원환면 매듭을 이룬다. 아래 그림: 같은 원환면 매듭을 꼬임으로 표현한 것.
와 붙이면 이는 원환면을 이루며, 푸른 선들은 그 위의 원환면 매듭을 이룬다. 아래 그림: 같은 원환면 매듭을 꼬임으로 표현한 것.
매듭 이론에서 원환면 연환(圓環面連環, 영어: torus link)은 원환면 위에 간단하게 그려질 수 있는 연환이다.
정의
0이 아닌 두 정수  가 주어졌다고 하자. 그렇다면,
가 주어졌다고 하자. 그렇다면,  -원환면 연환은 다음과 같은 3차원 곡선들의 집합으로 주어지는 연환이다.
-원환면 연환은 다음과 같은 3차원 곡선들의 집합으로 주어지는 연환이다.



이 곡선들은 원환면

위에 속하는 연환을 정의한다.
즉, 이는 원환면을 다음과 같이 감는다.
- z축에 대하여,
 번 감기
번 감기
- 원환면의 중심에 있는 원에 대하여,
 번 감기
번 감기
매듭인 원환면 연환을 원환면 매듭(영어: torus knot)이라고 한다.
성질
 -원환면 연환의 연결 성분의 수는
-원환면 연환의 연결 성분의 수는

이다. 즉, 이것이 원환면 매듭이 될 필요 충분 조건은  와
와  가 서로소인 것이다.
가 서로소인 것이다.
 -원환면 연환이 자명한 매듭일 필요 충분 조건은 다음과 같다.
-원환면 연환이 자명한 매듭일 필요 충분 조건은 다음과 같다.
 이거나
이거나  이다. 즉,
이다. 즉,  이다.
이다.
 -원환면 연환과
-원환면 연환과  -원환면 연환이 동치일 필요 충분 조건은 다음과 같다.
-원환면 연환이 동치일 필요 충분 조건은 다음과 같다.
 이거나, 또는
이거나, 또는 
즉, 자명한 매듭이 아닌 경우 항상

인 표준형으로 놓을 수 있다.
또한,  -원환면 연환의 거울 대칭 연환은
-원환면 연환의 거울 대칭 연환은  -원환면 연환이다.
-원환면 연환이다.
교차수
 -원환면 연환의 교차수는 다음과 같다.
-원환면 연환의 교차수는 다음과 같다.

예
-
(1,±1)-원환면 매듭 (
자명한 매듭 0
1)
-
(2,±2)-원환면 연환 (
호프 연환 
)
-
(3,2)-원환면 매듭 (오른손
세잎매듭 3
1)
-
(3,−2)-원환면 매듭 (왼손
세잎매듭 3
1)
-
(3,±3)-원환면 연환 (

)
-
(5,2)-원환면 매듭 (오른손 다섯잎매듭 51)
-
(5,−2)-원환면 매듭 (왼손 다섯잎매듭 51)
-
(8,2)-원환면 연환

-
(8,−2)-원환면 연환

-
(7,−2)-원환면 매듭 (71)
-
(7,−3)-원환면 매듭
-
(8,−3)-원환면 매듭
-
(8,3)-원환면 매듭
-
(12,2)-원환면 연환
이 밖에도, 원환면 매듭의 알렉산더-브리그스 기호 및 (연환의 경우) 시슬스웨이트 기호는 다음과 같다.
| (p,q) |
2 |
3
|
| 2
|
호프 연환  (L2a1) (L2a1)
|
| 3
|
세잎매듭 31 |
 (L6n1) (L6n1)
|
| 4
|
솔로몬 연환  (L4a1) (L4a1) |
819
|
| 5
|
다섯잎매듭 51 |
10124
|
외부 링크