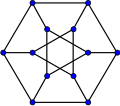
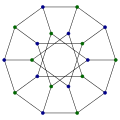
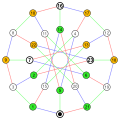
그래프 이론 에서 일반화 페테르센 그래프 (一般化Petersen graph, 영어 : generalized Petersen graph )는 같은 수의 꼭짓점을 갖는 정다각형과 별 모양에서 대응하는 꼭짓점들을 이어 얻는 그래프 이다. 특히, 오각형과 오각 별을 이어 얻는 그래프를 페테르센 그래프 (영어 : Petersen graph )라고 한다.[ 1]
3 이상의 정수
n
≥
3
{\displaystyle n\geq 3}
n
{\displaystyle n}
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
n
∤
k
{\displaystyle n\nmid k}
n
{\displaystyle n}
n
/
2
∤
k
{\displaystyle n/2\nmid k}
일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
그래프 이다.
V
(
GPG
(
n
,
k
)
)
=
{
u
i
,
v
i
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}
E
(
GPG
(
n
,
k
)
)
=
{
u
i
u
i
+
1
,
u
i
v
i
,
v
i
v
i
+
k
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}
여기서 첨자는 법
n
{\displaystyle n}
u
n
+
i
=
u
i
{\displaystyle u_{n+i}=u_{i}
v
n
+
i
=
u
i
{\displaystyle v_{n+i}=u_{i}
u
i
v
i
{\displaystyle u_{i}v_{i}
바큇살 (영어 : spoke )이라고 한다.
당연히
GPG
(
n
,
k
)
=
GPG
(
n
,
k
+
n
)
=
GPG
(
n
,
−
k
)
{\displaystyle \operatorname {GPG} (n,k)=\operatorname {GPG} (n,k+n)=\operatorname {GPG} (n,-k)}
이므로, 보통
1
≤
k
<
n
/
2
{\displaystyle 1\leq k<n/2}
를 가정한다.
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
완벽 부합 일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
2
n
{\displaystyle 2n}
3
n
{\displaystyle 3n}
삼차 그래프 이며, 완벽 부합 을 갖는다. 구체적으로, 위와 같은 표기에서,
{
u
i
v
i
}
i
∈
Z
/
n
{\displaystyle \{u_{i}v_{i}\}_{i\in \mathbb {Z} /n}
완벽 부합 을 이룬다.
임의의 정수
n
≥
3
{\displaystyle n\geq 3}
1
≤
k
,
k
′
<
n
/
2
{\displaystyle 1\leq k,k'<n/2}
동치 이다.[ 2] :Proposition 9 [ 3]
GPG
(
n
,
k
)
≅
GPG
(
n
,
k
′
)
{\displaystyle \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,k')}
k
k
′
≡
±
1
(
mod
n
)
{\displaystyle kk'\equiv \pm 1{\pmod {n}
예를 들어,
GPG
(
7
,
2
)
≅
GPG
(
7
,
3
)
{\displaystyle \operatorname {GPG} (7,2)\cong \operatorname {GPG} (7,3)}
일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
안둘레 는 항상
min
{
8
,
k
+
3
,
n
/
gcd
{
n
,
k
}
}
{\displaystyle \min\{8,k+3,n/\gcd\{n,k\}\}
[ 4] :Theorem 2.1
증명:
일반화 페테르센 그래프의 꼭짓점 및 변은
V
(
GPG
(
n
,
k
)
)
=
{
u
i
,
v
i
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}
E
(
GPG
(
n
,
k
)
)
=
{
u
i
u
i
+
1
,
u
i
v
i
,
v
i
v
i
+
k
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}
이다. 그 속에서
u
0
−
v
0
−
v
k
−
u
k
−
u
k
+
1
−
v
k
+
1
−
v
1
−
u
1
−
u
0
{\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k+1}-v_{k+1}-v_{1}-u_{1}-u_{0}
는 길이 8의 순환 이며,
u
0
−
v
0
−
v
k
−
u
k
−
u
k
−
1
−
⋯
−
u
1
−
u
0
{\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k-1}-\dotsb -u_{1}-u_{0}
는 길이
k
+
3
{\displaystyle k+3}
순환 이며,
v
0
−
v
k
−
v
2
k
−
⋯
−
v
0
{\displaystyle v_{0}-v_{k}-v_{2k}-\dotsb -v_{0}
는 길이
n
/
gcd
{
n
,
k
}
{\displaystyle n/\gcd\{n,k\}
순환 이다.
또한, 다음이 성립한다.
girth
(
GPG
(
a
k
±
b
,
k
)
)
≤
a
+
b
+
2
{\displaystyle \operatorname {girth} (\operatorname {GPG} (ak\pm b,k))\leq a+b+2}
증명:
일반화 페테르센 그래프의 꼭짓점 및 변은
V
(
GPG
(
n
,
k
)
)
=
{
u
i
,
v
i
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}
E
(
GPG
(
n
,
k
)
)
=
{
u
i
u
i
+
1
,
u
i
v
i
,
v
i
v
i
+
k
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}
이다. 그 속에서
u
0
−
v
0
−
v
k
−
⋯
−
v
a
k
≡
±
b
−
u
±
b
−
u
±
(
b
−
1
)
−
⋯
−
u
±
1
−
u
0
{\displaystyle u_{0}-v_{0}-v_{k}-\dotsb -v_{ak\equiv \pm b}-u_{\pm b}-u_{\pm (b-1)}-\dotsb -u_{\pm 1}-u_{0}
은 길이
a
+
b
+
2
{\displaystyle a+b+2}
복부호 동순 ).
위 상계 가운데 적어도 하나가 포화된다. 즉, 만약
1
≤
k
<
n
/
2
{\displaystyle 1\leq k<n/2}
k
=
min
{
1
≤
k
′
<
n
/
2
:
GPG
(
n
,
k
)
≅
GPG
(
n
,
k
′
)
}
{\displaystyle k=\min \left\{1\leq k'<n/2\colon \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,k')\right\}
일 때, 일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
안둘레 는 다음 표에서, 위에서부터 가장 먼저 해당하는 행에 의해 주어진다.[ 4] :Theorem 2.8
조건
안둘레
n
=
3
k
{\displaystyle n=3k}
3
n
=
4
k
{\displaystyle n=4k}
4
k
=
1
{\displaystyle k=1}
n
=
5
k
{\displaystyle n=5k}
5
n
=
5
k
/
2
{\displaystyle n=5k/2}
k
=
2
{\displaystyle k=2}
n
=
6
k
{\displaystyle n=6k}
6
k
=
3
{\displaystyle k=3}
n
=
2
k
+
2
{\displaystyle n=2k+2}
n
=
7
k
{\displaystyle n=7k}
7
n
=
7
k
/
2
{\displaystyle n=7k/2}
n
=
7
k
/
3
{\displaystyle n=7k/3}
k
=
4
{\displaystyle k=4}
n
=
2
k
+
3
{\displaystyle n=2k+3}
n
=
3
k
±
2
{\displaystyle n=3k\pm 2}
그 밖의 경우
8
증명:
일반화 페테르센 그래프의 꼭짓점 및 변은
V
(
GPG
(
n
,
k
)
)
=
{
u
i
,
v
i
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {V} (\operatorname {GPG} (n,k))=\{u_{i},v_{i}\colon i\in \mathbb {Z} /n\}
E
(
GPG
(
n
,
k
)
)
=
{
u
i
u
i
+
1
,
u
i
v
i
,
v
i
v
i
+
k
:
i
∈
Z
/
n
}
{\displaystyle \operatorname {E} (\operatorname {GPG} (n,k))=\{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\colon i\in \mathbb {Z} /n\}
이다. 일반화 페테르센 그래프 속의 모든 순환 은 당연히 짝수 개의 바큇살
u
i
v
i
{\displaystyle u_{i}v_{i}
모든 일반화 페테르센 그래프는 4개의 바큇살을 갖는 길이 8의 순환
u
0
−
v
0
−
v
k
−
u
k
−
u
k
+
1
−
v
k
+
1
−
v
1
−
u
1
−
u
0
{\displaystyle u_{0}-v_{0}-v_{k}-u_{k}-u_{k+1}-v_{k+1}-v_{1}-u_{1}-u_{0}
을 가지며, 바큇살 6개 이상의 순환의 길이는 항상 12 이상이다. 따라서, 2개의 바큇살 및 0개의 바큇살을 갖는 순환들만 고려하면 된다.
2개의 바큇살을 갖는 순환은 (편의상 첫 변을
u
0
−
u
1
{\displaystyle u_{0}-u_{1}
u
0
−
u
1
−
⋯
−
u
b
−
v
b
−
v
b
±
k
−
v
b
±
2
k
−
⋯
−
v
b
±
a
k
−
u
0
{\displaystyle u_{0}-u_{1}-\dotsb -u_{b}-v_{b}-v_{b\pm k}-v_{b\pm 2k}-\dotsb -v_{b\pm ak}-u_{0}
이것이 존재하기 위해서는
a
k
±
b
∣
n
{\displaystyle ak\pm b\mid n}
a
+
b
+
2
{\displaystyle a+b+2}
k
{\displaystyle k}
a
k
+
b
=
n
{\displaystyle ak+b=n}
a
k
+
b
=
0
{\displaystyle ak+b=0}
a
k
+
b
=
0
{\displaystyle ak+b=0}
(
a
,
b
)
=
(
1
,
−
k
)
{\displaystyle (a,b)=(1,-k)}
k
+
3
{\displaystyle k+3}
a
k
+
b
=
n
{\displaystyle ak+b=n}
만약
n
=
a
k
±
1
{\displaystyle n=ak\pm 1}
GPG
(
n
,
k
)
≅
GPG
(
n
,
a
)
{\displaystyle \operatorname {GPG} (n,k)\cong \operatorname {GPG} (n,a)}
k
{\displaystyle k}
만약
n
=
a
k
{\displaystyle n=ak}
a
{\displaystyle a}
만약
n
=
2
k
−
b
{\displaystyle n=2k-b}
k
≥
n
/
2
{\displaystyle k\geq n/2}
위 경우를 제외하면, 이러한 순환의 길이가 8 미만인 경우는 남는 것은
(
a
,
b
)
=
(
2
,
2
)
,
(
2
,
3
)
,
(
3
,
2
)
,
(
3
,
−
2
)
{\displaystyle (a,b)=(2,2),(2,3),(3,2),(3,-2)}
0개의 바큇살을 갖는 순환은
u
i
{\displaystyle u_{i}
v
i
{\displaystyle v_{i}
u
i
{\displaystyle u_{i}
n
{\displaystyle n}
v
i
{\displaystyle v_{i}
n
/
gcd
{
n
,
k
}
{\displaystyle n/\gcd\{n,k\}
후자의 길이가 7 이하가 되려면, 가능한 경우는
n
/
k
∈
{
3
/
1
,
4
/
1
,
5
/
1
,
5
/
2
,
6
/
1
,
7
/
1
,
7
/
2
,
7
/
3
}
{\displaystyle n/k\in \{3/1,4/1,5/1,5/2,6/1,7/1,7/2,7/3\}
나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
대칭군
Sym
(
4
)
{\displaystyle \operatorname {Sym} (4)}
케일리 그래프 이다. 일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
동치 이다.[ 5]
어떤 유한군 의 케일리 그래프 와 동형이다.
k
2
≡
1
(
mod
n
)
{\displaystyle k^{2}\equiv 1{\pmod {n}
예를 들어, 나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
5
2
≡
1
(
mod
12
)
{\displaystyle 5^{2}\equiv 1{\pmod {12}
대칭군
Sym
(
4
)
{\displaystyle \operatorname {Sym} (4)}
케일리 그래프 이다. 마찬가지로, 각기둥 그래프
GPG
(
n
,
1
)
{\displaystyle \operatorname {GPG} (n,1)}
2
n
{\displaystyle 2n}
정이면체군
Dih
(
n
)
{\displaystyle \operatorname {Dih} (n)}
케일리 그래프 이다. 반면, 페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
케일리 그래프 가 아니다.
일반화 페테르센 그래프는 삼차 그래프 이므로, 브룩스 정리(영어 : Brooks’ theorem )에 의하여 그 색칠수 는 2 또는 3이다.
일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
동치 이다.
이분 그래프 이다. (즉, 색칠수 가 2이다.)
n
{\displaystyle n}
k
{\displaystyle k}
다시 말해, 일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
색칠수 는 다음과 같다.
χ
(
GPG
(
n
,
k
)
)
=
{
2
2
∣
n
∧
2
∤
k
3
2
∤
n
∨
2
∣
k
{\displaystyle \chi (\operatorname {GPG} (n,k))={\begin{cases}2&2\mid n\land 2\nmid k\\3&2\nmid n\lor 2\mid k\end{cases}
여기서
∧
{\displaystyle \land }
논리곱 (AND),
∨
{\displaystyle \lor }
논리합 (OR)이다. 예를 들어, 페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
색칠수 는 3이다.
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
의 3색
그래프 색칠
데자르그 그래프
GPG
(
10
,
3
)
{\displaystyle \operatorname {GPG} (10,3)}
의 2색
그래프 색칠
뒤러 그래프
GPG
(
6
,
2
)
{\displaystyle \operatorname {GPG} (6,2)}
의 3색
그래프 색칠
페테르센 그래프의 변 색칠수 는 4이다.[ 6] 변 색칠수 가 4 이상인 가장 작은 삼차 그래프 이다. 반면, 페테르센 그래프가 아닌 다른 모든 일반화 페테르센 그래프의 변 색칠수 는 3이다.[ 7]
일반화 페테르센 그래프
GPG
(
9
,
2
)
{\displaystyle \operatorname {GPG} (9,2)}
순열 을 무시하면) 유일한 3색 변 색칠 을 갖는다.
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
의 4색
변 색칠
뒤러 그래프
GPG
(
6
,
2
)
{\displaystyle \operatorname {GPG} (6,2)}
의 3색
변 색칠
정십이면체 그래프
GPG
(
10
,
2
)
{\displaystyle \operatorname {GPG} (10,2)}
의 3색
변 색칠
데자르그 그래프
GPG
(
10
,
3
)
{\displaystyle \operatorname {GPG} (10,3)}
의 3색
변 색칠
나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
의 3색
변 색칠
임의의 일반화 페테르센 그래프
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
3
≤
n
{\displaystyle 3\leq n}
1
≤
k
<
n
/
2
{\displaystyle 1\leq k<n/2}
[ 8]
(가) 해밀턴 순환 을 갖는다.
(나)
n
≡
5
(
mod
6
)
{\displaystyle n\equiv 5{\pmod {6}
k
∈
{
2
,
(
n
−
1
)
/
2
}
{\displaystyle k\in \{2,(n-1)/2\}
또한, (나)의 경우, 임의의 꼭짓점을 제거하면 이는 해밀턴 순환 을 갖는다. (특히, 모든 일반화 페테르센 그래프는 항상 해밀턴 경로 를 갖는다.)
예를 들어, 페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
해밀턴 경로 를 가지지만, (나)의 경우에 해당하므로 해밀턴 순환 을 가지지 못한다.
뒤러 그래프
GPG
(
6
,
2
)
{\displaystyle \operatorname {GPG} (6,2)}
속의
해밀턴 순환 . 맨 밖의 변들이
해밀턴 순환 을 이룬다.
일반화 페테르센 그래프
GPG
(
8
,
3
)
{\displaystyle \operatorname {GPG} (8,3)}
속의
해밀턴 순환 . 맨 밖의 변들이
해밀턴 순환 을 이룬다.
일반화 페테르센 그래프
GPG
(
9
,
2
)
{\displaystyle \operatorname {GPG} (9,2)}
속의
해밀턴 순환 . 해밀턴 순환에 속하는 변들은 굵게 칠해졌다.
정십이면체 그래프
GPG
(
10
,
2
)
{\displaystyle \operatorname {GPG} (10,2)}
속의
해밀턴 순환 . 해밀턴 순환에 속하는 변들은 붉은 색으로 굵게 칠해졌다.
나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
속의
해밀턴 순환 . 맨 밖의 변들이
해밀턴 순환 을 이룬다.
각기둥 그래프인 일반화 페테르센 그래프
GPG
(
n
,
1
)
{\displaystyle \operatorname {GPG} (n,1)}
평면 그래프 이다. 즉, 그래프 교차수 가 0이다.
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
그래프 교차수 는 2이다. 나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
그래프 교차수 는 8이다. 특히, 이 두 그래프 둘 다 평면 그래프 가 아니다.
평면 그래프 가 아닌 모든 그래프는 완전 그래프
K
5
{\displaystyle K_{5}
완전 이분 그래프
K
3
,
3
{\displaystyle K_{3,3}
그래프 마이너 로 가지는데, 페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
그래프 마이너 로 갖는다.
오각기둥 그래프
GPG
(
5
,
1
)
{\displaystyle \operatorname {GPG} (5,1)}
의 교차수는 0이다.
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
의 교차수는 2이다.
나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
의 교차수는 8이다.
일부 일반화 페테르센 그래프는 다음과 같은 특별한 이름을 갖는다.
페테르센 그래프 는 일반화 페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
완전 그래프
K
5
{\displaystyle K_{5}
선 그래프 의 여 그래프 와 동형이다.뒤러 그래프 (영어 : Dürer graph )는 일반화 페테르센 그래프
GPG
(
6
,
2
)
{\displaystyle \operatorname {GPG} (6,2)}
일반화 페테르센 그래프
GPG
(
10
,
2
)
{\displaystyle \operatorname {GPG} (10,2)}
정십이면체 의 꼭짓점 및 변들로 구성된 그래프와 같다.
데자르그 그래프 (영어 : Desargues graph )는 일반화 페테르센 그래프
GPG
(
10
,
3
)
{\displaystyle \operatorname {GPG} (10,3)}
일반화 페테르센 그래프
GPG
(
n
,
1
)
{\displaystyle \operatorname {GPG} (n,1)}
n
{\displaystyle n}
각기둥 의 꼭짓점 및 변들로 구성된 그래프와 같다.
일반화 페테르센 그래프
GPG
(
3
,
1
)
{\displaystyle \operatorname {GPG} (3,1)}
일반화 페테르센 그래프 (정육면체 그래프)
GPG
(
4
,
1
)
{\displaystyle \operatorname {GPG} (4,1)}
일반화 페테르센 그래프
GPG
(
5
,
1
)
{\displaystyle \operatorname {GPG} (5,1)}
페테르센 그래프
GPG
(
5
,
2
)
{\displaystyle \operatorname {GPG} (5,2)}
일반화 페테르센 그래프
GPG
(
6
,
1
)
{\displaystyle \operatorname {GPG} (6,1)}
뒤러 그래프
GPG
(
6
,
2
)
{\displaystyle \operatorname {GPG} (6,2)}
일반화 페테르센 그래프
GPG
(
7
,
1
)
{\displaystyle \operatorname {GPG} (7,1)}
일반화 페테르센 그래프
GPG
(
8
,
1
)
{\displaystyle \operatorname {GPG} (8,1)}
정십이면체 그래프
GPG
(
10
,
2
)
{\displaystyle \operatorname {GPG} (10,2)}
데자르그 그래프
GPG
(
10
,
3
)
{\displaystyle \operatorname {GPG} (10,3)}
일반화 페테르센 그래프
GPG
(
12
,
4
)
{\displaystyle \operatorname {GPG} (12,4)}
나우루 그래프
GPG
(
12
,
5
)
{\displaystyle \operatorname {GPG} (12,5)}
알브레히트 뒤러 의 판화 《멜란콜리아 1》데자르그의 정리에 등장하는 작도. 10개의 점
(
A
,
B
,
C
,
A
′
,
B
′
,
C
′
,
P
,
Q
,
R
,
S
)
{\displaystyle (A,B,C,A',B',C',P,Q,R,S)}
(
a
,
b
,
c
,
a
′
,
b
′
,
c
′
,
p
,
q
,
r
,
s
)
{\displaystyle (a,b,c,a',b',c',p,q,r,s)}
GPG
(
10
,
3
)
{\displaystyle \operatorname {GPG} (10,3)}
나우루의 국기 독일의 판화가 알브레히트 뒤러 의 1514년 판화 《멜란콜리아 1》(독일어 : Melancholia Ⅰ )에는 다면체 가 등장하는데, 그 꼭짓점과 변으로 구성된 그래프 는 뒤러 그래프이다.
1898년에 덴마크의 수학자 율리우스 페테르센 이 이 그래프를 다룬 3쪽의 논문을 출판하였으며,[ 9] :227, Fig. 5
연결 삼차 그래프 가운데, 임의의 변을 제거하더라도 연결 그래프 로 남는 것들의 경우, 모두 변 색칠수 가 3 이하이다.“데자르그 그래프”라는 이름은 프랑스의 수학자 지라르 데자르그 의 이름을 딴 것이다. 데자르그가 연구한 사영기하학 의 한 정리에서 등장하는 작도에서, 각 직선과 각 점에 그래프 꼭짓점을 대응시키며, 서로 인접하는 점과 직선(에 대응하는 두 꼭짓점) 사이를 변으로 이으면, 이는 데자르그 그래프가 된다.
해럴드 스콧 맥도널드 콕서터 는 1950년에 일반화 페테르센 그래프를 도입하였다.[ 10] :418, §2
GPG
(
n
,
k
)
{\displaystyle \operatorname {GPG} (n,k)}
{
n
}
+
{
n
/
k
}
{\displaystyle \{n\}+\{n/k\}
1969년에 마크 왓킨스(영어 : Mark E. Watkins )가 이 그래프 족을 “일반화 페테르센 그래프”(영어 : generalized Petersen graph )라고 명명하였다.[ 11]
“나우루 그래프”(영어 : Nauru graph )라는 이름은 데이비드 아서 엡스타인(영어 : David Arthur Eppstein )이 도입하였으며, 이 그래프의 구성에 등장하는 12각 별 모양이 나우루의 국기 에 등장하는 별과 흡사하기 때문에 붙여졌다.
↑ Holton, D. A.; Sheehan, J. (1993). 《The Petersen graph》 . Cambridge University Press. doi :10.2277/0521435943 . ISBN 0-521-43594-3 ↑ Boben, Marko; Pisanski, Tomaž; Žitni, Arjana (2005년 11월). “I-graphs and the corresponding configurations” (PDF) . 《Journal of Combinatorial Designs》 (영어) 13 (6): 406–424. doi :10.1002/jcd.20054 . 2018년 7월 23일에 원본 문서 (PDF) 에서 보존된 문서. 2017년 7월 5일에 확인함 . ↑ Steimle, Alice; Staton, William (2009년 1월 6일). “The isomorphism classes of the generalized Petersen graphs”. 《Discrete Mathematics》 (영어) 309 (1): 231–237. doi :10.1016/j.disc.2007.12.074 . ↑ 가 나 Ferrero, Daniela; Hanusch, Sarah (2014). “Component connectivity of generalized Petersen graphs” (PDF) . 《International Journal of Computer Mathematics》 (영어) 91 (9): 1940–1963. doi :10.1080/00207160.2013.878023 . ISSN 0020-7160 . 2018년 10월 20일에 원본 문서 (PDF) 에서 보존된 문서. 2017년 7월 5일에 확인함 . ↑ Nedela, Roman; Škoviera, Martin (1995년 1월). “Which generalized petersen graphs are Cayley graphs?” . 《Journal of Graph Theory》 (영어) 19 (1): 1–11. doi :10.1002/jgt.3190190102 . ↑ Naserasr, Reza; Škrekovski, Riste (2003년 7월 6일). “The Petersen graph is not 3-edge-colorable—a new proof”. 《Discrete Mathematics》 (영어) 268 (1–3): 325–326. doi :10.1016/S0012-365X(03)00138-9 . ↑ Castagna, Frank; Prins, Geert Caleb Ernst (1972). “Every generalized Petersen graph has a Tait coloring”. 《Pacific Journal of Mathematics》 (영어) 40 (1). doi :10.2140/pjm.1972.40.53 . ISSN 0030-8730 . MR 304223 . Zbl 0236.05106 . ↑ Alspach, Brian R. (1983). “The classification of Hamiltonian generalized Petersen graphs”. 《Journal of Combinatorial Theory B》 (영어) 34 : 293–312. doi :10.1016/0095-8956(83)90042-4 . MR 0714452 . ↑ Petersen, Julius Peter Christian (1898). “Sur le théorème de Tait” . 《L’Intermédiaire des Mathématiciens》 (프랑스어) 5 : 225–227. ↑ Coxeter, Harold Scott MacDonald (1950). “Self-dual configurations and regular graphs”. 《Bulletin of the American Mathematical Society》 (영어) 56 (5): 413–455. doi :10.1090/S0002-9904-1950-09407-5 . ↑ Watkins, Mark E. (1969). “A theorem on Tait colorings with an application to the generalized Petersen graphs”. 《Journal of Combinatorial Theory》 (영어) 6 : 152–164. doi :10.1016/S0021-9800(69)80116-X .
“Petersen graph” . 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4 Weisstein, Eric Wolfgang. “Generalized Petersen graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Petersen graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Desargues graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Nauru graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Dürer graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Möbius–Kantor graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Dodecahedral graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Weisstein, Eric Wolfgang. “Prism graph” . 《Wolfram MathWorld 》 (영어). Wolfram Research. Eppstein, David Arthur (2007년 12월 12일). “The many faces of the Nauru graph” . 《11011110》 (영어). Dobson, Edward (2011년 5월 9일). “The isomorphism classes of all generalized Petersen graphs” (PDF) (영어). 프리모르스카 대학교(슬로베니아어 : Univerza na Primorskem ) 세미나. 
일반화 페테르센 그래프 속의 해밀턴 순환. 해밀턴 순환에 속하는 변들은 굵게 칠해졌다.
정십이면체 그래프 속의 해밀턴 순환. 해밀턴 순환에 속하는 변들은 붉은 색으로 굵게 칠해졌다.
오각기둥 그래프 의 교차수는 0이다.
페테르센 그래프 의 교차수는 2이다.
나우루 그래프 의 교차수는 8이다.
일반화 페테르센 그래프
일반화 페테르센 그래프 (정육면체 그래프)
페테르센 그래프
일반화 페테르센 그래프
뒤러 그래프
일반화 페테르센 그래프
일반화 페테르센 그래프
정십이면체 그래프
데자르그 그래프
일반화 페테르센 그래프
나우루 그래프
