Calculus differentialis

Calculus differentialis in mathematica est ramus calculi qui proportiones per quas quantitates mutantur investigat. Qui est una ex binis traditionalibus calculi infinitesimalis partibus, quarum alia est calculus integralis.
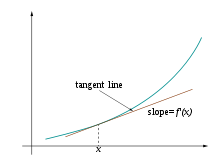
Prima proposita studii in calculo differentiali sunt derivativi functionis, notiones cognatae sicut differentiales, et eorum adhibitiones. Derivativus functionis per electam initus valorem proportionem functionis mutatae prope illam valorem initus describit. Ratio derivativi inveniendi differentiatio appellatur. In geometria, derivativus puncti est gradiens lineae tangentis ad graphum functionis ad illum punctum, dummodo derivativus existat et ad illum punctum definiatur. Pro functione valoris realis unius variabilis realis, derivativus functionis ad punctum plerumque optimam approximationem linearem functionis ad illum punctum determinat.
Calculus differentialis et calculus integralis in theoremate fundamentali calculi coniunguntur, quae dicit differentiationem esse contrarium integrationis.
Derivativi ad maxima et minima functionis invenienda saepe adhibentur. Aequationes quae derivativos implicant aequationes differentiales appellantur et fundamentales in phaenomenis naturalibus describendis sunt. Derivativi et eorum generalizationes in multis mathematicae ramis inveniuntur, inter quos sunt enodatio complexa, enodatio functionalis, geometria differentialis, ratio mensuralis, et algebra abstracta.
Nexus interni
- Derivativum
- Functio differentiabilis
- Godefridus Guilielmus Leibnitius
- Isaacus Newtonus
- Differentiale (calculus)
- Differentiatio numerica
- Geometria differentialis
Bibliographia
- Euleri, Leonardo 1755 Institutiones calculi differentialis nexus[nexus deficit]
- Caraffa, Andreas 1845 Principia calculi differentialis et integralis itemque calculi differentiarum finitarum Tipis Marini Google Books
- Cartan, Henri. 1974. Differentialrechnung. Mannheim: Bibliographisches Institut. ISBN 3411014423.
- Cartan, Henri. 1974. Differentialformen. Mannheim: Bibliographisches Institut. ISBN 3411014431.
- Edwards, J. 1892. Differential Calculus. Londinii: Macmillan and Co. Google Books.
- Field, Mike. 1976. Differential calculus and its applications. Novi Eboraci: Van Nostrand Reinhold. ISBN 0442301391, ISBN 0442301405.
- Keller, Hans Heinrich. 1974. Differential calculus in locally convex spaces. Berolini et Novi Eboraci: Springer-Verlag. ISBN 0387069623.
- Rideau, François. 1979. Exercices de calcul différentiel. Lutetiae: Hermann. ISBN 2705658629.
- Ver Eecke, Paul. 1983. Fondements du calcul différentiel. Lutetiae: Presses universitaires de France. ISBN 2130381804.
Nexus externi
| Vicimedia Communia plura habent quae ad calculum differentialem spectant. |