Krumning
Krumning er et mål for hvor mye en kurve eller en flate avviker fra en rett linje eller et todimensjonal plan. Rom med høyere dimensjoner kan også ha en krumning som er beskrevet ved tensorregning. Den spiller en sentral rolle i Einsteins generelle relativitetsteori som viser at krumningen av vårt tidrom er bestemt av masse og energi som det inneholder.
Størrelsen av krumningen til en kurve, er gitt ved hvor raskt dens tangentvektor forandrer seg. For en rett linje har denne en konstant retning som gjør det naturlig å si at den har null krumning. Derimot vil tangentvektoren til en sirkel variere jevnt rundt dens omkrets og desto raskere jo mindre dens radius r er. Derfor kan man ta størrelsen 1/r som et mål for krumningen. Da en rett linje kan betraktes som grensen av en sirkel med uendelig stor radius, vil denne definisjonen være konsistent med at linjen ikke er krummet.
Definisjon
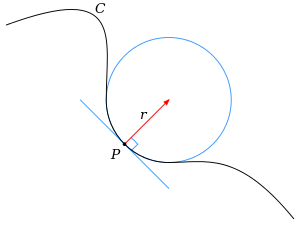
For en vilkårlig kurve vil tangentvektoren generelt forandre retning med ulik hastighet på forskjellige steder. Krummingen i et bestemt punkt kan en finne fra den sirkelen som tangerer punktet som avviker minst fra kurven i nærheten av punktet. Denne sirkelen blir kalt for krummingssirkelen eller den oskulerande sirkelen. Sentrumet i denne sirkelen er kurvens krumningssenter. Hvis den har radius r, sier man at kurven har krumning 1/r i dette punktet der r er dens krumningsradius. Den varierer vanligvis i størrelse fra punkt til punkt på kurven.[1]
Når kurven ikke ligger i et plan, vil krumningssirkelen generelt dreie seg fra punkt til punkt. Man sier derfor at kurven har en viss torsjon. Kurvens totale krumning er da bestemt både av denne og dens krumningsradius.
Beregning av krumning
Når en kurve i planet kan fremstilles ved en enkel funksjon y = f(x), er hvert punkt (x,y) på den gitt ved posisjonsvektoren r = x i + y j. tangentvektoren i samme punkt er nå gitt som den deriverte T = d r/dx = i + y' j. Her er y' = df /dx funksjonens stigningstall som gir kurvens helning med x-aksen. Desto raskere dette tallet varier langs kurven, desto større er krumningen.[1]
Forandringen må måles over en viss strekning gitt ved buelengden til kurven. For et lite stykke dx langs x-aksen vil kvadratet av denne forandringen være ds 2 = dx 2 + dy 2 som gir den spesifikke variasjonen
Man kan herav definere en normert tangentvektor t = T/|T| som oppfyller t⋅t = 1. Den er derfor gitt som
da det fra T = i + y' j følger at |T| = s' . Det er forandringen av denne vektoren som gir det kvantitative uttrykket for kurvens krumning. Den følger fra krumningsvektoren som er definert ved k = d t/ds. Lengden av den gir krumningen k = |k|. Den inverse verdien er krumningsradius r = 1/k.
Ved direkte utregning av den deriverte som opptrer i definisjonen av krumningsvektoren, finner man at resultatet kan skrives på formen
hvor |n| = 1. Koeffisienten her er derfor krumningen k til den plane kurven. Enhetsvektoren n peker fra punktet (x,y) til krumningssenteret og er
Den er normalen til kurven i punktet (x,y) og står vinkelrett på tangentvektoren t. Mens fortegnet til k er entydig, er retningen til normalen n avhengig av fortegnet man velger for krumningen.[2]
Krumning av flater

En flate har i det generelle tilfellet en krumning som kan beskrives ved Riemanns differensialgeometri. Dette er en utvidelse til høyere dimensjoner av differensialgeometrien som Gauss tidligere hadde utviklet spesielt for todimensjonal flater. I det tilfellet kan man tenke seg en normal som står vinkelrett på flaten i hvert punkt. Et plan gjennom normalen vil skjære flaten langs en kurve, og krumningen til denne kurven kan tas som et mål for flatens krumning. Ved dreining av snittplanet om normalen, vil den resulterende krumning i alminnelighet variere.[3]
For å gjøre dette mer kvantitativt, bestemmer man den største og den minste krumningen til slike snittkurver i ett og samme punkt. Disse kalles flatens hovedkrumninger k1 og k2 på dette stedet. De fremkommer for to retninger av snittplanet som står vinkelrett på hverandre.[2] Fra disse to verdiene kan man så bestemme dens middelkrumning (k1 + k2)/2 og dens intrinsikke krumning som er gitt ved produktet k1k2. Denne kalles også for flatens gaussiske krumning.
Hvis hovedkrumningene har motsatt fortegn, vil krumningen i hvert punkt på flaten gå i motsatte retninger som i en sadel. I det spesielle tilfellet at en av dem er null, vil det kunne legges en rett linje i den tilsvarende hovedretningen som på en sylinder. Men denne flaten sies likevel å være krummet da dens middelkrumning er forskjellig fra null.
Den intrinsikke krumningen skylder sitt navn at den kan bestemmes uten å måtte forlate flaten. For eksempel, på en kuleflate kan man flytte en vektor parallelt med seg selv fra ekvator til nordpolen langs en bestemt meridian. Hvis man så bringer den tilbake på samme måte til ekvator langs en annen meridian og videre der til utgangspunktet, vil den ha en litt annen retning enn hva den hadde før denne rundturen startet. Dreiningen av vektoren fra den opprinnelige retningen er nå et direkte uttrykk for krumningen til denne flaten.
Denne definisjonen av krumning kan også benyttes i rom med høyere dimensjoner. Der kan slike rundturer gjennomføres i flere retninger som generelt gir ulike resultat. Men disse kan inngå som komponentene til en multidimensjonal krumningstensor. Det er denne som benyttes i den generelle relativitetsteorien for beskrive krumningen av tidrommet.[4]
Referanser
- ^ a b R. Tambs Lyche, Matematisk Analyse I, Gyldendal Norsk Forlag, Oslo (1961).
- ^ a b D.J. Struik, Lectures on classical differential geometry, Dover Publications, New York (1961). ISBN 0-486-65609-8.
- ^ R. Tambs Lyche, Matematisk Analyse Bind II, Gyldendal Norsk Forlag, Oslo (1958).
- ^ C.W. Misner, K.S. Thorne and J.A. Wheeler, Gravitation, W. H. Freeman, San Francisco (1973). ISBN 0-7167-0344-0.
Eksterne lenker
- MIT, Principal normal and curvature, websider med forelesninger.



