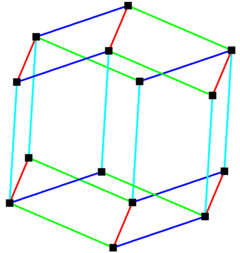
Dodecaedro rômbico
Na geometria, o dodecaedro rômbico é um poliedro convexo com 12 faces congruentes. Tem 24 arestas, e 14 vértices de dois tipos. É um sólido catalão,além de ser o poliedro dual do cuboctaedro.
Propriedades
O dodecaedro rômbico é um zonoedro. Seu poliedro dual é o cuboctahedron. A diagonal de cada face é exatamente √2 vezes o comprimento da diagonal menor, de modo que a face de ângulos agudos possui a medida de arccos 13, ou cerca de 70.53°.
Sendo o dual de um poliedro de Arquimedes, o dodecaedro rômbico é face-transitiva, ou seja, o grupo de simetria de um sólido transitivamente sobre o conjunto de faces. Nos termos fundamentais, isso significa que, para quaisquer duas faces A e B existe uma rotação ou reflexão do sólido que deixa de ocupar a mesma região do espaço ao mover-se face A para face B.
O dodecaedro rômbico é um dos nove poliedros aresta-transitivo convexos, sendo os outros cinco sólidos Platônicos, o cuboctahedron, o icosidodecaedro e o triacontaedro rômbico.
O dodecaedro rômbico pode ser usado para tesselar espaços tridimensionais. Pode ser empilhado para preencher um espaço muito parecido com hexágonos em um plano.
Este poliedro em um espaço de preenchimento tesselado, pode ser visto como a tesselação de Voronoi de face centrada cubic lattice. É a zona de Brillouin do cúbo de corpo centrado (bcc) em cristais. Alguns minerais, tais como granada formam um dodecaedro rômbico de cristais. As abelhas usam a geometria da forma centesimal do dodecaedro rômbico, a partir de um mosaico de células, cada uma das quais é um prisma hexagonal, cobertas com metade de um dodecaedro rômbico. O dodecaedro rômbico também aparece na unidade de células de diamante e diamantóides. Nestes casos, quatro vértices (suplente tríplice) estão ausentes, mas as ligações químicas escondem as arestas restantes arestas.[1]
O gráfico do dodecaedro rômbico é hamiltoniano.
Dimensões
Se o comprimento da aresta de um dodecaedro rômbico é um, o raio de uma esfera inscrita (tangente a cada um das faces do dodecaedro rômbico)
o raio da interesfera é
- .
e o raio da esfera circunscrita é
- .
Área e volume
A área A e o volume V do dodecaedro rômbico do comprimento da aresta são:
Projeções ortogonais
O dodecaedro rômbico tem quatro especais projeções ortogonais ao longo de seus eixos de simetria, centrada em uma face, uma aresta, e os dois tipos de vértices, triplo e quádruplo. Os dois últimos correspondem a B2 e2 plano de Coxeter.
simetria |
[4] | [6] | [2] | [2] |
|---|---|---|---|---|
| Dodecaedro rômbico |

|

|

|

|
| Cubotaedro (duplo) |

|

|

|

|
Coordenadas cartesianas
 Piritoedro variações entre um cubo e o dodecaedro rômbico |
 A expansão de um dodecaedro rômbicoc |
Os oito vértices, onde três faces encontram seus ângulos obtusos têm coordenadas Cartesianas:
- (±1, ±1, ±1)
As coordenadas dos seis vértices, onde quatro faces encontramm seus ângulos agudos são:
- (±2, 0, 0), (0, ±2, 0) e (0, 0, ±2)
O dodecaedro rômbico pode ser visto como um caso de limite degenerado de uma piritoédro, com permutação de coordenadas (±1, ±1, ±1) e (0, 1 + h, 1 − h2) com o parâmetro h = 1.
Formas topologicamente equivalente
Paraleloedro
O dodecaedro rômbico é um paraleloédro, um espaço de preenchimento de poliedro.
Outras construções simétricas do dodecaedro rômbico, são também espaço de preenchimento, e como paraleloédro são similares às variações do espaço de preenchimento truncado dos octaedros.[2]
Por exemplo, com 4 faces quadradas, e 60 graus faces rômbicas, e D4h diedro simetria, ordem 16. Ele será visto como um cubotaédro com pirâmides quadradas aumentadas na parte superior e inferior.
Dodecaédro Bilinski
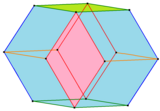 Dodecaedro Bilinski largura das arestas e faces frontais coloridas por sua simetria de posição. |
 Dodecaedro Bilinski pelas bordas paralelas coloridas |
Em 1960 Stanko Bilinski descobriu um segundo dodecaedro rômbico com 12 faces rômbicas congruentes, o dodecaedro Bilinski. Ele tem a mesma topologia, mas uma geometria diferente. O rômbico dessa forma tem a razão de ouro.[3][4]
| Primeira forma | Segunda forma |
|---|---|

|
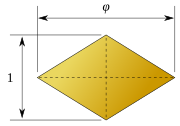
|
| √2:1 | √5 + 12:1 |
Dodecaedro trapezoidal

Outro variação topologicamente equivalentes, às vezes chamado de um dodecaedro trapezoidal, é isoedral com simetria tetraédrica ordem 24, distorcendo as faces rômbicas em "pipas". Tem 8 vértices, ajustados em conjuntos de 4, com o caso limite de uma tetraédrica envelope. Variações pode ser parametrizada por (a,b), onde b é determinada a partir de um para planar faces. (1,1) é a solução rômbica. Como (um) aproxima-se 12, (b) se aproxima do infinito.
- (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
- (a, a, a), (−a, −a, a), (−a, a, −a), (a, −a, −a)
- (−b, −b, −b), (−b, b, b), (b, −b, b), (b, b, −b)
Poliedros relacionados

Este poliedro é uma parte de uma seqüência de poliedros rômbicos e pavimentações com [n,3] simetria do grupo de coxeter. O cubo pode ser visto como um hexaedro rômbico onde o rombi são quadrados.
Da mesma forma ele se relaciona com a série infinita de pavimentações com as configurações da face V3.2n.3.2n, o primeiro no plano euclidiano, e o resto no plano hiperbólico.
 V3.4.3.4 |
 V3.6.3.6 |
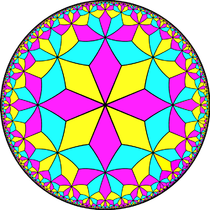 V3.8.3.8 |
Estrelamentos
Como muitos poliedros convexos, o dodecaedro rômbico pode ser estrelado estendendo as faces ou arestas até que elas se encontrem para formar um novo poliedro. Vários estrelamentos foram descritos por Dorman Lucas.[5]
O primeiro estrelamento, muitas vezes chamado simplesmente de o estrelado dodecaedro rômbico, é bem conhecido. Ele pode ser visto como um dodecaedro rômbico com cada face aumentada através da colocação de uma base de pirâmide rômbica, com uma altura de pirâmide tal que os lados encontram-se no plano das faces vizinhas:
Lucas descreve mais quatro estrelamentos: o segundo e o terceiro estrelamentos (expansão para fora), formada por remover o segundo, o terceiro, e outro, adicionando o rômbico dodecaedro original de volta para a anterior.
Grande dodecaedro rômbico : 12 faces côncavas ortogonais
Grande estrelado dodecaedro rômbico : 12 faces côncavas dodecagonais
Polítopos relacionados

A forma do casco dodecaedro rômbico do primeiro-vértice projeta de um tesserato de três dimensões. Há exatamente duas maneiras de decompor um dodecaedro rômbico em quatro paralelepípedos congruente, dando oito paralelepípedos possíveis. Oito células do tesserato sob esta projeção precisamente para estes oito paralelepípedos.
O dodecaedro rômbico, forma máxima seção transversal de uma 24-célula, e também faz o casco de seu projeção de primeiro-vértice paralela em três dimensões. O dodecaedro rômbico pode ser decomposto em seis congruentes (não-regular) bipiramide quadrada unindo em um único vértice no centro; estes formam as imagens dos seis pares da célula-24 das células octaédricas.As 12 células Octaédricas restantes projeta nas faces do dodecaedro rômbico. A não-regularidade destas imagens é devido a distorção projetada; as facetas da célula-24 são octaedros regulares de 4 dimensão.
Nesta decomposição é dado um método interessante método para construir o dodecaedro rômbico: cortar um cubo em seis congruentes pirâmides quadradas congruentes, e anexá-las para as faces de um segundo cubo. As faces triangulares de cada par adjacente da pirâmides estão sobre um plano, e então mesclar em paralelogramos. 24-célula pode também ser construído de uma forma análoga, usando dois tesseratos
Veja também
Referências
- ↑ Dodecahedral Crystal Habit Arquivado em 12 de abril de 2009, no Wayback Machine.. khulsey.com
- ↑ Order in Space: A design source book, Keith Critchlow, p.56–57
- ↑ Branko Grünbaum (2010). «The Bilinski Dodecahedron and Assorted Parallelohedra, Zonohedra, Monohedra, Isozonohedra, and Otherhedra» (PDF). 32 (4): 5–15. Consultado em 22 de março de 2017. Arquivado do original (PDF) em 2 de abril de 2015
- ↑ H.S.M Coxeter, "Regular polytopes", Dover publications, 1973.
- ↑ Luke, D. (1957). «Stellations of the rhombic dodecahedron». The Mathematical Gazette. 337: 189–194
Leia também
- Wenninger, Magnus. Dual Models. [S.l.: s.n.] ISBN 978-0-521-54325-5. MR 730208. doi:10.1017/CBO9780511569371 (Treze semiregular poliedros convexos e seus duplos, Página 19, Rhombic dodecaedro)
- As Simetrias de Coisas 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Capítulo 21, de Nomeação de Arquimedes e catalão poliedros e pavimentações, p. 285, Rhombic dodecaedro )
Ligações externas
- Realidade Virtual Poliedros – Enciclopédia de Poliedros
Modelos computacionais
- O relacionamento de uma Rhombic Triacontahedron e um Rhombic Dodecaedro, Rhombic Dodecaedro 5-Composto e Rhombic Dodecaedro 5-Composto por Sándor Kabai, O Projeto Wolfram Demonstrations.
Projetos de papel
- Calendário dodecaedro rômbico – faça uma calendário dodecaedro rômbico sem cola
- Outro Calendário dodecaedro rômbicoo feito por entrançar de tiras de papel
Aplicações práticas
- Instituto Arquimedes Exemplos de construção de habitação de projetos utilizando esta geometria