Espaço de Minkowski
Em física e matemática, espaço de Minkowski, também tratada de métrica de Minkowski, é a configuração matemática na qual a teoria da relatividade especial de Einstein é mais comumente formulada. Nessa configuração as três dimensões usuais do espaço são combinadas com uma única dimensão do tempo para formar uma variedade quadrimensional para representar um espaço-tempo.
O espaço de Minkowski possui este nome em referência ao matemático alemão Hermann Minkowski.
Estrutura
Formalmente, o espaço de Minkowski é um campo vetorial real quadrimensional equipado com uma forma bilinear simétrica, não degenerada, com assinatura (-,+,+,+).
Elementos do espaço de Minkowski são chamados eventos ou quadrivetores.
Espaço de Minkowski é frequentemente denotado R1,3 para enfatizar a assinatura, entretanto é também denotada M 4 ou simplesmente M.
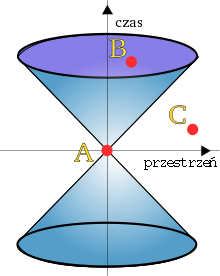
O Produto interno no espaço de Minkowski
O que se chama de produto interno no espaço de Minkowski é similar ao produto interno euclidiano, com uma diferença fundamental: enquanto que em um produto interno a equação v.v = 0 tem como única solução o vetor nulo v = 0, no caso do espaço de Minkowski existem vários quadrivetores que a satisfazem.
Este produto interno gera uma geometria diferente da euclideana, a geometria geralmente associada a relatividade.
Considere sendo um vetor-espaço real quadrimensional. O produto interno Minkowski é uma função (isto é, dado dois vetores quaisquer em define-se como um número real) que satisfaz as propriedades (1), (2), (3) listadas aqui, bem como a propriedade (4) dada abaixo:
1. bilinear: , ( e )
2. simétrica: ()
3. não degenerada: se , então ,
4. O produto interno tem assinatura métrica (-,+,+,+)












