Matriz Laplaciana
No campo matemático da teoria dos grafos, a matriz laplaciana, às vezes chamada matriz de admitância, matriz Kirchhoff ou laplaciano discreto, é uma representação matricial de um grafo . A matriz laplaciana pode ser usada para encontrar muitas propriedades úteis de um grafo. Juntamente com o teorema de Kirchhoff, ela pode ser usada para calcular o número de árvores de abrangência para um determinado grafo. O corte mais esparso de um grafo pode ser aproximado através do segundo menor autovalor de seu Laplaciano pela desigualdade de Cheeger . Também pode ser utilizada para construir incorporações de baixa dimensão, o que pode ser útil para uma variedade de aplicativos de aprendizado de máquina .
Definição
Matriz Laplaciana para grafos simples
Dado um grafo simples com vértices, sua matriz laplaciana é definida como: [1]
onde D é a matriz de graus e A é a matriz de adjacência do grafo. Uma vez que é um grafo simples, contém apenas 1s ou 0s e os seus elementos diagonais são todos 0s.
No caso de grafos direcionados, pode-se utilizar os graus de entrada ou os graus de saída, dependendo da aplicação.
Os elementos de são dados por
Onde é o grau do vértice .
Laplaciano simétrico normalizado
A matriz laplaciana simétrica normalizada é definida como: [1]
- ,
Os elementos de são dados por
Laplaciano normalizado de passeio aleatório
A matriz Laplaciana normalizada de percurso aleatório é definida como:
Os elementos de são dados por
Laplaciano generalizado
O Laplaciano generalizado é definido como [2] :
Observe que o Laplaciano comum é um Laplaciano generalizado.
Exemplo
Aqui está um exemplo simples de um grafo rotulado, não direcionado e sua matriz laplaciana.
| Grafo rotulado | Matriz de grau | Matriz de adjacência | Matriz laplaciana |
|---|---|---|---|
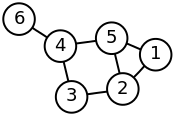
|
Propriedades
Para um grafo (não direcionado) G e sua matriz Laplaciana L com autovalores :
- L é simétrico.
- L é semidefinido positivo (ou seja, para todos ) Isso é verificado na seção da matriz de incidência (abaixo). Isso também pode ser visto pelo fato de o laplaciano ser simétrico e diagonalmente dominante .
- L é uma matriz M (suas entradas fora da diagonal não são positivas, mas as partes reais de seus autovalores são não-negativas).
- Cada soma de linha e de coluna de L é zero. De fato, na soma, o grau do vértice é somado com um "-1" para cada vizinho.
- Em consequência, , pois o vetor satisfaz Isso também implica que a matriz laplaciana é singular.
- O número de componentes conectados no grafo é a dimensão do espaço nulo do Laplaciano e a multiplicidade algébrica do autovalor 0.
- O menor autovalor não-nulo de L é chamado de gap espectral .
- O segundo menor autovalor de L (poderia ser zero) é a conectividade algébrica (ou valor de Fiedler ) de G e aproxima o corte mais esparso de um grafo.
- O Laplaciano é um operador no espaço vetorial n-dimensional de funções , Onde é o conjunto de vértices de G e .
- Quando G é um grafo regular de grau K, ou K-regular, o Laplaciano normalizado é: , onde A é a matriz de adjacência e I é uma matriz de identidade.
- Para um grafo com múltiplos componentes conectados, L é uma matriz diagonal de bloco, em que cada bloco é a respectiva matriz laplaciana de cada componente, possivelmente após reordenar os vértices (ou seja, L é semelhante à permutação de uma matriz diagonal de bloco).
- O traço da matriz laplaciana L é igual a onde é o número de arestas do grafo considerado.
Matriz de incidência
Defina uma matriz de incidência M orientada com elemento Mev de aresta e (vértices de ligação i e j, com i > j ) e vértice v dado por
Então a matriz laplaciana L satisfaz
Onde é a matriz transposta de M.
Agora considere uma autocomposição de , com autovetores de norma unitária e autovalores correspondentes :
pode ser escrito como o produto interno do vetor com ele próprio, isso mostra que e, portanto, os autovalores de são todos não negativos.
Laplaciano Deformado
O Laplaciano deformado é comumente definido como
onde I é a matriz unitária, A é a matriz de adjacência, D é a matriz de graus e s é um número (de valor complexo). O Laplaciano padrão é apenas . [3]
Laplaciano sem sinal
O Laplaciano sem sinal é definido como Onde é a matriz de graus e é a matriz de adjacência. [4] Como o Laplaciano assinado , o Laplaciano sem sinal também é semi-definido positivo, pois pode ser considerado onde é a matriz de incidência. tem um autovetor 0 se e somente se tiver um componente conectado bipartido que não seja vértices isolados. Isso pode ser mostrado como Isso tem uma solução onde se e somente se o grafo tiver um componente conectado bipartido.
Laplaciano normalizado simétrico
O Laplaciano normalizado (simétrico) é definido como
onde L é o Laplaciano (não normalizado), A é a matriz de adjacência e D é a matriz de graus. Como a matriz de graus D é diagonal e positiva, sua raiz quadrada recíproca é apenas a matriz diagonal cujas entradas diagonais são as recíprocas das raízes quadradas positivas das entradas diagonais de D. O Laplaciano normalizado simétrico é uma matriz simétrica.
Um deles tem: , em que S é a matriz cujas linhas são indexadas pelos vértices e cujas colunas são indexadas pelas arestas de G, de modo que cada coluna correspondente a uma aresta e = {u, v} tenha uma entrada na linha correspondente a u, uma entrada na linha correspondente a v e tenha 0 entradas em outro lugar. ( denota a transposição de S).
Todos os autovalores do Laplaciano normalizado são reais e não negativos. Podemos ver isso da seguinte maneira. Como é simétrico, seus autovalores são reais. Eles são também não negativos: considere um autovetor de com autovalor λ e suponha . (Podemos considerar g e f como funções reais nos vértices v. ) Então:
onde usamos o produto interno , uma soma sobre todos os vértices v, e denota a soma de todos os pares não ordenados de vértices adjacentes {u, v}. A quantidade é chamada de soma de Dirichlet de f, enquanto a expressão é chamada quociente de Rayleigh de g.
Seja 1 a função que assume o valor 1 em cada vértice. Então é uma autofunção de com autovalor 0. [5]
De fato, os autovalores do Laplaciano simétrico normalizado satisfazem 0 = μ 0 ≤… ≤ μ n − 1 ≤ 2. Esses autovalores (conhecidos como o espectro do Laplaciano normalizado) se relacionam bem com outros invariantes de grafos para grafos gerais. [6]
Laplaciano normalizado de passeio aleatório
O Laplaciano normalizado de passeio aleatório é definido como
onde D é a matriz de graus. Como a matriz de graus D é diagonal, sua inversa é simplesmente definida como uma matriz diagonal, com entradas diagonais que são as recíprocas das entradas diagonais positivas correspondentes de D.
Para os vértices isolados (aqueles com grau 0), uma escolha comum é definir o elemento correspondente para 0.
Esta convenção resulta em uma propriedade boa de que a multiplicidade do autovalor 0 é igual ao número de componentes conectados no grafo.
Os elementos matriciais de são dados por
O nome do Laplaciano normalizado de passeio aleatório provém do fato de que essa matriz é , onde é simplesmente a matriz de transição de um passeio aleatório no grafo. Por exemplo, deixe denotar o i-ésimo vetor da base canônica . Então é um vetor de probabilidade que representa a distribuição das localizações de um passeio aleatório após ter dado um único passo a partir do vértice ; ou seja, . De maneira mais geral, se o vetor é uma distribuição probabilística da localização de um passeio aleatório nos vértices do grafo, então é a distribuição probabilística do andador após passos.
Pode-se verificar que
- ,
ou seja, é semelhante ao Laplaciano normalizado . Por essa razão, mesmo que não é, em geral, hermitiana, ela possui autovalores reais. De fato, seus autovalores concordam com os de (que é hermitiana).
Grafos
Como um aparte sobre passeios aleatórios em grafos, considere um grafo simples e não direcionado . Considere a probabilidade de o andador estar no vértice i no tempo t, dada a distribuição de probabilidade de que ele estava no vértice j no tempo t-1 (assumindo uma chance uniforme de dar um passo ao longo de qualquer uma das arestas ligadas a um determinado vértice) :
ou em notação de vetor de matriz:
(O equilíbrio, que se estabelece em como , é definido por . )
Podemos reescrever essa relação como
é uma matriz simétrica chamada matriz de adjacência reduzida . Portanto, dar passos nesse passeio aleatório requer poderes de , que é uma operação simples porque é simétrica.
Interpretação com o operador de Laplace discreto
A matriz laplaciana pode ser interpretada como uma representação matricial de um caso particular do operador de Laplace discreto . Tal interpretação permite, por exemplo, generalizar a matriz laplaciana para o caso de grafos com um número infinito de vértices e arestas, levando a uma matriz laplaciana de dimensão infinita.
Suponha que descreve uma distribuição de calor através de um grafo, onde é o calor no vértice . De acordo com a lei de resfriamento de Newton, o calor transferido entre os nós e é proporcional a se os nós e estão conectados (se não estiverem conectados, nenhum calor será transferido). Então, para a capacidade calorífica ,
Na notação de vetor de matriz,
que dá
Observe que essa equação assume a mesma forma que a equação do calor, onde a matriz - L está substituindo o operador Laplaciano ; consequentemente, o "grafo Laplaciano".
Para encontrar uma solução para esta equação diferencial, aplique técnicas padrão para resolver uma equação diferencial matricial de primeira ordem. Ou seja, escreva como uma combinação linear de autovetores de L (para que ), com dependente do tempo.
Conectando-se à expressão original (porque L é uma matriz simétrica, seus autovetores de norma unitária ortogonais):
cuja solução é
- .
Como mostrado anteriormente, os autovalores de L são não-negativos, mostrando que a solução para a equação de difusão aproxima-se de um equilíbrio, pois apenas decai exponencialmente ou permanece constante. Isso também mostra que, dado um e a condição inicial , a solução em qualquer tempo t pode ser encontrada. [7]
Para encontrar para cada em termos da condição inicial geral , basta projetar nos autovetores de norma unitária ;
No caso de grafos não direcionados, isso funciona porque é simétrico e, pelo teorema espectral, seus autovetores são todos ortogonais. Portanto, a projeção sobre os autovetores de é simplesmente uma transformação de coordenadas ortogonais da condição inicial em um conjunto de coordenadas que decaem exponencialmente e independentemente umas das outras.
Comportamento de equilíbrio
Para entender , os únicos termos que restam são aqueles onde , uma vez que
Em outras palavras, o estado de equilíbrio do sistema é determinado completamente pelo núcleo de .
Uma vez que, por definição, , o vetor de valores 1 está no núcleo. Se houver componentes conexos disjuntos no grafo, então esse vetor de uns pode ser dividido na soma de autovetores independente de de uns e zeros, em que cada componente conexa corresponde a um autovetor com valores 1 nos elementos do componente conexo e zeros nos outros locais.
A conseqüência disso é que, para uma determinada condição inicial para um grafo com vértices
Onde
Para cada elemento de , ou seja, para cada vértice no grafo, ele pode ser reescrito como
- .
Em outras palavras, no estado estacionário, o valor de converge para o mesmo valor em cada um dos vértices do grafo, que é a média dos valores iniciais em todos os vértices. Como esta é a solução para a equação de difusão de calor, isso faz todo o sentido intuitivamente. Esperamos que os elementos vizinhos no grafo troquem energia até que essa energia seja distribuída uniformemente por todos os elementos que estão conectados entre si.
Exemplo do operador em uma grade
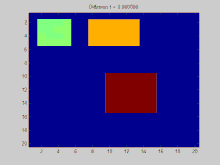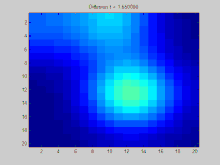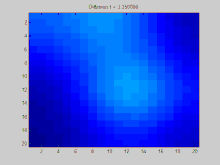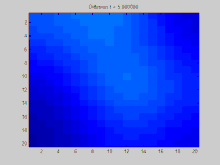
Esta seção apresenta um exemplo de uma função difundindo-se ao longo do tempo através de um grafo. O grafo neste exemplo é construído em uma grade 2D discreta, com pontos na grade conectados aos seus oito vizinhos. Três pontos iniciais são especificados para ter um valor positivo, enquanto o restante dos valores na grade são zero. Com o tempo, o decaimento exponencial atua para distribuir os valores nesses pontos uniformemente por toda a grade.
O código fonte completo do Matlab utilizado para gerar esta animação é fornecido abaixo. Ele mostra o processo de especificação das condições iniciais, projetando essas condições iniciais nos autovalores da Matriz Laplaciana e simulando o decaimento exponencial dessas condições iniciais previstas.
N = 20;%The number of pixels along a dimension of the image
A = zeros(N, N);%The image
Adj = zeros(N*N, N*N);%The adjacency matrix
%Use 8 neighbors, and fill in the adjacency matrix
dx = [-1, 0, 1, -1, 1, -1, 0, 1];
dy = [-1, -1, -1, 0, 0, 1, 1, 1];
for x = 1:N
for y = 1:N
index = (x-1)*N + y;
for ne = 1:length(dx)
newx = x + dx(ne);
newy = y + dy(ne);
if newx > 0 && newx <= N && newy > 0 && newy <= N
index2 = (newx-1)*N + newy;
Adj(index, index2) = 1;
end
end
end
end
%%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL
%%%EQUATION
Deg = diag(sum(Adj, 2));%Compute the degree matrix
L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices
[V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix
D = diag(D);
%Initial condition (place a few large positive values around and
%make everything else zero)
C0 = zeros(N, N);
C0(2:5, 2:5) = 5;
C0(10:15, 10:15) = 10;
C0(2:5, 8:13) = 7;
C0 = C0(:);
C0V = V'*C0;%Transform the initial condition into the coordinate system
%of the eigenvectors
for t = 0:0.05:5
%Loop through times and decay each initial component
Phi = C0V.*exp(-D*t);%Exponential decay for each component
Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system
Phi = reshape(Phi, N, N);
%Display the results and write to GIF file
imagesc(Phi);
caxis([0, 10]);
title(sprintf('Diffusion t = %3f', t));
frame = getframe(1);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if t == 0
imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);
else
imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
end
end
Aproximação ao Laplaciano contínuo negativo
A Matriz Laplaciana do grafo pode ainda ser vista como uma forma matricial de uma aproximação ao operador Laplaciano ( semidefinido positivo) obtido pelo método das diferenças finitas . (Veja equação discreta de Poisson) [8] Nesta interpretação, todo vértice do grafo é tratado como um ponto de grade; a conectividade local do vértice determina o estêncil da aproximação por diferença finita nesse ponto da grade, o tamanho da grade é sempre um para cada aresta e não há restrições em nenhum ponto da grade, o que corresponde ao caso da condição de fronteira de Neumann homogênea, ou seja, fronteira livre.
Multigrafos orientados
Um análogo da matriz laplaciana pode ser definido para multigrafos orientados. [9] Nesse caso, a matriz laplaciana L é definida como
onde D é uma matriz diagonal com D i, i igual ao grau de saída do vértice i e A é uma matriz com A i, j igual ao número de arestas de i a j (incluindo laços).
Veja também
- Matriz de rigidez
- Distância de resistência
- Matriz de taxa de transição
- Cálculo em grafos ponderados finitos
Referências
- T. Sunada, "Análise geométrica discreta", Proceedings of Symposia in Pure Mathematics, (ed. Por P. Exner, JP Keating, P. Kuchment, T. Sunada, A. Teplyaev), 77 (2008), 51-86.
- B. Bollobás, Modern Graph Theory, Springer-Verlag (1998, corrigido ed. 2013), ISBN 0-387-98488-7 , capítulos II.3 (Espaços vetoriais e matrizes associadas a gráficos), VIII.2 (Matriz de adjacência e o Laplaciano), IX.2 (Redes elétricas e passeios aleatórios).
[[Categoria:Matrizes]] [[Categoria:Grafos]] [[Categoria:!Páginas com traduções não revistas]]
Antevisão de referências
- ↑ a b Weisstein, Eric W. «Laplacian Matrix». MathWorld (em inglês)
- ↑ Godsil, C.; Royle, G. (2001). Algebraic Graph Theory, Graduate Texts in Mathematics. Springer-Verlag. [S.l.: s.n.]
- ↑ Morbidi (2013). «The Deformed Consensus Protocol» (PDF). Automatica. 49 (10): 3049–3055. doi:10.1016/j.automatica.2013.07.006
- ↑ Cvetković. «Towards a Spectral Theory of Graphs Based on the Signless Laplacian, III». Applicable Analysis and Discrete Mathematics. 4: 156–166. ISSN 1452-8630. JSTOR 43671298. doi:10.2298/AADM1000001C
- ↑ Chung, Fan R. K. (1997). Spectral graph theory. American Math. Soc. Repr. with corr., 2. [pr.] ed. Providence, RI: [s.n.] ISBN 978-0-8218-0315-8
- ↑ Chung, Fan (1997) [1992]. Spectral Graph Theory. American Mathematical Society. [S.l.: s.n.] ISBN 978-0821803158
- ↑ Newman, Mark (2010). Networks: An Introduction. Oxford University Press. [S.l.: s.n.] ISBN 978-0199206650
- ↑ Smola, Alexander J.; Kondor, Risi (2003), «Kernels and regularization on graphs», Learning Theory and Kernel Machines: 16th Annual Conference on Learning Theory and 7th Kernel Workshop, COLT/Kernel 2003, Washington, DC, USA, August 24–27, 2003, Proceedings, ISBN 978-3-540-40720-1, Lecture Notes in Computer Science, 2777, Springer, pp. 144–158, doi:10.1007/978-3-540-45167-9_12.
- ↑ «Matrix Tree Theorems». Journal of Combinatorial Theory, Series A. 24 (3): 377–381. 1978. ISSN 0097-3165. doi:10.1016/0097-3165(78)90067-5

















































































![{\displaystyle D^{-{\frac {1}{2}p(t)=\left[D^{-{\frac {1}{2}AD^{-{\frac {1}{2}\right]D^{-{\frac {1}{2}p(t-1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2439a87aff04e0e5afcead2752fe16a76967368c)













![{\displaystyle {\begin{aligned}{\frac {d\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)}{dt}+kL\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)&=0\\\sum _{i}\left[{\frac {dc_{i}{dt}\mathbf {v} _{i}+kc_{i}L\mathbf {v} _{i}\right]&=\\\sum _{i}\left[{\frac {dc_{i}{dt}\mathbf {v} _{i}+kc_{i}\lambda _{i}\mathbf {v} _{i}\right]&=\\{\frac {dc_{i}{dt}+k\lambda _{i}c_{i}&=0,\\\end{aligned}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5a67a61c17450a8864546cb7a35bcbff47d3ff)













![{\displaystyle \mathbf {v^{1} ={\frac {1}{\sqrt {N}[1,1,...,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e55a95330752e00904ca3160f9194a87ae62a522)


